Аналітичне подання кривих і поверхонь

Нехай на площині задана декартова система координат.

Крива на площині - це геометричне місце крапок 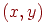, що задовольняють рівнянню

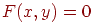
(4.10)

де - функція двох змінних. Ясно, що далеко не кожна функція буде задавати лінію. Так, наприклад, рівнянню

не задовольняє жодна крапка площини, а рівнянням

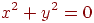
задовольняє тільки одна крапка .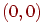

Для аналітичного подання кривої в багатьох випадках зручніше задавати криву параметричними рівняннями, використовуючи допоміжну змінну (параметр) :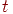

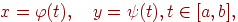
(4.11)

де 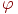й 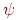- безперервні функції на заданому інтервалі зміни параметра. Якщо функція 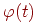така, що можна виразити 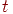через 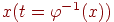, то від параметричного подання кривої легко перейти до рівняння (4.10):

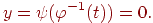
Систему рівнянь (4.11) можна записати у векторному виді:

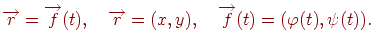
Відрізок прямої являє собою окремий випадок кривої, причому параметричне подання його може мати вигляд

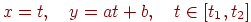
або

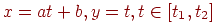
Окружність радіуса із центром у крапці 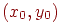може бути представлена параметричними рівняннями

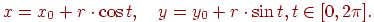
Перейдемо до тривимірного простору із заданої декартової системою координат.

Поверхня в просторі - це геометричне місце крапок 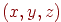, що задовольняють рівнянню виду

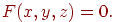
(4.12)

Так само як і у випадку кривої на площині, не всяка функція описує яку-небудь поверхню. Наприклад, рівнянню

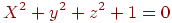
не задовольняє жодна крапка простору. Поверхня також може бути задана в параметричному виді, але на відміну від кривої для цього потрібні два допоміжні змінні (параметри):

(4.13)

Наприклад, сфера радіуса 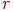із центром у крапці 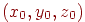може бути задана рівнянням

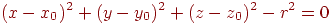
або ж параметричними рівняннями

Криву в просторі можна описати як перетинання двох поверхонь, тобто за допомогою системи рівнянь

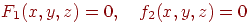
(4.14)

або параметричними рівняннями виду

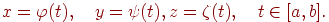
(4.15)