Системи координат і вектори

Для подальшого викладу нам знадобляться деякі відомості з аналітичної геометрії й лінійної алгебри. Не ставлячи перед собою завдання докладного розгляду всіх цих питань, приведемо (або нагадаємо) ті основні поняття й операції, які використовуються в алгоритмах комп'ютерної графіки.

Дві взаємно перпендикулярні пересічні прямі із заданим масштабом утворять декартову прямокутну систему координат на площині. Крапка перетинання O називається початком координат, прямі називаються осями координат. Одну з осей називають віссю OX, або віссю абсцис, іншу - віссю OY, або віссю ординат. Ці осі також називають координатними осями.

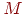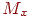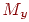Візьмемо довільну крапку на площині із заданою системою координат. Нехай і - проекції цієї крапки на осі абсцис і ординат відповідно, причому довжина відрізка 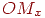дорівнює 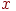, а довжина 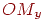дорівнює 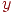. Тоді пари чисел 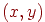називається декартовими координатами крапки 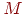на площині (абсцисою й ординатою крапки).

Три взаємно перпендикулярні пересічні прямі із заданим масштабом утворять декартову прямокутну систему координат у просторі. Так само як і у випадку площини, крапка перетинання O називається початком координат, прямі називаються осями координат. Одну з осей називають віссю OX, або віссю абсцис, іншу - віссю OY, або віссю ординат, третю - віссю OZ, або віссю аплікат.

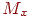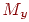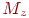Нехай , і - проекції довільної крапки 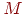в просторі на осі абсцис, ординат і аплікат відповідно, причому довжина відрізка 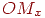дорівнює 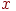, довжина 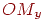дорівнює 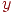, а дліна 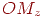дорівнює 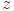. Тоді трійка чисел 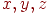називається декартовыми координатами крапки в просторі (абсцисою, ординатою й аплікатою крапки).

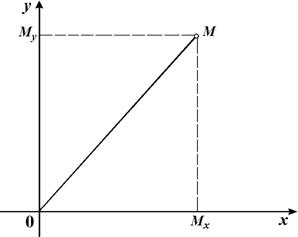
Рис. 4.1. Система координат на площині

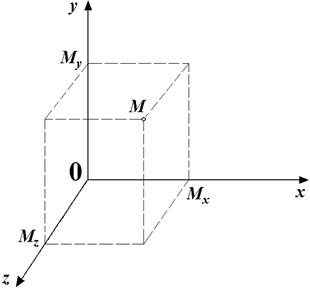
Рис. 4.2. Система координат у просторі

Нехай на площині задана декартова система координат. Візьмемо дві крапки з координатам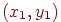и й 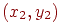відповідно. Тоді, використовуючи терему Піфагора, можна одержати, що відстань між цими двома крапками виражається формулою

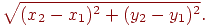
Відстань між двома крапками в просторі з координатам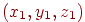и й 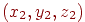виражається аналогічною формулою:

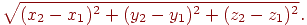
Відрізок на площині й у просторі задається за допомогою двох крапок, що вказують його границі. Геометричним вектором, або просто вектором у просторі, будемо називати відрізок, у якого зазначено, яка з його граничних крапок є початком, а яка - кінцем (тобто зазначений напрямок вектора). Початок вектора називають крапкою його додатка. Вектор називається нульовим, якщо його початок і кінець збігаються. Вектори називаються колінеарними, якщо вони лежать на паралельних прямих. Вектори вважаються рівними, якщо вони колінеарни, мають однакову довжину й однаковий напрямок. Таким чином, всі вектори, що виходять паралельним переносом з того самого вектора, рівні мeжду собою. Будь-яка крапка на площині й у просторі може розглядатися як вектор, початок якого збігається з початком координат ( радіус-вектор), а кожний вектор, перенесений у початок координат, задає своїм кінцем єдину крапку простору. Тому будь-який вектор може бути представлений сукупністю своїх координат у декартовій системі.

Лінійними операціями над векторами прийнято називати операції додавання векторів і операцію множення вектора на число.

Сумою двох векторів 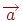і 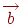називається вектор, що йде з початку вектора 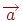в кінець вектора 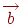, за умови, що вектор 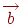прикладений до кінця вектора .

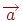Перелічимо основні властивості операції додавання векторів:

-

-

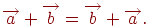
- Існує нульовий вектор 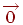, такий, що 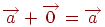для будь-якого вектора .

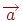- Для кожного вектора 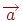існує протилежний йому вектор 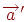, такий, що .

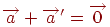Різницею двох векторів 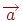і 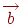називається такий вектор 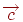, що у сумі з вектором 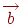дає вектор .

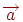Добутком вектора 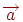на число 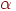називається вектор 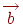, колінеарний вектору 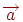, що має довжину 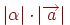й напрямок, що збігається з напрямком вектора 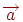при й протиставлене напрямку 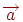при 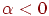. Геометричний зміст множення вектора на число полягає в тому, що довжина вектора збільшується в 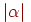раз.

Операція множення вектора на число має наступні властивості:

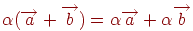- (розподільна властивість числового співмножника щодо суми векторів);

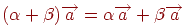- (розподільна властивість векторного співмножника щодо суми чисел);

- (сполучна властивість числових співмножників);

- якщо вектор 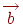колінеарен ненульовому вектору 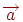, то існує речовинне число 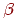, таке, що .

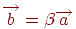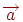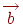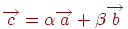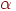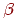Лінійною комбінацією векторів і називається вектор . При цьому числа й називаються коефіцієнтами розкладання вектора 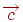по векторах 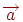і .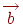

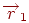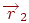Якщо два вектори й задані своїми координатам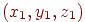и й 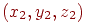, то операції над ними легко виразити через ці координати:

-

-

-

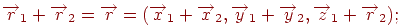
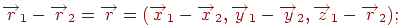
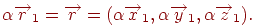
Вектори 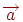, 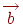і 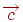називаються компланарними, якщо вони лежать в одній площині.

Вектори називаються лінійно незалежними, якщо рівність нулю їхньої лінійної комбінації можливо тільки у випадку рівності нулю коефіцієнтів 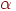і .

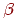Справедливі наступні властивості:

- Які б не були неколінеарні вектор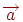и й 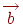, для будь-якого вектора 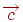, що лежить в одній площині з ними, існують числа 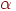й 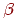, такі, що 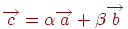, причому така пари чисел для кожного вектора єдина. Таке подання вектора 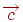називається розкладанням по векторах 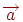і .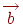

- Які б не були некомпланарні вектори 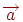, 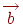і 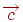, для будь-якого вектора 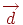існують числа 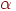, 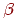і 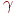, такі, що 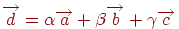, причому ця трійка чисел для кожного вектора - єдинийственная (розкладання вектора 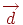по векторах ).

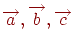- Будь-які три вектори в системі координат площини є лінійно залежними.

- Будь-які чотири вектори в системі координат простори є лінійно залежними.

Говорять, що пари лінійно незалежних векторів на площині (трійка лінійно незалежних векторів у просторі) утворять базис, оскільки будь-який вектор може бути представлений у вигляді лінійної комбінації цих векторів. Коефіцієнти розкладання вектора по базисних векторах називаються координатами вектора в цьому базисі. Якщо вектори базису взаємно перпендикулярні й мають одиничну довжину, то базис називається ортонормованим, а вектори базису називаються ортами. Таким чином, базис із одиничних векторів, спрямованих уздовж осей декартової системи координат, є ортонормованим.

Скалярним добутком векторів 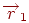і 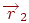називається число, рівне добутку довжин цих векторів на косинус кута між ними. Будемо позначати скалярний добуток векторів символом 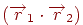. Тоді скалярний добуток можна виразити формулою

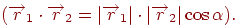
Нескладно довести наступні властивості даної операції.

- Скалярний добуток двох ненульових векторів дорівнює нулю тоді й тільки тоді, коли ці вектори ортогональни.

- Якщо кут між двома векторами гострий, то скалярний добуток цих векторів позитивно, якщо ж кут тупий, те скалярний добуток негативно.

- (властивість комутативності).

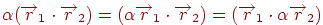- (сполучне щодо числового множника властивість).

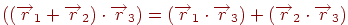- (розподільне щодо суми векторів властивість).

- Скалярний добуток вектора самого на себе дорівнює квадрату довжини вектора.

Приведемо деякі формули, пов'язані з розкладанням вектора в декартовій системі координат.

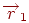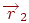Нехай вектори й задані своїми координатам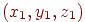и й 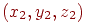. Тоді їхній скалярний добуток може бути обчислене по формулі

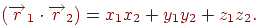
(4.1)

Звідси треба умова перпендикулярності векторів:

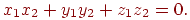
І, нарешті, косинус кута між векторами обчислюється по формулі

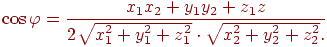
(4.2)

Тепер відстань між двома крапками з координатам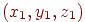и й 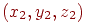можна виразити через скалярний добуток відповідних векторів:

Уведемо ще одне поняття, що стосується векторів. Три вектори називаються впорядкованою трійкою, якщо зазначено, який із цих векторів є першим, який - другим і який - третім. При записі трійки векторів будемо розташовувати ці вектор у порядку їхнього проходження. Так, запис 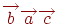означає, що першим вектором трійки є вектор 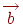, другим - 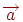, третім - .

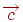Трійка векторів називається правої (лівої), якщо після приведення до загального початку вектор 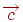розташовується по ту сторону від площини, що містить вектори 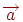, , 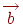звідки найкоротший поворот від 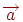до 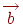здаєтьсяпроти годинникової стрілки (за годинниковою стрілкою).

Векторним добутком вектора 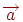на вектор 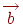називається вектор 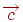, позначуваний символом 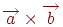і задовольняючою наступною вимогами:

- довжина вектора 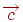дорівнює добутку довжин векторів 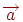, 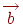на синус кута між ними, тобто

-

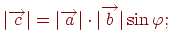
- вектор 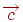ортогонален векторам , ;

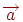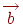- вектор 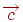спрямований так, що трійка векторів є правою.

Приведемо (без доказу) основні властивості векторного добутку.

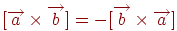- (антисиметричність);

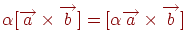- (сполучна властивість щодо множення на число);

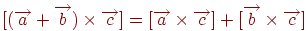- (розподільна властивість щодо додавання);

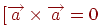- для будь-якого вектора .

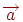Ясно, що векторний добуток двох колінеарних векторів дає нульовий вектор. Виведемо тепер формулy для векторного добутку. Нехай базисні вектори декартової системи координат 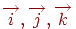утворять праву трійку. Тоді справедливі наступні співвідношення:

Якщо задані два вектор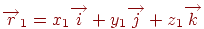и й 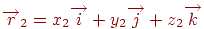, те, з огляду на властивості векторного добутку, звідси легко вивести, що

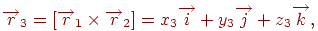
де

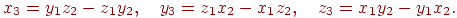
(4.3)