Перехід в іншу систему координат
Ми розглянули перетворення геометричних об'єктів, заданих у певній декартовій системі координат. Але в багатьох випадках зручно розглядати ті ж об'єкти в іншій системі координат, оскільки їхній опис може стати більше простим. Найпростіший приклад - завдання координат паралелепіпеда: простіше всього це зробити в системі координат, сполученої з однієї з його вершин з осями, спрямованими уздовж ребер. У зв'язку із цим зупинимося на питанні, як зміняться координати крапки при переході від однієї декартової системи координат до іншої.
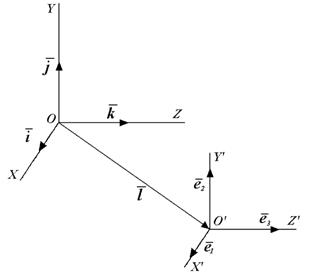
Рис. 4.9. Дві системи координат у просторі
Нехай одиничні орти першої системи координат позначаються 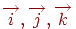 , а осі координат -
, а осі координат - 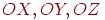 . Уведемо ще одну систему координат, одиничні орти якої позначимо
. Уведемо ще одну систему координат, одиничні орти якої позначимо  , а осі координат -
, а осі координат - 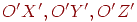 . Ця система має свій початок координат і свої напрямки осей. Уважаємо, що в обох системах координат орти утворять праву трійку (мал. 4.9).
. Ця система має свій початок координат і свої напрямки осей. Уважаємо, що в обох системах координат орти утворять праву трійку (мал. 4.9).
Спочатку розглянемо ситуацію, коли крапка 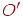 збігається із крапкою
збігається із крапкою  . Вектори
. Вектори  можна задати в першій системі координат, розклавши їх по векторах
можна задати в першій системі координат, розклавши їх по векторах 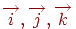 :
:

Якщо в першій системі крапка 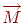 має координати
має координати 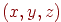 , а в другій системі -
, а в другій системі -  , те, мабуть,
, те, мабуть,
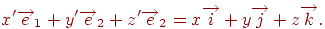
Множачи скалярно це співвідношення на вектори  , одержимо зв'язок між значеннями координат у різних системах:
, одержимо зв'язок між значеннями координат у різних системах:
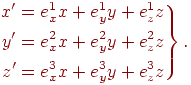
Ці співвідношення можна записати в матричному виді
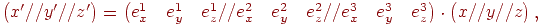
| (4.11) |
або у векторному записі

Припустимо, що друга система координат отримана з першої шляхом повороту на кут 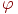 щодо осі
щодо осі 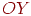 . Тоді
. Тоді

отже
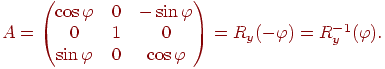
Таким чином, при поворотах системи координат нові координати крапок виходять шляхом множення матриці повороту на протилежний кут на вектор вихідних координат.
Якщо нова система координат отримана зі старої шляхом зрушення на вектор 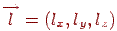 , то очевидно, що нові координати крапки задаються формулами
, то очевидно, що нові координати крапки задаються формулами
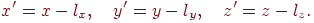
Тепер можна розглянути композицію двох перетворень системи координат - переносу й обертання. Тоді координати крапок перетворяться по формулі
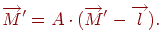
| (4.12) |
Дата добавления: 2015-04-03; просмотров: 1139;
