Полігональні моделі

Для цих просторових моделей використовуються як примітиви вершини (крапки в просторі), відрізки прямих (вектори), з яких будуються полілінії, полігони й полігональні поверхні. Головним елементом опису є вершина, всі інші є похідними. У тривимірної декартовій системі координати вершини визначаються своїми координатами (x,y,z), лінія задається двома вершинами, полілінія являє собою незамкнуту ламану лінію, полігон - замкнуту ламану лінію. Полігон моделює плоский об'єкт і може описувати плоску грань об'ємного об'єкта. Кілька граней становлять цей об'єкт у вигляді полігональної поверхні - багатогранник або незамкнута поверхня ("полігональна сітка").

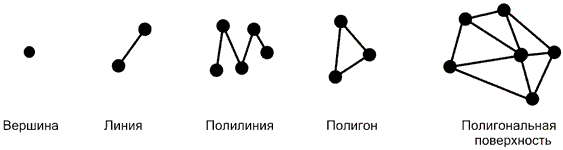
Рис. 5.1. Полігональні моделі

У сучасній комп'ютерній графіці векторно-полігональна модель є найпоширенішою. Вона застосовується в системах автоматизованого проектування, комп'ютерних іграх, тренажерах, ГИС, САПР і т.д. Достоїнства цієї моделі полягають у наступному:

- Зручність масштабування об'єктів.

- Невеликий обсяг даних для опису простих поверхонь.

- Апаратна підтримка багатьох операцій.

До числа недоліків полігональних моделей можна віднести те, що алгоритми візуалізації виконання топологічних операцій (наприклад, побудова перетинів) досить складні. Крім того, апроксимація плоскими гранями приводить до значної погрішності, особливо при моделюванні поверхонь складної форми.