Однорідні координати. Завдання геометричних перетворень в однорідних координатах за допомогою матриць

У попередній главі описувалися геометричні перетворення на площині й у просторі, а також було показано, як можна використовувати апарат матриць для таких завдань. Для перетворень на площині застосовувалися двовимірні вектори й матриці розмірністю 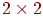. У просторі, відповідно, із цією же метою використовувалися тривимірні вектори й матриці 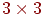. Але такий підхід не дозволяє задавати за допомогою матриць перетворення переносу й проекції. У зв'язку із цим у проективній геометрії був розроблений апарат, що дозволяє уніфікувати всі геометричні перетворення шляхом введення так званих однорідних координат.

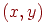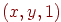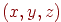Для пояснення такого підходу спочатку розглянемо випадок двовимірного простору. Кожна крапка площини з координатами може одночасно розглядатися як крапка тривимірного простору з координатами , тобто як крапка, що лежить на площині . З іншого боку, кожній крапці тривимірного простору за умови 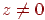відповідає єдина крапка цієї ж площини 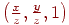. При цьому виходить, що кожній крапці площини 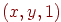відповідає пряма, що проходить через початок координат, тобто встановлюється взаємно однозначна відповідність між крапками площини й безлічами .

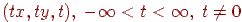Якщо тепер розглядати крапку площини як приналежному тривимірному простору, то її двовимірні перетворення можна буде описувати за допомогою матриць 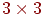, причому можна буде задавати таким способом не тільки повороти й масштабування, але й зрушення й проекції (як ортографичні, так і центральні).

Поворот на кут 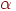відносно початку координат можна здійснити за допомогою нової матриці повороту:

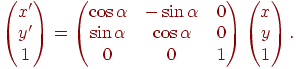
Операція масштабування може бути записана у вигляді

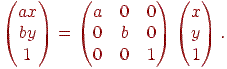
Перенос на вектор 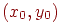також можна задати за допомогою матриці:

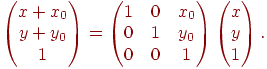
Проекції крапки на осі координат визначаються за допомогою матриць проекції:

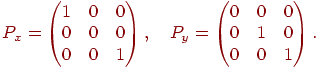
Перейдемо тепер до тривимірного простору. Кожній крапці 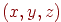будемо ставити у відповідність крапку чьотирьохмірного простору 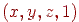, а для виконання основних перетворень будемо використовувати матриці розмірністю 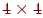. Будуються вони зовсім аналогічно тому, як це робилося у двовимірному випадку. Матриця зрушення на вектор 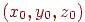має вигляд

матриця масштабування теж очевидним образом будується із тривимірної матриці:

Проекції крапок на координатні площини здійснюються за допомогою матриць (більш докладно проекції і їхніх видів будуть розглянуті пізніше):

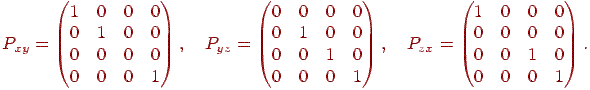
Множення цих матриць на вектор приводить до того, що обнулюється одна з координат, і в результаті одержуємо проекцію крапки на відповідну площину.

Матриця повороту щодо осі 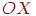на кут 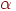виглядає в такий спосіб:

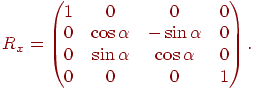
Звідси легко зрозуміти, як будуються матриці повороту щодо інших координатних осей, а також матриця повороту щодо довільної осі. Просто беремо матриці, побудовані в третьому розділі, і розширюємо їх шляхом додавання вже відомих одиничних вектора-рядка й вектора- стовпця:

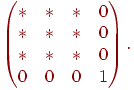
Шляхом об'єднання наведених елементарних перетворень можна побудувати й більше складні. У третьому розділі ми використовували добуток простих матриць обертання для побудови матриці повороту щодо довільної осі. Приведемо один приклад.

Нехай у просторі задані два відрізки - 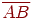і . Будемо будувати матрицю перетворення, що переводить перший відрізок у другий. Це перетворення розкладемо на наступні елементарні дії.

1. Зрушення, що переміщає крапку 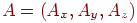в крапку .

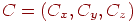2. Зрушення початку координат у цю же крапку.

3. Якщо відрізки неколінеарні:

- будується вектор нормалі до площини, у якій лежать відрізки (для цього можна використовувати векторний добуток вихідних векторів);

- поворот щодо вектора нормалі, що сполучає два відрізки по напрямку (кут повороту можна визначити за допомогою скалярного добутку вихідних векторів).

4. Масштабування з метою вирівнювання довжини відрізків.

5. Повернення початку координат у вихідну точку.

Кожне із цих перетворень реалізується за допомогою матриці, а повне перетворення можна виконати, використовуючи добуток матриць.

Використання матриць дуже зручно для виконання перетворень у просторі, хоча в деяких випадках це приводить до надлишкового числа виконуваних операцій. Наприклад, поворот однієї крапки в просторі щодо координатної осі за допомогою матриць в однорідних координатах вимагає 16 операцій множення й 12 операцій додавання. У той же час він легко може бути виконаний за допомогою формул перетворення

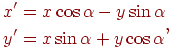
т.е. за допомогою всього лише чотирьох множень і одного додавання й одного вирахування. Операції зрушення також набагато більш економічно виконувати без використання матриць. Але коли мова йде про суперпозицію багатьох перетворень (як, наприклад, у випадку повороту щодо довільної осі), те доцільно застосовувати відповідну матрицю повороту. Ефективність матричного підходу дуже сильно зростає, якщо матричні операції реалізовані апаратно. Питання про те, у яких випадках використовувати матриці, а в яких ні, багато в чому залежить від можливостей обчислювальної техніки, рівня складності завдання й вимог до тимчасових характеристик процесу візуалізації.

Питання й вправи

1. Які геометричні об'єкти вважаються примітивами?

2. Які вимоги пред'являються до набору геометричних примітивів?

3. У якій програмі вперше як геометричний примітив використовувався прямокутник?

4. Що таке об'єктна система координат?

5. Що таке система координат спостерігача?

6. Чи відповідають розміри об'єктів у системі координат спостерігача їхнім реальним розмірам?

7. Що таке картинна площина?

8. Як називається операція переходу від тривимірної системи координат до двовимірного?

9. Що відбувається при перенесенні зображення з картинної площини на екран?

10. Чим відрізняються однорідні координати крапки від звичайних декартових координат?

11. З якою метою вводяться однорідні координати?

12. Скільки елементарних дій потрібно для сполучення двох відрізків у просторі?

13. Чи завжди використання матриць для виконання перетворень у просторі ефективніше, ніж інші способи їхньої реалізації?