Воксельні моделі

Воксельна модель - це подання об'єктів у вигляді тривимірного масиву об'ємних (кубічних) елементів. Сама назва "воксель" складено із двох слів: volume element. Так само як і піксель, воксель має свої атрибути (колір, прозорість і т.п.). Повна прозорість вокселя означає порожнечу у відповідній крапці обсягу. Чим більше вокселів у певному обсязі й менше їхній розмір, тим точніше моделюються тривимірні об'єкти.

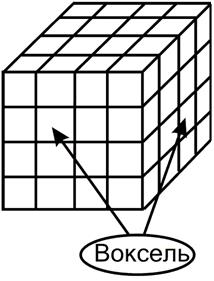
Рис. 5.2. Воксельна модель

Позитивними рисами воксельної моделі є:

- Можливість представляти внутрішність об'єкта, а не тільки зовнішній шар; проста процедура відображення об'ємних сцен.

- Просте виконання топологічних операцій; наприклад, щоб показати перетин просторового тіла, досить вокселі зробити прозорими.

До її недоліків ставляться:

- Велика кількість інформації, необхідне для подання об'ємних даних.

- Значні витрати пам'яті, що обмежують розв'язну здатність, точність моделювання.

- Проблеми при збільшенні або зменшенні зображення; наприклад, зі збільшенням погіршується розв'язна здатність зображення.

Поверхні вільних форм (функціональні моделі)

Характерною рисою пропонованого способу завдання поверхонь є те, що основним примітивом тут є поверхня другого порядку - квадрик. Він визначається за допомогою речовинної безперервної функції трьох змінних 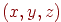у вигляді нерівності

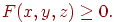
Таким чином, квадрик є замкнута підмножина евклідова простору, всі крапки якого задовольняють зазначеній нерівності. Рівняння

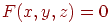
описує границю цієї безлічі. Безліч крапок, що задовольняють нерівності

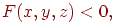
утворить зовнішню область квадрика.

Вільна форма - це довільна поверхня, що володіє властивостями гладкості, безперервності й нерозривності. На базі квадриков будуються вільні форми, які описують функціональні моделі. Вільна форма, побудована на цих принципах, має ряд достоїнств, до яких, у першу чергу, треба віднести наступні:

- Легка процедура розрахунку координат кожної крапки.

- Невеликий обсяг інформації для опису досить складних форм.

- Можливість будувати поверхні на основі скалярних даних без попередньої тріангуляції.

Цей підхід буде більш докладно викладений у наступних главах.

У нашім курсі передбачається розглянути растрові алгоритми для зображення таких геометричних примітивів, як відрізки, багатокутники, окружності й еліпси. Але спочатку ми займемося тим геометричним апаратом, що дозволить адекватно описувати об'єкти в просторі, працювати з ними й формувати зображення.