Общее уравнение Шредингера

Рассмотрим свободно движущуюся частицу. Согласно теории де Бройля ей можно сопоставить плоскую волну, описываемую уравнением

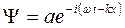(22.5.1.)

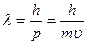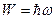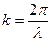Учитывая, что длина волны де Бройля и энергия и - волновое число придем к выражению

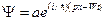(22.5.2)

Продифференцировав выражение (22.5.2) один раз по t, а второй раз дважды по х, получим

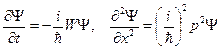
Отсюда

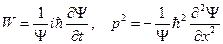
В нерелятивистской классической механике кинетическая энергия W и импульс р свободной частицы связаны соотношением

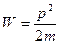
Подставив в это соотношение выражения для W и р² получим уравнение

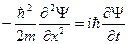, (22.5.3.)

которое совпадает с временным уравнением, если предположить, что потенциальная энергия U = 0.

В случае частицы, движущейся в силовом поле, характеризуемом потенциальной энергией U, кинетическая энергия W и импульс р связаны соотношением

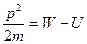
получим

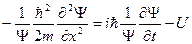(22.5.4.)

Умножив соотношение (22.5.4.) на Ψ придем к уравнению

,

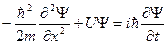соответствующего общему уравнению Шредингера.

Основными задачами квантовой механики являются:

1. Поведение свободной частицы

2. Поведение частицы в потенциальной яме или с бесконечно высокими стенками

3. Прохождение частицы через потенциальный барьер (туннельный эффект)

4. Квантовый гармонический осциллятор.

Более подробно рассмотрим задачу о движении свободной частицы.