Соотношение неопределенности Гейзенберга для: координат и импульса, энергии и времени. Невозможность одновременного измерения двух величин в квантовой физике.
Волновые свойства микрочастиц вносят ограничения в возможность применять к таким частицам понятия координаты и импульса в их классическом смысле. Например, электрон (и любая другая микрочастица) не может иметь одновременно точных значений координаты x и компоненты импульса рх. Неопределенности значений x и рх удовлетворяют соотношению:
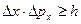
неопределенность импульса вдоль осей у и z соответственно равны:
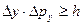
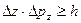
 |
Данные соотношения называются соотношения неопределенностей Гейзенберга. В этих уравнениях Δх, Δy, Δz означают интервалы координат, в которых может быть локализована частица, описываемая волной де Бройля, если проекция ее импульса по осям координат заключены в интервалах Δрх, Δрy, Δрz соответственно.
Определим значение координаты х свободно летящей микрочастицы, поставив на ее пути щель ширины Δх, расположенную перпендикулярно к направлению движения частицы (рис.22.1). Так как частица обладает волновыми свойствами света, то при прохождении через щель, размер которой сравним с длиной волны де Бройля частицы, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране, характеризуется главным максимумом, расположенным симметрично оси у и побочными максимумами по обе стороны от главного (мы их рассматривать не будем, т.к. основная доля интенсивности приходится на главный максимум).
До прохождения частицы через щель частица двигалась вдоль оси у, поэтому составляющая импульса рх =0 и Δрх = 0, а координата х частицы является совершенно неопределенной. В момент прохождения частицы через щель положение в направлении оси Х определяется с точностью до ширины щели, т.е. с точностью до Δх. В этот же момент вследствие дифракции частица отклонится от первоначального угла φ, соответствующий первому дифракционному максимуму, и будет двигаться в пределах угла 2φ. Следовательно, появится неопределенность в значении составляющей импульса частицы вдоль оси Х, которая как видно из рисунка равна:

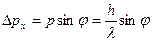
Из теории дифракции известно, что первый минимум соответствует углу φ, соответствующей условию
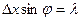
где Δх – ширина щели, λ – длина волны де Бройля.
Следовательно, получим
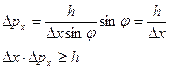
- соотношение неопределенности Гейзенберга. В этом уравнение было учтено, что у некоторых частиц, попадающих за пределы главного максимума, величина 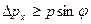 . Невозможность одновременно точно определить координату и соответствующую проекцию импульса, не связана с несовершенством методов измерения или измерительных приборов, а является следствием двойственной корпускулярно-волновой природы микрообъектов. Соотношение неопределенностей было получено с использованием одновременно классических характеристик движения частицы (импульс, координата) и наличия у нее волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей Гейзенберга является квантовым ограничением применимости классической механики к микрообъектам.
. Невозможность одновременно точно определить координату и соответствующую проекцию импульса, не связана с несовершенством методов измерения или измерительных приборов, а является следствием двойственной корпускулярно-волновой природы микрообъектов. Соотношение неопределенностей было получено с использованием одновременно классических характеристик движения частицы (импульс, координата) и наличия у нее волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей Гейзенберга является квантовым ограничением применимости классической механики к микрообъектам.
Соотношение неопределенностей энергии Е и времени t:
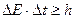 .
.
где ΔЕ – неопределенность энергии частицы, которая находится в течение времени Δt в состоянии с энергией Е. Энергия частицы в данном состоянии может быть определена тем точнее, чем дольше частица находится в этом состоянии.
Дата добавления: 2015-04-19; просмотров: 1389;
