Теплоемкость газов. Уравнение Майера.
Теплоемкость идеального двухатомного газа.
Теплоемкостью системы тел (тела) называется физическая величина, равная отношению количества теплоты dQ, которое нужно затратить для нагревания системы тел (тела), к изменению температуры dТ, характеризующей это нагревание:
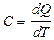 . [C]=Дж/К.
. [C]=Дж/К.
Удельной теплоемкостью вещества с называется скалярная величина, равная отношению теплоемкости однородного тела С к его массе:
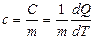 . [c]= Дж/(кг.К) (9.3.1)
. [c]= Дж/(кг.К) (9.3.1)
Молярной теплоемкостью называется физическая величина, численно равная отношению теплоемкости системы С к количеству вещества n, содержащегося в ней:
 . [Cm]=Дж/(моль.К) (9.3.2)
. [Cm]=Дж/(моль.К) (9.3.2)
Различают молярные теплоемкости при постоянном объеме СV и постоянном давлении Cp:
 ;
; 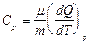 . (9.3.3)
. (9.3.3)
Уравнение, связывающее молярные теплоемкости при постоянном давлении и постоянном объеме имеет вид (уравнение Майера):
Cp – CV= R, (9.3.4)
где R – универсальная газовая постоянная.
Учитывая распределение энергии по степеням свободы и уравнение Майера (9.3.4), получим распределение теплоемкостей Cp и CV по степеням свободы:

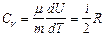 ,
,
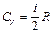 ,
, 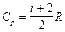 .
.
При рассмотрении термодинамических процессов удобно пользоваться соотношением:  .
.
Величина g - показатель адиабаты - определяется числом и характером степеней свободы молекулы (табл.1).
Таблица 1.
| Молекула | Число степеней свободы | CV | Cp | g | ||
| Поступательное движение | Вращательное движение. | i | ||||
| Одноатомная | - | 
| 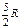
| 1,67 | ||
| Двухатомная | 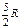
| 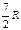
| 1,40 | |||
| Трехатомная | 3R | 4R | 1,33 |
Обратимся к двухатомной молекуле. Если связь между атомами жесткая, то число степеней свободы равна 5 (три поступательных и две вращательных). Теперь предположим, что связь упругая, то есть атомы могут совершать колебания друг относительно друга. Тогда требуется еще одна координата для определения конфигурации молекулы, это расстояние между атомами. Следовательно, у двухатомной молекулы в общем случае шесть степеней свободы. Во многих случаях колебательное движение атомов не возбуждается. Но если колебания совершаются и их амплитуды малы (по сравнению с расстоянием между атомами), то такие колебания можно считать гармоническими. Атомы в этом случае являются гармоническими осцилляторами. Но осциллятор обладает как кинетической, так и потенциальной энергией. Для гармонического осциллятора, как известно из механики, средние значения кинетической и потенциальной энергии равны между собой. Тогда по закону равнораспределения на каждую колебательную степень свободы приходится kT/2 в виде кинетической энергии и kT/2 в виде потенциальной энергии. Энергия, приходящаяся на одну колебательную степень свободы равна не kT/2, а 2. kT/2= kT. Поэтому при подсчете степеней свободы надо число колебательных степеней свободы удвоить.
Для двухатомного газа
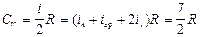 ,
,
 |
причем СV не зависит от температуры. Экспериментально было доказано (рис.8.3.), что в определенном интервале температур эта теплоемкость составляет всего (5/2)R, при очень низких температурах она уменьшалась до (3/2)R, а при высоких становится больше 3R.
Это означает, что при низких температурах молекулы участвуют только в поступательном движении. По мере повышения температуры Т молекулы начинают совершать и вращательные движения. И лишь при высоких температурах она совершает все три вида движения (добавляется колебательное).
Классическая теория такое поведение объяснить не может. Объяснение было получено в рамках квантовой теории. В зависимости теплоемкости от температуры проявляются квантовомеханические свойства молекул - энергия вращательного и колебательного движения у них меняется скачками на величину hn, где n- частота вращения или колебания, h - постоянная Планка. Так как получить такой прирост энергии молекула может лишь при соударении с другой, движущейся с большей поступательной скоростью, то при низких температурах колебания и вращения не происходят (соответствующие степени свободы «вымораживаются»). При более высокой температуре средняя энергия, приходящаяся на каждую из этих степеней, зависит от соотношения между hn и kT.
Дата добавления: 2015-04-19; просмотров: 2443;
