Внутреннее трение (вязкость газов). Теплопроводность газов.

Вязкость газов (это же касается и жидкостей) – это свойство, благодаря которому выравниваются скорости движения разных слоев газа (жидкости). Из-за вязкости сила ветра уменьшается с течением времени, успокаиваются морские волны. Выравнивание скоростей соседних слоев газа (если они разные) происходит потому, что из слоя газа с большей скоростью переносится импульс к слою газа с меньшей скоростью. Так как этот процесс связан с переносом импульса, то газ ведет себя так, как если бы на него действовала некоторая сила – сила внутреннего трения.

Ньютон установил, что при небольших скоростях (ламинарное течение) сила внутреннего трения, действующая между слоями газа (жидкости), площадью dS определяется выражением:

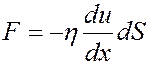(1)

где η – коэффициент динамической вязкости, du/dx – градиент скорости в направлении оси x.

Коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади слоя (между слоями единичной площади) при единичном градиенте скорости.

Если слои газа движутся направленно с некоторой скоростью, то на хаотическое, тепловое движение молекул со скоростью накладывается направленное движение газа. Поэтому импульс каждой молекулы можно разложить на две составляющих, одна из которых обусловлена хаотическим тепловым, а вторая направленным движением молекул.

Если T = const, то составляющая импульса, обусловленная хаотическим, тепловым движением не изменяется от слоя к слою. Молекулы, которые попадают из слоя с большей скоростью направленного движения в слой с меньшей скоростью, имеют большую составляющую импульса, обусловленную направленным движением. При соударениях эти молекулы передают часть своего импульса молекулам более медленного слоя, которые увеличивают при этом скорость своего направленного движения. И наоборот молекулы более медленного слоя, попадая в более быстрый слой, при соударениях тормозят направленное движение молекул этого слоя.

Таким образом, внутреннее трение в газах обусловлено переносом импульса от слоя к слою в направлении нормали к скорости направленного движения слоев.

Пусть слои газа двигаются параллельно оси Z (рис.1.).

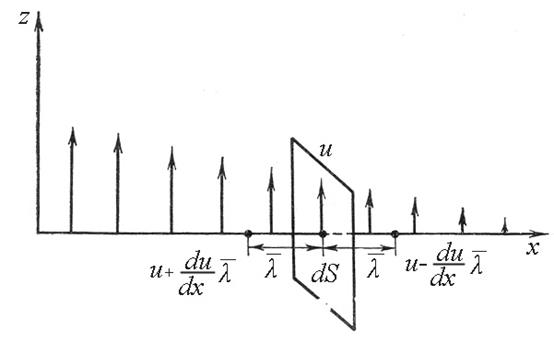
Рис.1.Перенос импульса в газах.

Градиент скорости вдоль оси x равен du/dx. Выберем площадку dS в слое со скоростью u. На расстояниях 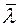от нее слева и справа скорости слоев газа будут соответственно равны:

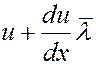
и

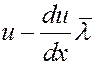
Все направления движений молекул равновероятны из-за полной их хаотичности. Поэтому в направлении оси x движется 1/3 часть всех молекул: из них 1/6 движется слева направо и 1/6 справа налево. За время dt через площадку dS слева направо пройдет

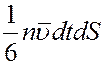
молекул, которые перенесут через эту площадку импульс:

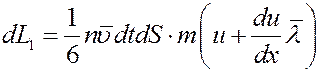(2)

Одновременно за это же время такое же количество молекул пройдет через площадку dS справа налево, при этом они перенесут импульс:

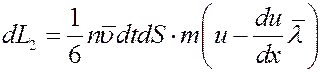(3)

За это же время из площадки dS слоя, скорость которого равна u, вылетит такое же количество молекул и вправо и влево. Но так как скорости этих молекул одинаковые, равные u и направлены в разные стороны изменение импульса слоя при этом будет равно нулю. С учетом этого импульс, который перенесется через площадку dS в положительном направлении оси x, равен:

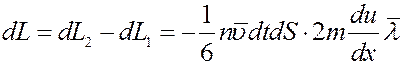(4)

Учитывая, что mn = ρ – плотность газа, из (4) получим:

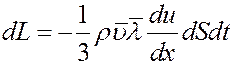(5)

Из (5) видно, что знак минус показывает, что импульс переносится в направлении уменьшения скорости слоев.

Согласно II закону Ньютона изменение импульса в единицу времени равно действующей силе:

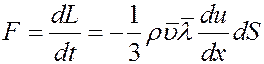(6)

Сравнивая (6) и (1) найдем коэффициент динамической вязкости:

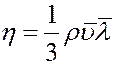(7)

В системе CI:

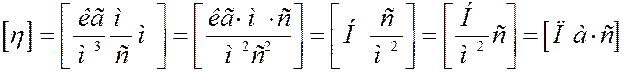
Известно, что ρ ~ p, а 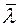~ 1/p. Следовательно, из (7) вытекает, что η не зависит от давления газа. Этот факт объясняется следующим образом. С уменьшением давления уменьшается концентрация молекул, а значит и их число, участвующее в переносе. Однако 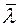при этом увеличивается. Поэтому импульс, который переносит одна молекула, так же увеличивается. В результате суммарный импульс, переносимый молекулами при данном градиенте скорости не изменяется.

Из (7) видно, что η увеличивается с ростом температуры:

.

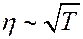На самом деле η растет несколько быстрее чем 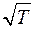, потому что с ростом температуры не только увеличивается скорость молекулы, но и уменьшается эффективный диаметр молекул (формула Сезерленда), что приводит к увеличению .

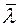Теплопроводность. Если газ неравномерно нагрет, т.е. температура одной его части больше другой, то наблюдается выравнивание температуры: более нагретая часть газа охлаждается, а более холодная нагревается. Очевидно, что выравнивание температуры связано с потоком тепла от нагретой части газа к холодной.

Явление возникновения потока тепла в газе (или в любом другом веществе) называется теплопроводностью. В любом теле, в частности в газе, предоставленном самому себе, теплопроводность приводит к выравниванию температур.

Фурье установил опытами, что количество теплоты, которое передается через площадку dS за время dt в направлении нормали к площадке пропорционально градиенту температуры.

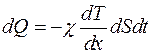(8)

где χ – коэффициент теплопроводности. Он зависит от рода газа и условий, при которых газ находится.

В системе CI:

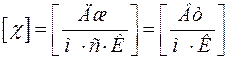
Физический смысл χ: Коэффициент теплопроводности численно равен количеству теплоты, которое переносится через единичную площадку, в единицу времени при единичном градиенте температуры.

Знак «-» в правой части (8) показывает, что направление, в котором возрастает температура и направление, в котором переносится тепло противоположные, т.е. теплота переносится в направлении уменьшения температуры.

Рассмотрим площадку dS перпендикулярную оси x, вдоль которой поддерживается постоянная разность температур. Температура слева от площадки больше чем справа T₁ > T₂ (рис.2).

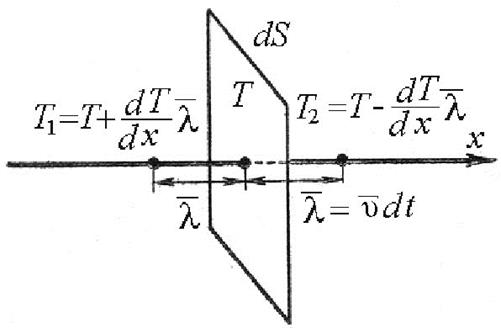
Рис.2. Теплопроводность газов.

Через площадку dS проходят молекулы как слева направо, так и справа налево и если давление газа везде одинаково, то число молекул, которые проходят через площадку слева и справа за время dt очевидно одинаково. Однако молекулы, которые проходят слева движутся из области с более высокой температурой, чем те, которые проходят через площадку справа.

Поэтому возникает поток теплоты, равный разности энергий переносимых молекулами слева и справа. Последние столкновения перед площадкой dS слева и справа, будут происходить на расстояниях 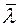, где температура слоев газа равна соответственно:

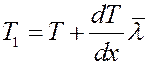
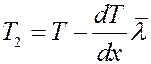
В направлении оси x двигается 1/3 всех молекул: 1/6 слева направо и 1/6 справа налево. Средняя кинетическая энергия молекул газа равна:

.

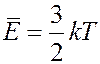За время dt через площадку dS слева направо пройдет

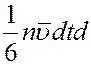
молекул, каждая из которых обладает кинетической энергией

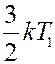
Они перенесут через площадку dS энергию:

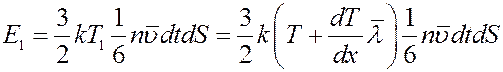(9)

Одновременно за это же время через площадку пройдет такое же количество молекул справа налево, каждая из которых обладает энергией:

.

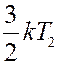Они перенесут через площадку энергию:

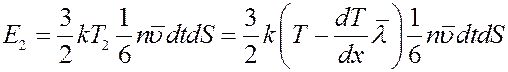(10)

С учетом этого количество теплоты (энергия), которая переносится молекулами через площадку dS, будет равна разности кинетических энергий молекул проходящих через площадку.

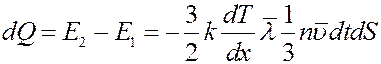(11)

Умножим и разделим правую часть (11) на массу молекулы m и число Авогадро N_A:

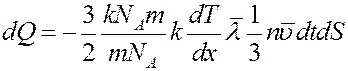(12)

Учтем, что: mn = ρ – плотность газа, а величина

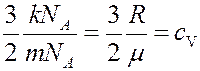
где mN_A = μ – молярная масса, c_V – удельная теплоемкость газа при постоянном объеме. С учетом этого из (12) получим:

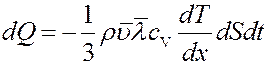(13)

Сравнивая (13) и (8) определим коэффициент теплопроводности:

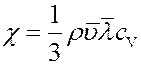(14)

Из (14) следует, что χ не зависит от давления p по той же причине, что и η (ρ ~ p, а λ ~ 1/p). Коэффициент теплопроводности зависит от T, так же как и η:

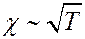
Однако для многоатомных газов необходимо учитывать некоторое возрастание теплоемкости c_V с увеличением температуры.

При определении коэффициентов переноса (D, η, χ) считалось, что молекулы двигаются через площадку в направлении нормали к ней. Однако это не так. Более строгие расчеты показывают, что через площадку двигается 1/4 часть всех молекул. С учетом этого:

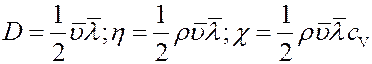
Сравнивая выражения для коэффициентов переноса, получим связь между ними:

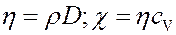
Любой из коэффициентов переноса, определенный экспериментально, позволяет найти среднюю длину свободного пробега молекул, следовательно, позволяет определить размеры (эффективный диаметр) молекул. Величины значений сечений молекул данного газа, определенные из различных коэффициентов переноса, совпадают и называются газокинетическими сечениями.