Внутренняя энергия реального газа. Эффект Джоуля-Томсона. Сжижение газов. Получение низких температур.

Известно, что внутренняя энергия идеального газа определяется кинетической энергией хаотического движения молекул. В случае реального газа необходимо учитывать потенциальную энергию взаимодействия молекул, которая определяется межмолекулярными Ван-дер-Ваальсовскими силами. Следовательно, внутренняя энергия реального газа определяется следующим уравнением:

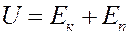(1)

Кинетическая энергия молекул пропорциональна температуре. Для одного моля газа:

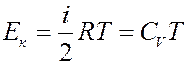(2)

где C_V – молярная теплоемкость при постоянном объеме.

Потенциальная энергия молекул зависит от расстояния между ними, поэтому она должна быть функцией объема газа. Следовательно, согласно (1), внутренняя энергия реального газа должна быть функцией двух параметров состояния: T и V.

Определим потенциальную энергию реального газа.

При расширении газа выполняется работа за счет изменения внутреннего молекулярного давления:

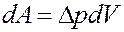(3)

где ∆p = a/V² – внутреннее молекулярное давление. Эта работа равна изменению потенциальной энергии:

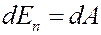(4)

Проинтегрировав (4) с учетом (3) получим потенциальную энергию реального газа:

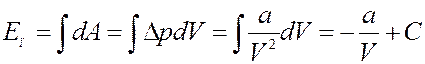(5)

Значение постоянной C необходимо выбрать таким образом, чтобы потенциальная энергия газа при V→∞ стремилась к нулю, потому что если V→∞, то реальные газы по своим свойствам приближаются к идеальным газам:

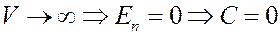
Тогда из (5) потенциальная энергия реального газа:

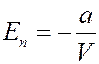(6)

С учетом (6) и (2) из (1) получим внутреннюю энергию реального газа:

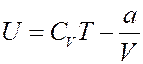(7)

Если газ расширяется адиабатически без выполнения работы (расширение газа в пустоту), то согласно I началу термодинамики его внутренняя энергия должна оставаться постоянной:

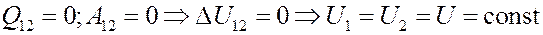
Отсюда следует, что для идеального газа:

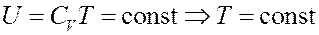
То есть температура идеального газа при расширении в пустоту не изменяется.

Для реального газа:

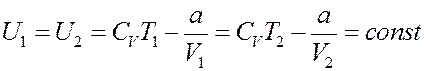
Или:

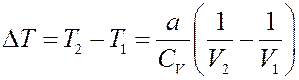(8)

Из (8) видно, что при расширении V₂ > V₁, тогда ∆T < 0, т.е. температура реального газа при расширении в пустоту уменьшается. Однако, при некоторых условиях, при расширении температура газа может и увеличиваться.

Впервые явление изменения температуры при расширении газа было исследовано Джоулем и Томсоном (рис.1).

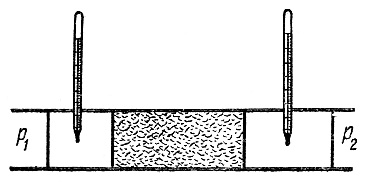
Рис.1. Схема опыта Джоуля-Томсона

Сосуды с газом соединены теплоизолированной трубкой. В трубке находится пористая перегородка (керамика, вата и т.д.). По обе стороны от перегородки установлены термометры. Пусть p₁ > p₂. Процесс расширения газа адиабатный (трубка теплоизолирована). Гидродинамическое сопротивление перегородки приводит к тому, что газ выходит из перегородки при более низком давлении, чем давление при входе. При этом газ расширяется, или, как говорят, дросселируется.

Дросселем называется любое приспособление, которое создает сопротивление протеканию газа (например, вместо керамики узкое отверстие).

Чтобы течение газа через перегородку было стационарным, используется компрессор, поддерживающий разность давлений постоянной.

Явление изменения температуры газа при его адиабатном расширении дросселированием называется эффектом Джоуля-Томсона. Опытным путем установлено, что для большинства газов при комнатных температурах ∆T < 0 – газы при расширении охлаждаются. Однако для некоторых газов (водород, гелий) ∆T > 0 – газы при расширении нагреваются.

Охлаждение газа при расширении называется положительным, а нагревание отрицательным эффектом Джоуля-Томсона.

Определим условия, от которых зависит знак эффекта (рис.2).

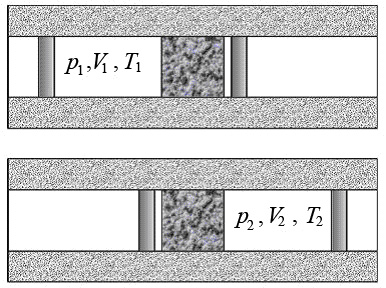
Рис.2. Расширение газа при прохождении пористой перегородки

Выделим слева от перегородки некоторый объем газа V₁. После прохождения газом перегородки его объем станет V₂. Газ расширяется адиабатно, поэтому согласно I началу термодинамики изменение внутренней энергии газа равно работе, выполненной им:

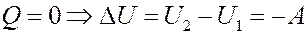(9)

Определим величину работы. Слева работу над выделенным объемом газа выполняет остальной газ из первого сосуда:

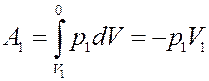(10)

Знак « - » показывает, что работа выполняется над газом. Справа, газ, расширяясь, сам, выполняет работу над остальным газом во втором сосуде:

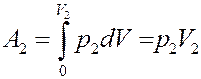(11)

Работа, выполненная газом:

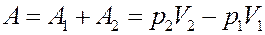(12)

С учетом (12) найдем изменение внутренней энергии газа из (9):

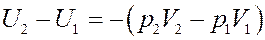
Раскрыв скобки получим:

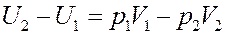(13)

Или:

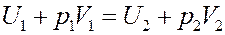(14)

Известно, что U + pV = I – энтальпия. Из (14) видно, что эффект Джоуля-Томсона протекает при постоянной энтальпии.

Для идеального газа и внутренняя энергия и произведение pV зависят только от температуры. Поэтому и энтальпия I зависит только от температуры. Из равенства энтальпий по обе стороны от перегородки вытекает и равенство температур по обе стороны перегородки для идеального газа. Поэтому для идеального газа эффект Джоуля-Томсона равен нулю ∆T = 0.

У реальных газов внутренняя энергия зависит не только от температуры, но и от объема (7). Поэтому равенство энтальпий (14) еще не свидетельствует о равенстве температур по обе стороны перегородки.

Для газов, которые подчиняются уравнению Ван-дер-Ваальса, знак эффекта Джоуля-Томсона должен зависеть от того, какая из постоянных a или b играет в уравнении большую роль.

Рассмотрим два граничных случая:

1). Пусть молекулы обладают собственным объемом, но не взаимодействуют между собой a = 0. Тогда:

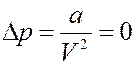
С учетом этого уравнение Ван-дер-Ваальса для одного моля газа принимает вид:

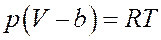
Или:

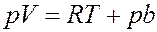(15)

Подставим (15) в (13):

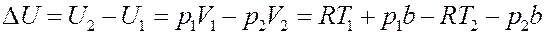
Или:

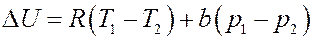(16)

С другой стороны с учетом (7):

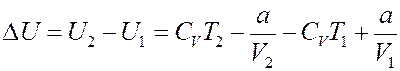
Но a = 0, тогда:

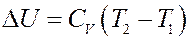(17)

Приравнивая (16) и (17) получим:

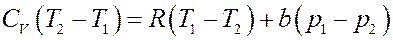
Преобразуем последнее равенство:

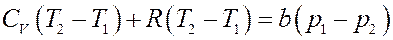
Или:

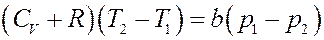
Окончательно:

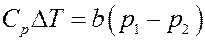(18)

Из (18) следует, что при расширении p₁ > p₂, тогда ∆T > 0 и T₂ > T₁. Следовательно, если собственный объем молекул играет большую роль, чем их взаимодействие (силы отталкивания больше сил притяжения), то температура газа после расширения повышается – эффект отрицательный.

2). Пусть на собственный объем молекул можно не обращать внимания, но их взаимодействие (притяжение) не равно нулю. Тогда в уравнении Ван-дер-Ваальса b = 0 и для одного моля газа оно принимает следующий вид:

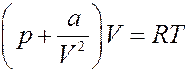
Преобразуем последнее уравнение (раскроем скобки):

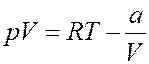(19)

Подставим (19) в (13):

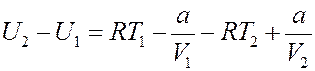(20)

Из (7) следует:

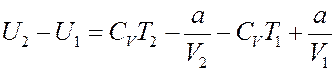(21)

Приравняем (20) и (21):

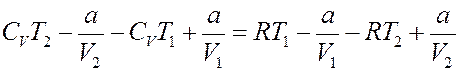
Перегруппируем члены:

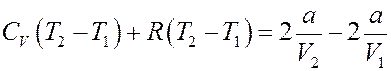
Или:

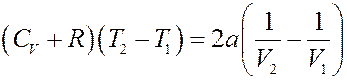
Окончательно получим:

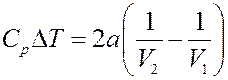(22)

Из (22) следует, что при расширении V₂ > V₁, поэтому ∆T < 0 и T₂ < T₁ – газ при расширении охлаждается. Следовательно, если взаимодействие молекул играет большую роль, чем их собственный объем (силы притяжения больше сил отталкивания) то газ при расширении охлаждается – эффект положительный.

Рассмотрим общий случай, когда надо учитывать как взаимодействие молекул, так и их собственный объем.

Пусть после расширения 1 моля газа его объем V₂ очень большой, поэтому его можно считать идеальным. Тогда согласно уравнению Клапейрона-Менделеева и уравнению (2):

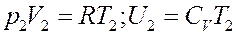(23)

Определим левую часть уравнения (14). Согласно (7):

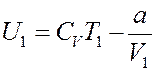(24)

Запишем уравнение Ван-дер-Ваальса для одного моля газа:

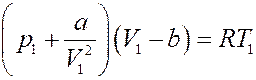
Преобразуем его:

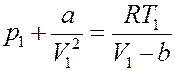
Или:

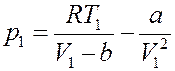
Умножим левую и правую часть последнего равенства на V₁:

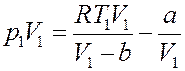(25)

Преобразуем первое слагаемое справа в (25):

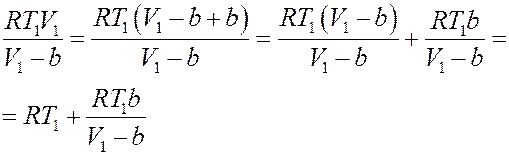(26)

Подставим (26) в (25):

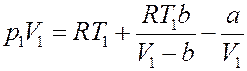(27)

Подставим (23), (24) и (27) в (14):

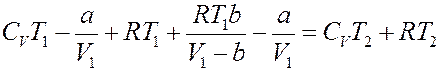
Или:

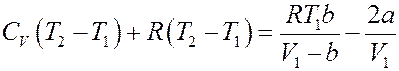
Или:

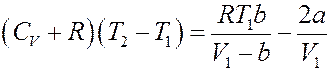
Окончательно получим:

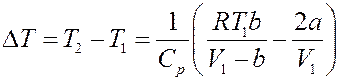(28)

Знак ∆T определяется знаком выражения в скобках. Нулевой эффект (∆T = 0) будет наблюдаться, если:

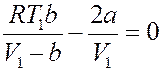
Или:

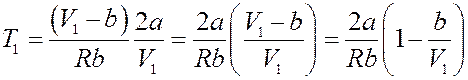
Этому уравнению соответствует кривая T₁ = f(V₁), точки которой определяют значение параметров T₁ и V₁ (начальных параметров), при которых ∆T = 0 (рис.3).

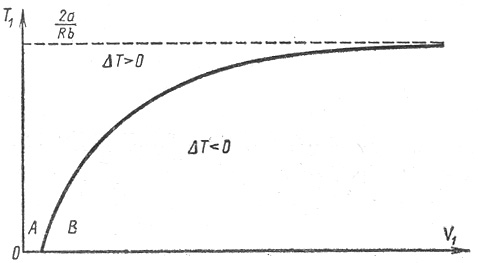
Рис.3. Области эффекта Джоуля-Томсона

Точки, которые лежат выше кривой, определяют значения T₁ и V₁, при которых ∆T > 0 и эффект отрицательный. Точки, лежащие ниже кривой определяют значения начальных параметров, при которых ∆T < 0 и эффект положительный. При больших значениях V₁, (V₁ → ∞), кривая асимптотически стремится к значению:

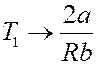
Это наибольшее значение температуры, при которой возможно изменение знака эффекта – называется температурой инверсии. Выше этой температуры эффект всегда отрицательный. Точки самой кривой соответствуют температуре, при переходе через которую, знак эффекта изменяется. Эта кривая называется кривой инверсии.

Из графика видно, что если расширение газа происходит при малых начальных объемах (V₁), то эффект будет отрицательным даже при низких начальных температурах – область А. Увеличение начального объема – область В изменяет знак эффекта и газ будет охлаждаться при расширении.

Температуры инверсии некоторых газов: H₂ – 192,7 K, O₂ – 1063 K, He – 40 K.

Эффект Джоуля-Томсона используется в технике для сжижения газов.

Для того чтобы перевести газ в жидкое состояние, его необходимо охладить до температуры ниже критической. Это можно сделать разными способами.

Метод Линде: 1895 год (рис.4).

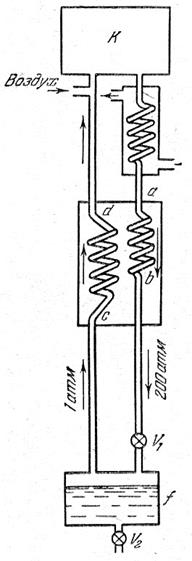
Рис.4. Схема машины Линде

Сжатый компрессором K газ проходит через змеевик, охлаждаемый проточной водой, где отдает тепло, выделившееся при сжатии. Затем газ проходит через змеевик ab теплообменника к дроссельному вентилю V₁. При дросселировании газ резко расширяется и при этом охлаждается (эффект Джоуля-Томсона).

После первого расширения температура газа понижается недостаточно для сжижения, и, поэтому газ возвращают обратно в компрессор через змеевик cd теплообменника, где он охлаждает перед дросселированием идущую навстречу порцию газа. Теплообменник представляет собой две трубки, вставленные одна в другую и изогнутые в виде змеевика. По внутренней трубке газ идет к дросселю, по внешней трубке навстречу движется охлажденный после дросселирования газ.

В процессе работы установки температура газа постоянно уменьшается и становится ниже критичной. Газ конденсируется и собирается в приемнике f. Та часть газа, которая не сконденсировалась, возвращается в компрессор и т.д. Этот способ сжижения газа требует много энергии.

Позднее были разработаны другие, более экономичные способы сжижения газов. В машине Клода (1902 год) (рис.5) используется как способ охлаждения газа при дросселировании, так и способ охлаждения газа при адиабатном его расширении с выполнением работы.

Приспособление, в котором газ, расширяясь, выполняет работу и за счет этого охлаждается, называется детандером. Простейший детандер – цилиндр с поршнем. Капица в качестве детандера применил турбину, которая приводилась во вращение газом, сжатым компрессором – турбодетандер. Работу, которую выполняет сжатый газ в детандере, используют для облегчения работы компрессора.

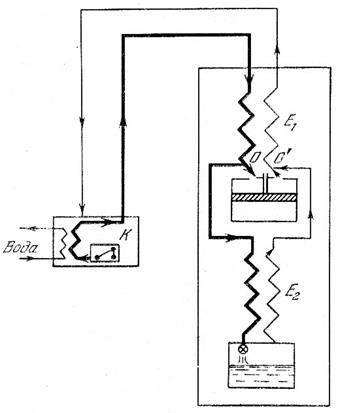
Рис.5. Схема машины Клода

Газ, сжатый компрессором, охлаждается проточной водой и проходит через теплообменник E₁, где он разделяется на два потока. Первый поток проходит через дроссель и охлаждается благодаря эффекту Джоуля-Томсона. Второй поток (~ 80% всего газа) поступает в детандер, расширяется в нем, совершая работу, и за счет этого охлаждается.

После детандера охлажденный газ возвращается в теплообменник E₁, где охлаждает встречную порцию газа, сжатого компрессором. К этому потоку газа в точке O′ присоединяется газ, охлажденный в результате дросселирования. До этого, проходя через теплообменник E₂, он также охлаждал встречный газовый поток.

Из схемы машины Клода видно, что газ, охлажденный в детандере, используется для предварительного охлаждения газа перед дросселированием. Турбодетандеры при небольших размерах обладают большой производительностью. КПД ~ 17%, на получение 1кг жидкого газа уходит ~ 1,1 кВт/час энергии.

Понятие низкой температуры относительное. Оно определяется областью явлений, которые рассматриваются при разных температурах. Для получения низких температур используют следующие методы: испарение жидких газов; эффект Джоуля-Томсона; адиабатичное расширение газа с выполнением работы.

Температура кипения жидкого газа зависит от давления пара над ним. Поэтому если понизить давление пара, откачивая его, то температуру кипения жидкого гелия можно понизить ~ 0,7K.

Для получения сверхнизких температур используют метод адиабатного размагничивания парамагнитных солей. Он основан на зависимости энтропии парамагнитной соли от напряженности магнитного поля.

Атомы парамагнитного вещества обладают магнитными моментами. В обычных условиях эти магнитные моменты ориентированы беспорядочно из-за теплового движения, в котором участвуют молекулы соли (рис.6,а):

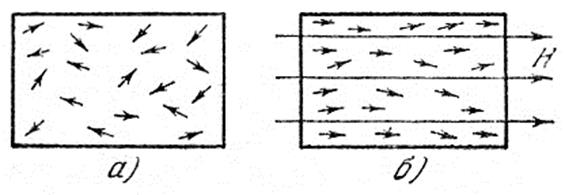
Рис.6. Ориентация магнитных моментов молекул парамагнитной соли

Если такую соль поместить в сильное магнитное поле, то магнитные моменты будут ориентироваться вдоль поля (рис.6,б). Этот процесс называется намагничиванием. Следовательно, магнитное поле приводит к тому, что степень беспорядка (магнитного) уменьшается. Поэтому уменьшается и связанная с ним энтропия.

Парамагнитную соль охлаждают жидким гелием до ~ 1K и намагничивают. После этого намагниченную, охлажденную соль изолируют от жидкого гелия и адиабатно размагничивают, удаляя из магнитного поля.

При адиабатическом процессе:

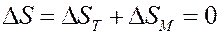
где ∆S_T – изменение энтропии, обусловленное тепловым движением молекул (температурой), ∆S_M – изменение энтропии, обусловленное магнитными свойствами.

При адиабатном размагничивании ∆S_M > 0 – энтропия, обусловленная магнитными свойствами, возрастает, потому что магнитные моменты молекул в отсутствие магнитного поля ориентируются беспорядочно (рис.6,а). Следовательно, при этом должна уменьшиться энтропия, связанная с тепловым движением (температурой) ∆S_T < 0. Поэтому температура парамагнитной соли уменьшится. Используя этот метод можно получить температуры ~ 10^-5K.

При низких температурах резко изменяются физические свойства вещества (сверхпроводимость, сверхтекучесть и т.д.).