Теплопроводность газов.
Выравнивание температуры за счет переноса молекулами энергии между частями вещества, которые первоначально имели различную температуру, называется теплопроводностью. Причина этого явления в том, что хаотическое тепловое движение молекул газа, имеющих различные скорости, а, следовательно, и различные средние кинетические энергии, приводит к направленному переносу энергии в форме теплоты. Количество теплоты, переносимое через элементарную площадку в направлении нормали к этой площадке, выражается законом Фурье:
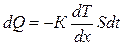 , (7.4.1)
, (7.4.1)
где Т – абсолютная температура, 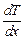 – градиент температуры (вектор, направленный в сторону убывания температуры), К - коэффициент теплопроводности, численно равный количеству теплоты, переносимому в единицу времени через единичную площадку при единичном градиенте температуры.
– градиент температуры (вектор, направленный в сторону убывания температуры), К - коэффициент теплопроводности, численно равный количеству теплоты, переносимому в единицу времени через единичную площадку при единичном градиенте температуры.
Коэффициент теплопроводности связан с некоторыми молекулярными характеристиками по формуле:
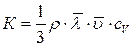 ([к]=Вт/м·К) (7.4.2)
([к]=Вт/м·К) (7.4.2)
Связь коэффициентов вязкости, теплопроводности и диффузии:
h =r·D,
К=cV ·h= cV·r ·D
Так как h  , cV~1/m0 , то К ~
, cV~1/m0 , то К ~ 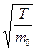 . Коэффициент теплопроводности К не зависит от давления. Такое состояние сохраняется до тех пор, пока средняя длина свободного пробега молекул не станет равной размерам сосуда. При дальнейшем понижении давления плотность газа будет уменьшаться, но длина свободного пробега молекул не будет изменяться, так как не сможет стать больше размеров сосуда. В этом случае вязкость и теплопроводность изменяются пропорционально давлению.
. Коэффициент теплопроводности К не зависит от давления. Такое состояние сохраняется до тех пор, пока средняя длина свободного пробега молекул не станет равной размерам сосуда. При дальнейшем понижении давления плотность газа будет уменьшаться, но длина свободного пробега молекул не будет изменяться, так как не сможет стать больше размеров сосуда. В этом случае вязкость и теплопроводность изменяются пропорционально давлению.
Связь теплопроводности газов с давлением при малых давлениях используют при создании специальных сосудов для хранения холодных и горячих тел. Теплопроводность уменьшается благодаря вакууму, который поддерживается в двойной снетке (термосы, или сосуды Дьюара).
Глава 8. Основы термодинамики
Дата добавления: 2015-04-19; просмотров: 1085;
