Стаціонарні та критичні точки.
Точки, що належать області визначення функції, в яких перша похідна перетворюється в нуль або зазнає розриву, називаються критичними точками І роду (або стаціонарними).
Якщо при переході через критичну точку 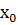 похідна
похідна 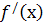 змінює знак з мінуса на плюс, то функція
змінює знак з мінуса на плюс, то функція 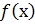 має в точці
має в точці 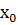 мінімум, і максимум, коли похідна змінює знак з плюса на мінус. Якщо ж при переході через критичну точку
мінімум, і максимум, коли похідна змінює знак з плюса на мінус. Якщо ж при переході через критичну точку 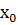 похідна
похідна 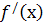 не змінює знака, то функція
не змінює знака, то функція 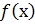 в точці
в точці 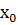 не має екстремуму.
не має екстремуму.
Правило знаходження екстремумів функції 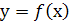 за допомогою першої похідної.
за допомогою першої похідної.
1. Знайти похідну 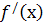 .
.
2. Знайти критичні точки І роду.
3. Дослідити знак похідної в проміжках, на які знайдені критичні точки ділять область визначення функції 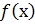 . Критична точка
. Критична точка 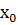 є точкою мінімуму, якщо похідна змінює знак з мінуса на плюс, і точкою максимума , якщо змінює знак з плюса на мінус. Якщо знак похідної не змінюється, то в точці
є точкою мінімуму, якщо похідна змінює знак з мінуса на плюс, і точкою максимума , якщо змінює знак з плюса на мінус. Якщо знак похідної не змінюється, то в точці 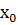 функція екстремуму не має.
функція екстремуму не має.
4. Обчислити значення функції в точках екстремуму.
Приклад 2. Дослідити на екстремум функцію 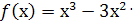
Розв’язання.
Знаходимо похідну функції 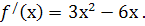 Знаходимо критичні точки
Знаходимо критичні точки
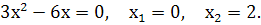
Критичні точки ділять область визначення функції на проміжки, в кожному із яких знаходимо знак похідної
| х |
| + |
| - |
| + |
| max |
| min |
Знаходимо значення функції в точках екстремуму :
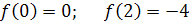
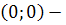 max;
max; 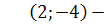 min.
min.
Дата добавления: 2015-06-27; просмотров: 6541;
