Точки перегину графіка функції.

Точка графіка функції 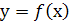, яка поділяє проміжки опуклості протилежних напрямів цього графіка, називається точкою перегину.

Точками перегину можуть бути тільки критичні точки ІІ роду, тобто точки, які належать до області визначення функції 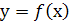, в яких друга похідна 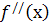перетворюється в нуль, або зазнає розриву.

Якщо при переході через критичну точку 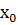друга похідна 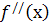змінює знак, то графік функції має точку перегину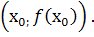

Правило знаходження точок перегину графіка функції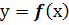

1. Знайти другу похідну .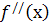

2. Знайти критичні точки ІІ роду, тобто точки, в яких 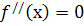, або зазнає розриву.

3. Дослідити знак другої похідної 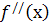в проміжках, на які знайдені критичні точки ділять область визначення функції 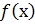. Якщо друга похідна змінює знак, то 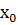є точкою перегину, якщо ж знаки однакові, то точки перегину немає.

4. Обчислити значення функції в точках перегину.

Приклад 2. Знайти точки перегину кривої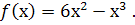

Розв’язання.

Знаходимо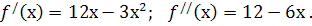

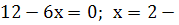критична точка.

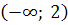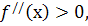В проміжку маємо а в проміжку 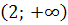маємо 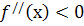, то при 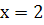крива має точку перегину.

Знайдемо ординату цієї точки :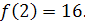

Отже, 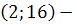точка перегину.