Фазовые методы исследования нелинейных систем

Наличие нелинейных элементов в системе приводит к необходимости описания поведения таких систем, с помощью дифференциальных уравнений высоких порядков. Очень часто решений таких уравнений в конечном виде не существует, поэтому для описания поведения нелинейных систем широко используют приближенные графоаналитические методы, один из которых является фазовый метод.

Сущность фазового метода: состояние нелинейной системы, в любой момент времени представленная в виде некоторой изображающей точки М фазового пространства, координатами которых является выходная величина системы и ее производные по времени:

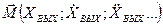
Изменение состояния системы приводит к изменению координат изображающей точки, таким образом при применении состояния системы изображающая точка перемещается в фазовом пр-ве по некоторой траектории – фазовая траектория.

Для исследования систем, используется фазовая плоскость:

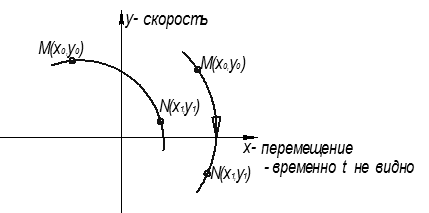
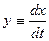
Время в явном виде не отражается на фазовой траектории.

Совокупность фазовых траекторий, характеризующих возможные движения в системе, называется фазовым портретом системы.

Для получения уравнения фазовой траектории используется дифференциальное уравнение системы:

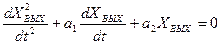(16.1)

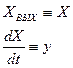
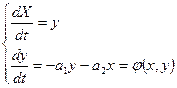
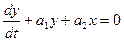
Делим первое выражение на второе:

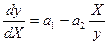– выражение для определения фазовых траекторий (16.2)

Свойства фазового портрета:

· если функция 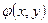непрерывна и дифференцируема, то через любую точку фазовой плоскости можно провести одну единственную фазовую траекторию. Исключение: особые точки, для которых выполняется условие:

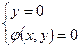– точки равновесия и именно в этих точках фазовые траектории могут пересекаться.

· В верхней фазовой полуплоскости, движение по фазовым траекториям происходит слева на право и, наоборот (в нижней):

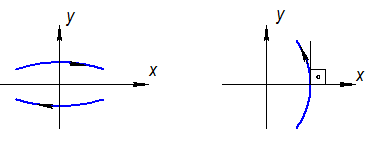
· Фазовые траектории пересекают ось Х под прямым углом, за исключением …… особых точек

· Особые точки, расположенные на оси абсцисс соответствуют состояниям равновесия и остановке движения