Виды особых точек

Существует несколько типовых особых точек. Тип особой точки определяется видом корней характеристического уравнения в виде:

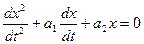(16.3)

Корни характеристического уравнения:

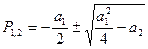
Разновидности корней уравнения:

· Корни чисто мнимые при: а₁ = 0; а₂ > 0

· Корни вещественные. С положительной вещественной частью: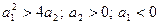

· Корни вещественные отрицательные: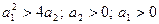

· Комплексные корни с положительной вещественной частью: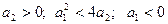

· Комплексные корни с отрицательной вещественной частью: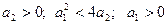

· Корни вещественные разного знака: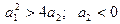

Если корни мнимые:

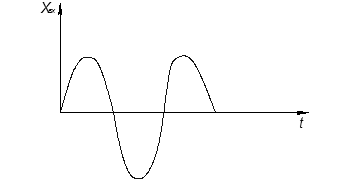
А – характеризуют амплитуду колебаний

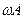– частота колебаний увеличенная в А раз

О – центр

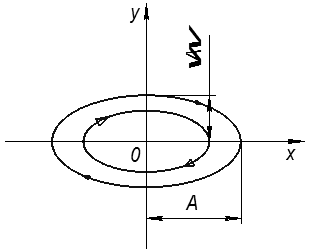
Если корни вещественно положительные:

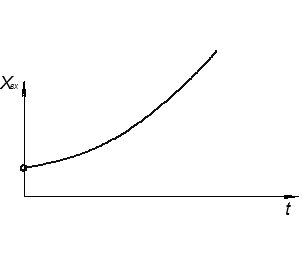
О – неустойчивая точка

Если корни вещественно отрицательные:

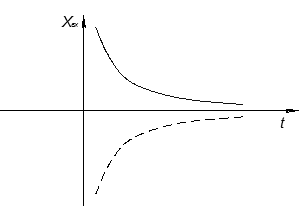
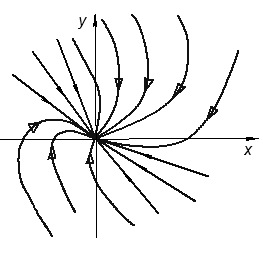
О – устойчивая точка

Если корни с положительной обратной связью:

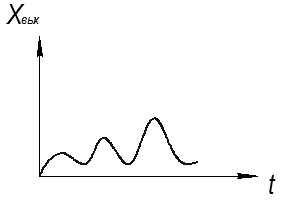
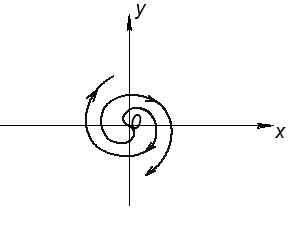
О – неустойчивый фокус

Если корни комплексные с отрицательной обратной связью:

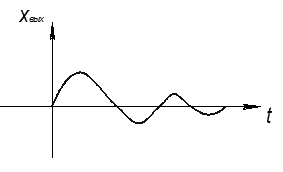
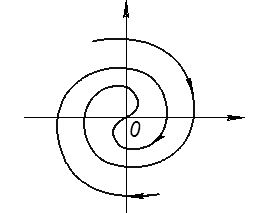
О – устойчивый фокус

Если корни вещественные, но разного знака:

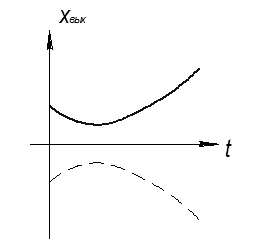
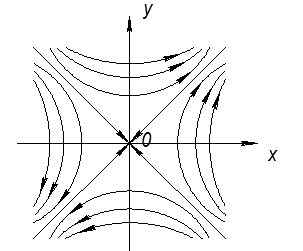
О – седло (всегда неустойчиво)