ВЫЧИСЛЕНИЕ РАЗНОСТИ ШИРОТ И РАЗНОСТИ ДОЛГОТ ДВУХ ТОЧЕК
Задача № 7.1: 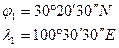
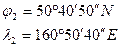
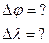
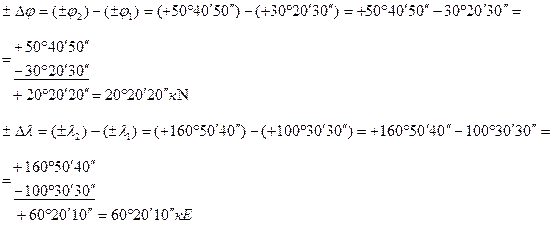
Задача № 7.2: 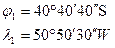
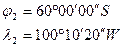
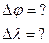
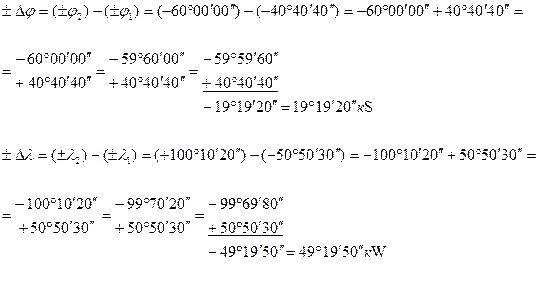
Задача № 7.3: 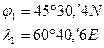
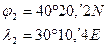
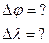
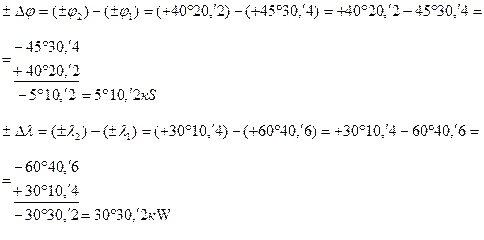
Задача № 7.4: 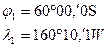
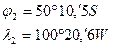
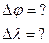

Задача № 7.5: 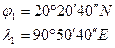
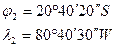
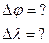
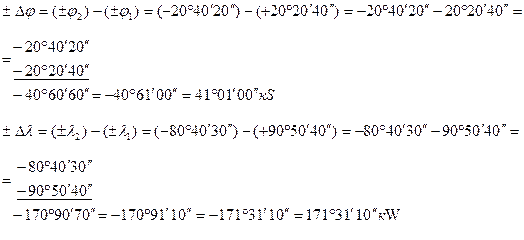
Задача № 7.6: 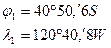
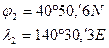
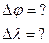
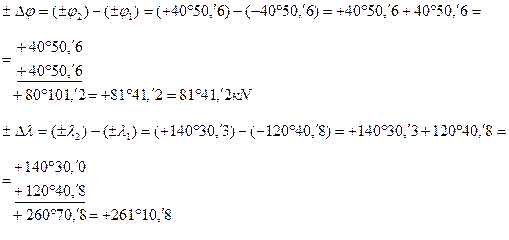
Поскольку 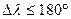 , то величину
, то величину 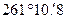 вычитают из трехсот шестидесяти градусов, а знак – меняют на противоположный:
вычитают из трехсот шестидесяти градусов, а знак – меняют на противоположный:
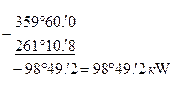
Характерные причины ошибочного вычисления разности широт и разности долгот двух точек (от греч. character – отличительная черта, признак):
1. Неразборчивое написание цифр числового значения широты и долготы точки, в результате чего цифру 3, например, можно прочитать как цифру 9, цифру 5 – как цифру 6 и т.п.
2. Неправильное написание формулы для вычисления  и
и 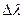 .
.
3. Невнимательность при написании в скобках алгебраической формулы (6.1) или (6.2) числовых значений широты или долготы точки, в результате чего, например, вместо числового значения 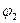 записывают числовое значение
записывают числовое значение 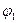 и т.п.
и т.п.
4. Неправильное применение так называемого «правила знаков» во время раскрытия скобок алгебраической формулы.
5. Невнимательность при сложении, вычитании чисел и других арифметических действий (от греч. arithmos – число).
Первые четыре причины приводят к грубой ошибке (к грубой погрешности) вычисления  и
и 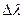 , которую в практике судовождения принято называть промахом.
, которую в практике судовождения принято называть промахом.
Для исключения промаха вычисления  и
и 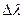 необходимо соблюдать правила штурманской культуры математических вычислений, которая начинается с внешнего вида судоводителя, стиля его работы и порядка на штурманском столе (от лат. cultura – возделывание, воспитание, образование, развитие, почитание):
необходимо соблюдать правила штурманской культуры математических вычислений, которая начинается с внешнего вида судоводителя, стиля его работы и порядка на штурманском столе (от лат. cultura – возделывание, воспитание, образование, развитие, почитание):
1. Внешний вид судоводителя должен быть опрятным.
2. Вычисление навигационных величин должно производиться быстро, но без спешки и нервозности.
3. На штурманском столе не должно быть ничего лишнего, мешающего работе судоводителя.
4. Написание цифр и символов формулы (от греч. symbolon – знак, опознавательная примета) должно быть разборчивым и аккуратным, чтобы исключить неоднозначное прочтение этих цифр и символов.
5. Формулы для вычисления  и
и 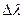 необходимо выводить с помощью специального чертежа.
необходимо выводить с помощью специального чертежа.
6. Вычисление  и
и 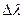 с помощью алгебраических формул (6.1) и (6.2) должно производиться в следующей последовательности:
с помощью алгебраических формул (6.1) и (6.2) должно производиться в следующей последовательности:
6.1 Записывают алгебраическую формулу (6.1) для вычисления  и алгебраическую формулу (6.2) для вычисления
и алгебраическую формулу (6.2) для вычисления 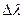 .
.
6.2 В скобках алгебраической формулы (6.1) записывают числовые значения 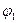 и
и 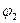 со своими знаками «плюс» или «минус», а в скобках формулы (6.2) записывают числовые значения
со своими знаками «плюс» или «минус», а в скобках формулы (6.2) записывают числовые значения 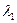 и
и 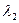 со своими знаками.
со своими знаками.
6.3 Раскрывают скобки алгебраической формулы с соблюдением так называемого «правила знаков»: «плюс» на «минус» дает «минус», а «плюс» на «плюс» и «минус» на «минус» дают «плюс».
6.4 Производят сложение или вычитание числовых величин 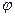 и
и 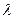 с соблюдением определенной последовательности этих действий с градусами, минутами и секундами угловых величин.
с соблюдением определенной последовательности этих действий с градусами, минутами и секундами угловых величин.
6.5 Проверяют правильность вычисления  и
и 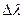 с помощью так называемого «проверочного чертежа».
с помощью так называемого «проверочного чертежа».
 Специальный чертеж для вывода формул по вычислению
Специальный чертеж для вывода формул по вычислению  и
и 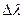 вычерчивают от руки (без применения чертежных инструментов) в тетради для черновых записей.
вычерчивают от руки (без применения чертежных инструментов) в тетради для черновых записей.
Порядок построения специального чертежа для вывода формулы по вычислению  (рисунок 7.1):
(рисунок 7.1):
1. Вычерчивают окружность EPNQPS, которая является истинным меридианом на земном шаре.
2. Через центр окружности О проводят вертикальную линию PNPS, которая является осью вращения Земли.
3. Через центр окружности О проводят горизонтальную линию EQ, которая является линией пересечения плоскости земного экватора с плоскостью истинного меридиана EPNQPS.
4. Под углом примерно 30º к линии ОQ проводят радиус окружности ОА, который является нормалью точки А к поверхности земного шара. Поэтому угол АОQ между плоскостью земного экватора и нормалью точки А к поверхности земного шара обозначают дугой со стрелкой и подписывают 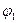 .
.
5. Под углом примерно 60º к линии ЕQ проводят радиус окружности ОВ. Угол ВОQ обозначают дугой со стрелкой и подписывают 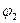 .
.
6. Дугу меридиана АВ обозначают стрелкой, которая показывает направление движения судна из начальной точки А в конечную точку В в сторону северного истинного полюса земли PN. Поэтому дугу АВ подписывают  .
.
Таким образом, на рисунке 7.1 изображено меридиональное сечение земного шара. Судно движется вдоль линии истинного меридиана северного полушария из начальной точки А в конечную точку В в сторону северного полюса Земли PN. Поскольку судно находится в северном полушарии и движется в сторону северного полюса Земли, то этот специальный чертеж для вывода формулы по вычислению  принято называть «северным чертежом», на котором наглядно видно: чтобы получить дугу
принято называть «северным чертежом», на котором наглядно видно: чтобы получить дугу  , необходимо из дуги
, необходимо из дуги 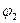 вычесть дугу
вычесть дугу 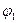 . Поэтому глядя на «северный чертеж» делают безошибочную запись:
. Поэтому глядя на «северный чертеж» делают безошибочную запись:
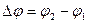 (7.1)
(7.1)
 Поскольку формула (7.1) применима только в том случае, если судно находится в северном полушарии и движется в сторону северного полюса Земли, то необходимо эту формулу преобразовать в алгебраическую формулу, чтобы получить универсальную формулу по вычислению
Поскольку формула (7.1) применима только в том случае, если судно находится в северном полушарии и движется в сторону северного полюса Земли, то необходимо эту формулу преобразовать в алгебраическую формулу, чтобы получить универсальную формулу по вычислению  в любой ситуации, когда начальная и конечная точки пути судна могут находиться в любом полушарии (от лат. universalis –общий, всеобщий):
в любой ситуации, когда начальная и конечная точки пути судна могут находиться в любом полушарии (от лат. universalis –общий, всеобщий):
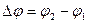
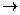
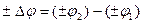 (7.2)
(7.2)
Порядок построения специального чертежа для вывода формулы по вычислению 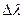 (рисунок 7.2):
(рисунок 7.2):
1. Вычерчивают окружность, которая является земным экватором.
2. Через центр окружности О проводят вертикальную линию 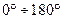 , которая является линией пересечения плоскости гринвичского (нулевого) и демаркационного (сто восьмидесятого) меридианов с плоскостью земного экватора.
, которая является линией пересечения плоскости гринвичского (нулевого) и демаркационного (сто восьмидесятого) меридианов с плоскостью земного экватора.
3. Под углом примерно 60º к линии О - 0º проводят радиус окружности ОА, который является линией пересечения плоскости меридиана точки А с плоскостью земного экватора. Таким образом, угол между линией О - 0º и линией ОА является двугранным углом между плоскостью гринвичского меридиана и плоскостью меридиана точки А и поэтому этот угол обозначают дугой со стрелкой и подписывают 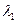 .
.
4. Под углом примерно 120º к линии О - 0º проводят радиус окружности ОВ, который является линией пересечения плоскости меридиана точки В с плоскостью земного экватора и поэтому угол между линией О - 0º и линией ОВ обозначают дугой со стрелкой и подписывают 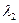 .
.
5. Дугу земного экватора АВ обозначают стрелкой, которая показывает направление движения судна из начальной точки А в конечную точку В в сторону востока. Поэтому дугу АВ подписывают 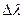 .
.
Таким образом, на рисунке 7.2 изображено экваториальное сечение земного шара, на котором судно находится в восточном полушарии и движется в сторону востока. Поэтому этот специальный чертеж для вывода формулы по вычислению 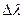 принято называть «восточным чертежом». Глядя на этот чертеж, безошибочно делают запись:
принято называть «восточным чертежом». Глядя на этот чертеж, безошибочно делают запись:
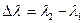 (7.3)
(7.3)
Формулу (7.3) преобразуют в алгебраическую формулу:
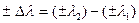 (7.4)
(7.4)
Необходимость соблюдения установленной последовательности вычисления  и
и 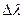 с целью исключения промаха в расчетах и необходимость проверки полученного результата вычисления с помощью чертежа рассмотрим на примере вычисления
с целью исключения промаха в расчетах и необходимость проверки полученного результата вычисления с помощью чертежа рассмотрим на примере вычисления  и
и 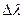 в задаче 7.6:
в задаче 7.6:
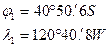
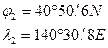
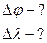
1. Если пренебречь выводом формул по вычислению  и
и 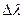 с помощью «северного чертежа» и «восточного чертежа» и записать эти формулы по памяти, то возможна ошибка в написании формул, которая повлечет за собой неправильное определение наименований
с помощью «северного чертежа» и «восточного чертежа» и записать эти формулы по памяти, то возможна ошибка в написании формул, которая повлечет за собой неправильное определение наименований  и
и 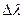 , что является грубейшей ошибкой:
, что является грубейшей ошибкой:
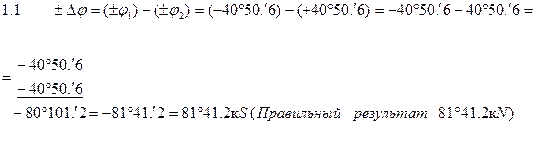
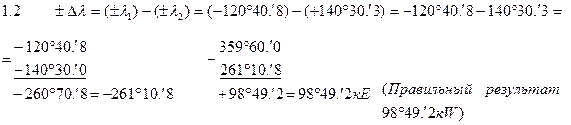
 Таким образом, из-за неправильного написания формул – значения
Таким образом, из-за неправильного написания формул – значения  и
и 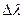 вычислены с грубейшей ошибкой, которую можно выявить с помощью «проверочного чертежа».
вычислены с грубейшей ошибкой, которую можно выявить с помощью «проверочного чертежа».
Порядок построения «проверочного» чертежа после вычисления разности широт двух точек (рисунок 7.3):
1. Вычерчивают меридиональное сечение земного шара по методике, изложенной при построении «северного чертежа».
2. Для удобства и ускорения проверки правильности вычисления  - заданные значения
- заданные значения 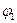 и
и 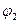 , а так же полученный при вычислении результат
, а так же полученный при вычислении результат  - округляют до одного градуса (1º):
- округляют до одного градуса (1º):
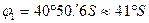 ,
,
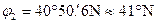 ,
,
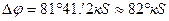
3. От линии OQ в сторону южного полюса Земли РS откладывают на глаз (без транспортира) угол 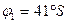 .
.
4. От линии OQ в сторону северного полюса Земли РN на глаз откладывают угол 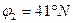 .
.
5. Дугу АВ, которая опирается на суммарный угол 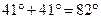 обозначают стрелкой, которая показывает направление движения судна из начальной точки А в конечную точку В в сторону северного истинного полюса Земли РN. Поэтому дугу АВ подписывают:
обозначают стрелкой, которая показывает направление движения судна из начальной точки А в конечную точку В в сторону северного истинного полюса Земли РN. Поэтому дугу АВ подписывают: 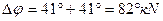 .
.
Таким образом, «проверочный чертеж» не подтвердил правильность вычисления разности широт двух точек с помощью формулы, т.к. согласно этому чертежу наименование разности широт получается «к северу» (кN), а по результатам вычисления – наименование этой разности широт получилось «к югу» (кS).
Порядок построения «проверочного» чертежа после вычисления разности долгот двух точек (рисунок 7.4):
1.Вычерчивают экваториальное сечение земного шара по методике, изложенной при построении «восточного чертежа».
 2. Округляют заданные значения
2. Округляют заданные значения 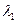 , а так же полученный при вычислении результат
, а так же полученный при вычислении результат 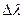 до одного градуса (1º):
до одного градуса (1º):
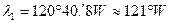
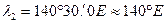
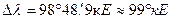
3. От линии 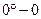 в сторону запада откладывают на глаз угол
в сторону запада откладывают на глаз угол 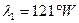 , проводят радиус ОА и подписывают угол:
, проводят радиус ОА и подписывают угол: 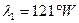 .
.
4. От линии 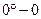 в сторону востока откладывают на глаз угол
в сторону востока откладывают на глаз угол 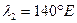 , проводят радиус ОВ и подписывают угол:
, проводят радиус ОВ и подписывают угол: 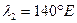 .
.
5. Меньшую дугу экватора АВ обозначают стрелкой, которая показывает направление движения судна из начальной точки А в конечную точку В в сторону запада, т.к. по мере движения судна вдоль земного экватора западного полушария – западная долгота места судна увеличивается от 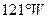 до
до 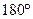 , а после пересечения сто восьмидесятого меридиана, восточная долгота места судна уменьшается от
, а после пересечения сто восьмидесятого меридиана, восточная долгота места судна уменьшается от 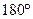 до
до 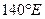 . Поэтому дугу АВ подписывают:
. Поэтому дугу АВ подписывают: 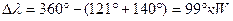 .
.
Таким образом, «проверочный чертеж» не подтвердил правильность вычисления разности долгот двух точек с помощью формулы, т.к. согласно этому чертежу наименование разности долгот получается «к западу» (кW), а по результатам вычисления – наименование этой разности долгот получилось «к востоку» (кЕ).
Неправильное применение «правила знаков» во время раскрытия скобок алгебраической формулы может быть при мысленном раскрытии скобок этой формулы, когда в нарушении необходимой последовательности производства вычисления  и
и 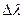 – заданные значения
– заданные значения 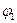 и
и 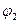 , а так же
, а так же 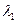 и
и 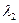 предварительно в скобках не заключают:
предварительно в скобках не заключают:
1. Необходимо соблюдать следующую последовательность вычисления разности широт: 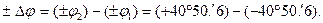 В этом случае обеспечена наглядность выполнения «правила знаков» при раскрытии скобки –
В этом случае обеспечена наглядность выполнения «правила знаков» при раскрытии скобки – 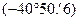 : «минус на минус дает плюс». Поэтому последующие записи в ходе вычисления производят безошибочно:
: «минус на минус дает плюс». Поэтому последующие записи в ходе вычисления производят безошибочно: 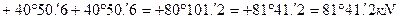 .
.
2. Если в нарушение необходимой последовательности вычисления  значения
значения 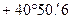 и
и 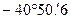 предварительно в скобки не заключать, то отсутствие наглядности применения «правила знаков» во время раскрытия скобок может вызвать ошибочное выполнение этого правила:
предварительно в скобки не заключать, то отсутствие наглядности применения «правила знаков» во время раскрытия скобок может вызвать ошибочное выполнение этого правила:
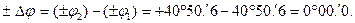
В этом случае «проверочный чертеж» (рисунок 7.3) не подтвердит правильность вычисления  .
.
Аналогично возможно неправильное применение «правила знаков» при мысленном раскрытии скобок алгебраической формулы по вычислению разности долгот двух точек:
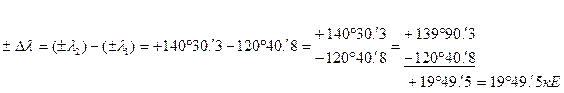
В этом случае «проверочный» чертеж (рисунок 7.4) не подтвердит правильность вычисления 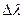 .
.
Таким образом, процедура заключения в скобки алгебраической формулы заданных значений 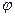 и
и 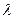 необходима для обеспечения наглядности применения «правила знаков» во время раскрытия скобок этой формулы с целью исключения возможной ошибки выполнения этого правила. Невыполнение этой процедуры не следует мотивировать необходимостью быстрого вычисления
необходима для обеспечения наглядности применения «правила знаков» во время раскрытия скобок этой формулы с целью исключения возможной ошибки выполнения этого правила. Невыполнение этой процедуры не следует мотивировать необходимостью быстрого вычисления  и
и 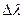 , т.к. быстрота штурманских расчетов достигается отработкой навыков вычисления. Сокращение времени вычисления за счет исключения каких-либо промежуточных звеньев в общей цепи последовательных действий квалифицируется как ненужная торопливость, неуместная для штурманских расчетов, т.к. ошибки, допущенные при решении навигационных задач чреваты тяжелыми последствиями.
, т.к. быстрота штурманских расчетов достигается отработкой навыков вычисления. Сокращение времени вычисления за счет исключения каких-либо промежуточных звеньев в общей цепи последовательных действий квалифицируется как ненужная торопливость, неуместная для штурманских расчетов, т.к. ошибки, допущенные при решении навигационных задач чреваты тяжелыми последствиями.
КРИВИЗНА ЗЕМНОГО ЭЛЛИПСОИДА

 Кривизна земного эллипсоида – это величина, которая характеризует отклонение поверхности этого эллипсоида от касательной плоскости Н-Н в точке наблюдателя (рисунок 8.1). Равноудаленные во всех направлениях от наблюдателя А точки эллипсоида неравномерно отклонены от касательной плоскости Н-Н. Поэтому общую кривизну земного эллипсоида в окрестности точки А определяют средним значением кривизны по главным направлениям N-S и E-W. Таким образом, для определения кривизны земного эллипсоида в точке А необходимо определить кривизну меридианного сечения PNAQPSE и кривизну сечения по первому вертикалу АВСD.
Кривизна земного эллипсоида – это величина, которая характеризует отклонение поверхности этого эллипсоида от касательной плоскости Н-Н в точке наблюдателя (рисунок 8.1). Равноудаленные во всех направлениях от наблюдателя А точки эллипсоида неравномерно отклонены от касательной плоскости Н-Н. Поэтому общую кривизну земного эллипсоида в окрестности точки А определяют средним значением кривизны по главным направлениям N-S и E-W. Таким образом, для определения кривизны земного эллипсоида в точке А необходимо определить кривизну меридианного сечения PNAQPSE и кривизну сечения по первому вертикалу АВСD.
Кривизна меридианного сечения в точке А – это величина, которая характеризует отклонение этого меридианного сечения от касательной прямой в точке А (рисунок 8.4).
Если начало прямоугольных координат поместить в центре симметрии земного эллипсоида О (рисунок 8.2) и сравнить равные по длине ду́ги меридианного эллипса 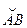 на полюсе Земли и
на полюсе Земли и 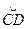 на земном экваторе, то на рисунке 8.2
на земном экваторе, то на рисунке 8.2
Дата добавления: 2015-06-22; просмотров: 2196;
