Уравнения кинетостатики

Слово «кинетостатика» образовано сочетанием двух греческих слов: kinetos – движение, statos – покой, равновесие. То есть, «кинетостатика» означает «равновесие в движении» или «динамическое равновесие». Уравнения кинетостатики звена механизма, как твердого тела, в векторной форме имеют вид:

, ,

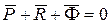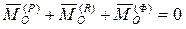Здесь 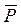, 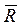- главные векторы активных сил и сил реакций, приложенных к звену, 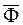- главный вектор сил инерции звена; 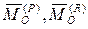- главные моменты активных сил и сил реакций относительно некоторого центра O, 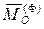- главный вектор сил инерции звена относительно того же центра O. Главный вектор и главный момент сил инерции звена вычисляются по формулам:

, ,

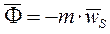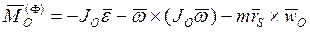где 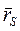- радиус-вектор, 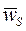- ускорение центра масс, 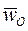- ускорение центра O, m – масса звена; 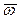- угловая скорость, 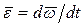- угловое ускорение звена, J_O – тензор инерции звена относительно центра O. Таким образом, в каждый момент времени, действующие на звено силы уравновешиваются силами инерции звена, а моменты сил, приложенные к звену, уравновешиваются моментами сил инерции звена. Это утверждение представляет собой известный из теоретической механики принцип Даламбера, сформулированный по отношению к твердому телу.

В случае плоского механизма, вектор главного момента сил инерции звена относительно центра масс S будет определяться своими декартовыми координатами:

, , .

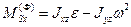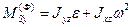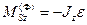В проекциях на оси декартовой системы координат векторные уравнения кинетостатики звена равносильны шести скалярным уравнениям:

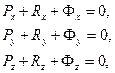
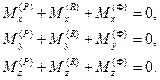
Если механизм плоский и Oxy – плоскость движения звеньев, то три из приведенной системы уравнений становятся тождественно равными нулю и остаются лишь три скалярных уравнения кинетостатики для каждого звена:

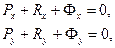
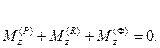
Таким образом, для пространственного механизма требуется составить и решить 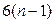, а для плоского - 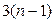скалярных уравнений кинетостатики, где n – число звеньев механизма. Эти системы уравнений могут быть решены аналитически, а в случае плоского механизма векторные уравнения сил удобно решать с помощью метода векторных планов. Для каждого нового положения механизма систему уравнений кинетостатики необходимо составлять и решать заново. Поэтому силовой расчет механизма является довольно трудоемкой задачей, решение которой целесообразно автоматизировать с помощью компьютера.