Дифференциальные уравнения осредненного движения
Для получения уравнений осредненного движения вязкой несжимаемой жидкости Рейнольдс предположил, что действительное движение жидкости, несмотря на его иррегулярность, строго описывается уравнением Навье-Стокса. В результате осреднения всех членов этого уравнения и выполнения необходимых преобразований получим
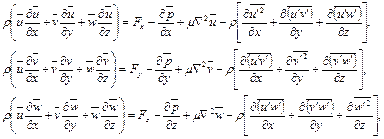 (1.45)
(1.45)
где 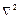 – оператор Лапласа.
– оператор Лапласа.
К этим уравнениям необходимо присоединить уравнение неразрывности для осредненных и пульсационных скоростей
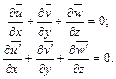 (1.46)
(1.46)
Левые части первой системы трех уравнений формально совпадают с левыми частями уравнений Навье-Стокса для установившегося течения, в правых частях появляются дополнительные члены, обусловленные пульсационным движением.
Граничными условиями для всех уравнений, представленных выше, является равенство нулю на стенках всех составляющих осредненной скорости и всех составляющих пульсационной скорости.
Решение этих уравнений возможно, если известна зависимость между пульсационным и осредненным движениями. Такая зависимость в настоящее время может быть получена только эмпирическим путем. Вид связи между пульсационным и осредненным движениями составляет суть гипотез о турбулентности.
Дата добавления: 2015-01-24; просмотров: 1407;
