Гидравлический удар

Гидравлическим ударом называют резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока жидкости. Он чаще всего возникает при быстром закрытии запорных устройств, внезапной остановке насоса, компрессора и т.п.

Процесс, происходящий в упругом трубопроводе при гидравлическом ударе, носит колебательный характер – быстро протекающее чередование резких повышений и понижений давления. Изменение давления при этом тесно связано с упругими деформациями стенок трубопровода и капельной жидкости, обладающей свойством сжимаемости.

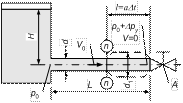
При мгновенном закрытии крана А, установленного в конце трубопровода, по которому движется жидкость со скоростью V₀, частицы ее, натолкнувшиеся на препятствие, останавливаются, и их скорость становится равной нулю. Кинетическая энергия, которой обладали эти частицы переходит в работу деформации стенок трубы и жидкости, в результате чего стенки трубы растягиваются, а жидкость сжимается за счет повышения давления на величину Dp_у. На заторможенные у крана частицы набегают другие, соседние с ними частицы и тоже теряют скорость. В результате этого, сечение "n–n", разделяющее заторможенную и движущуюся области потока, перемещается в направлении, противоположном движению потока, со скоростью а – скоростью ударной волны. Переходная область, в которой происходит изменение давления на некоторую величину Dp_у, называется ударной волной.

Когда ударная волна дойдет до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы – растянутыми. Ударное повышение давления Dp_у распространится на всю длину трубы. Однако такое состояние не является устойчивым. Под действием перепада давления Dp_у частицы жидкости устремятся из трубы в резервуар. С этого момента сечение "n–n" начинает перемещаться в обратном направлении (к крану) с той же скоростью а, оставляя за собой давление p₀. Жидкость и стенки трубы предполагаются упругими, поэтому они возвратятся к исходному состоянию, соответствующему давлению p₀. Работа деформации полностью перейдет в кинетическую энергию, и жидкость в трубе приобретет первоначальную скорость V₀, направленную в противоположную сторону. С этой скоростью жидкая "колонна" стремится оторваться от крана. В результате возникнет отрицательная ударная волна под давление p₀-Dp_у, которая будет двигаться от крана к резервуару со скоростью а, оставляя за собой стенки трубы, испытывающие деформацию сжатия, и жидкость, находящуюся под пониженным давлением. Кинетическая энергия жидкости вновь перейдет в работу деформации, но противоположного знака.

Состояние трубы в момент прихода отрицательной ударной волны к резервуару также не является устойчивым из-за разности давлений в баке и в трубопроводе. Как только отраженная от резервуара ударная волна достигнет крана А, весь цикл гидравлического удара повторится.

Протекание гидравлического удара во времени показано на рис. 1.9, а (штриховые линии соответствуют теоретическому изменению избыточного давления в точке А, сплошные – действительному). Такая картина изменения давления имеет место в случае, когда давление жидкости в трубопроводе до закрытия крана p₀ больше повышения давления в результате гидравлического удара и при снижении давления на величину Dp_у избыточное давление остается положительным.

Рис. 1.9. Изменение давления во времени при гидравлическом ударе

Если давление p₀ невелико, то первоначальное повышение давления при ударе будет примерно таким же, как и в предыдущем случае. Однако снижение давления на величину Dp_у невозможно. Абсолютное давление у крана уменьшится практически до нуля (это соответствует значению разряжения p_вак » -p_б). Это приведет к возникновению кавитации и изменению характеристик колебательного процесса (рис. 1.9, б).

Теория гидравлического удара была разработана профессором Н.Е.Жуковским. Одним из результатов этой теории является формула для определения повышения давления при гидравлическом ударе

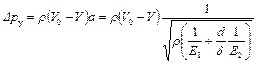, (1.55)

где r – плотность жидкости; V₀ и V –средние скорости движения жидкости до и после закрытия крана; а – скорость распространения ударной волны; Е₁, Е₂ – модули упругости жидкости и материала трубы; d и d – диаметр и толщина трубы.

При полном ( 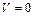) и мгновенном перекрытии потока в трубопроводе возникает максимальное повышение давления.

Формула Жуковского справедлива при очень быстром закрытии крана, когда время закрытия t_з меньше фазы гидравлического удара t₀

.

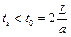При соблюдении этого условия гидравлический удар называют прямым.

В случае, когда возникает непрямой гидравлический удар, при котором ударная волна, отразившись от резервуара, возвращается к крану раньше, чем он будет полностью закрыт. При этом повышение давления в системе Dp_у' меньше, чем при прямом гидравлическом ударе.

При линейном законе изменения скорости в трубопроводе повышение давления при непрямом гидравлическом ударе определяют по формуле

.

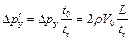Для предотвращения нежелательных последствий гидравлического удара в трубопроводах устанавливают специальные устройства, например, предохранительные клапаны, воздушные колпаки, обеспечивающие расширение пространства, в котором внезапно возбуждается резкое повышение давления. С целью создания условий для непрямого гидравлического удара предусматривают увеличение времени закрытия крана за счет использования резьбы с малым шагом на приводе задвижки.

4.6. Распыление жидкостей /13/

В различных областях техники и технологических процессах используют жидкости, распыленные на мелкие капли. Например, при окраске поверхностей, для увлажнения воздуха в кондиционерах, в многочисленных процессах, где требуется интенсифицировать тепло- и массообмен.

Эффективность работы дизелей в большой степени зависят от правильной организации рабочего процесса, важной составной частью которого является распыление топлива в камере сгорания.

Под распылением топлива понимают совокупность процессов, включающих в себя первичное дробление струи на частицы разных размеров, вторичный распад капель под воздействием аэродинамических сил воздуха, динамику движения распыленной струи и распределение топлива по объему камеры сгорания.

Изучение механизмов процесса распада непрерывных струй, вытекающих с небольшими скоростями (U₁=1¸80 м/с), позволили установить, что поверхность струи подвергается малым возмущениям. Эти возмущения возникают вследствие вихревого движения жидкости, создаваемого трением, колебаниями самого отверстия и отклонениями его геометрии от правильной круглой формы, наличия в струе пылинок и пузырьков воздуха, шероховатости стенок и др.

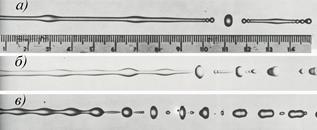
Рис. 1.10. Капиллярная неустойчивость струи жидкости, подверженной возмущениям различной частоты /2/

Под влиянием указанных причин частицы жидкости, находящиеся на поверхности струи, испытывают малые смещения, поверхность струи деформируется и отклоняется от равновесной формы (рис. 1.10). Увеличение свободной энергии поверхности, вызванное подобной деформацией, приводит к появлению капиллярных сил, которые стремятся сократить общую поверхность струи и придать ей равновесную форму. Под действием этих сил частицы жидкости, выведенные из равновесного положения, стремятся вернуться к нему. Однако по инерции они проходят положение равновесия и поэтому вновь испытывают действие восстановительных сил и т.д. В результате таких перемещений на поверхности струи возникают волновые колебания. Эти волны могут распространяться с различными скоростями вдоль струи по направлению ее движения. Амплитуда колебаний в процессе движения волны может либо уменьшаться, либо увеличиваться.

Было замечено, что длина и амплитуда волны колебания увеличиваются прямо пропорционально скорости струи. Если при увеличении скорости длина волны колебания превысит длину окружности невозмущенной струи, то дальнейший рост амплитуды колебания происходит экспоненциально. В результате устойчивость движения струи нарушается, и струя распадается на отдельные части.

Расстояние, проходимое струей за время, необходимое для ее разрушения, определяет длину сплошного участка струи. Эта длина зависит от интенсивности начальных возмущений и характера их развития на поверхности струи после ее выхода из соплового отверстия, от положения струи в пространстве и др.

Разрушение струи как при режиме каплеобразования, так и в случае развития осесимметричных возмущений происходит главным образом под действием сил поверхностного натяжения, сил вязкости и сил тяжести. При движении струи с шероховатой поверхностью усиливается динамическое влияние среды на развитие колебаний. Относительная скорость струи и воздействующей на нее среды увеличивается над выпуклостями и понижается во впадинах, в результате чего давление на гребнях волн уменьшается и растет над впадинами, причем разность между этими давлениями по мере увеличения скорости возрастает. Благодаря этому увеличивается амплитуда колебаний и усиливается неустойчивость движения струи.

В результате наложения и развития возмущений и усиливающегося влияния аэродинамического воздействия окружающей среды поверхность струи подвергается все более сложным деформациям. Возникают колебания, длины волн которых изменяются в широких пределах. Амплитуды этих волн экспоненциально возрастают во времени, что ведет к распаду струи на части различных размеров.

Если скорость струи относительно воздуха значительно повысить, картина ее распада значительно изменится. Вместо распада струи на сравнительно небольшое количество крупных капель происходит ее дробление на многочисленные мелкие частицы, размеры которых меняются в довольно широких пределах. Этот процесс дробления называется распылением.

Выходящая из соплового отверстия струя жидкости в данном случае теряет свою определенную форму, распад ее происходит абсолютно неравномерно. По фотоснимкам и наблюдениям не представляется возможным установить достоверные причины распада струи. Безусловно, на распад в какой-то степени оказывают влияние и внутреннее испарение жидкости (вследствие больших скоростей движения струи статическое давление понижается настолько, что становится близким к давлению насыщения), и завихрение в сопле, вызывающее появление крупномасштабных турбулентных пульсаций, и развитие колебаний различных форм, усиливаемых динамическим воздействием окружающей среды, и др.

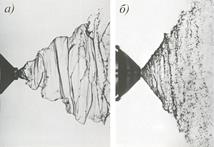
Рис. 1.11. Распыление при истечении жидкости из сопла /2/

Теория распыления, основанная на развитии поверхностных колебаний, учитывает и интенсивные вихреобразования, изотропные и неизотропные крупномасштабные турбулентные пульсации, наличие кавитации. Появление в сопловом отверстии незатухающих турбулентных пульсаций различных размеров и интенсивных вихреобразований, пузырьков пара и воздуха приводит к возмущению поверхности струи при выходе ее из отверстия и деформации этой поверхности, которая усиливается благодаря аэродинамическому воздействию окружающей среды. С увеличением скорости истечения интенсивность возмущений возрастает настолько, что отрыв частиц жидкости начинается непосредственно у соплового отверстия (рис. 1.11). Не распавшийся участок струи благодаря этому окружен большим числом капель, создающих начало распыленной струи жидкости, имеющей форму конуса.

Давление впрыска меняется в период подачи топлива в системах с механическим приводом и движение жидкости через форсунку является неустановившимся. При этом первые части струи получаются более раздробленными, чем следующие непосредственно за ними. Это объясняется моментальным дросселированием топлива при начале подъема иглы форсунки и резким изменением давления при поступлении топлива из камеры форсунки в камеру распылителя, что приводит к возникновению интенсивных начальных возмущений.

Теоретические исследования устойчивости и распада жидких струй основываются главным образом на методе малых возмущений.

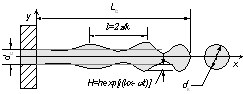
Рис. 1.12. Схема осесимметричной деформации струи

Различные условия движения описываются дифференциальными уравнениями движения жидкости (частными случаями уравнения Навье-Стокса) и уравнением неразрывности, при соответствующих граничных условиях. Обозначим продольную составляющую скорости через u, радиальную через v. Тогда в цилиндрической системе координат уравнения движения вязкой несжимаемой и невесомой жидкости симметрично оси x запишутся в виде

;

,

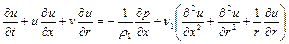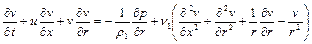а уравнение неразрывности

.

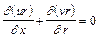При исследовании параметры основного движения заменяют суммами параметров исследуемого течения и наложенных возмущений (u=U₁+u₁; v=v₁; p=p¢+p₁, где U₁ и p¢ – постоянные величины). В полученных уравнениях отбрасывают слагаемые, содержащие произведения параметров возмущенного движения и их производные (линеаризуют уравнения). Затем рассматривают вид поля малых возмущений, отвечающий частному решению полученных линеаризованных дифференциальных уравнений, в котором в качестве множителя входит функция е^iwt, содержащая время t и комплексную частоту колебаний w. Дальнейшая задача сводится к решению обыкновенного дифференциального уравнения, удовлетворению граничных условий и исследованию полученного характеристического уравнения.

В качестве граничных условий при анализе развития малых колебаний на цилиндрической поверхности струи можно принять следующие:

× на оси трубы возмущенное движение отсутствует;

× скорость перемещения поверхности раздела должна быть равной радиальной составляющей скорости струи при r=d_c/2;

× без учета влияния окружающей среды касательное напряжение на поверхности струи равно нулю;

× нормальное напряжения струи должно уравновешиваться давлением поверхностного натяжения.

На границе раздела струи и окружающей среды действуют силы поверхностного натяжения, величина которых зависит от формы деформации и физических свойств топлива. Поверхностная сила, действующая на единицу площади струи, определяется по формуле Лапласа:

,

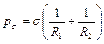где R₁ и R₂ – главные радиусы кривизны в данной точке поверхности.

При малых деформациях поверхности значение поверхностной силы можно представить в виде

,

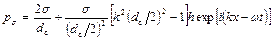где d_c – диаметр отверстия сопла; s – коэффициент поверхностного натяжения; k – волновое число ( ).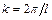

В результате решения дифференциального уравнения при этих граничных условиях получают характеристическое уравнение, устанавливающее связь между частотой колебаний w и всеми параметрами. Точное решение уравнений, описывающих развитие возмущений с произвольной амплитудой, в настоящее время затруднено, поэтому, как правило, рассматриваются эти уравнения применительно к волновым возмущениям с малыми амплитудами h.

Вопрос об устойчивости решается по знаку мнимой части множителя w. Если мнимая часть этого множителя отрицательна, то движение струи считается неустойчивым, так как амплитуда такого вида возмущений растет со временем. И, наоборот, при положительной мнимой части множителя w движение струи будет устойчивым.

Для установления самого факта неустойчивости нужно проанализировать хотя бы одно частное решение, соответствующее неустойчивой деформации, амплитуда которой увеличивается со временем. Наибольшей неустойчивостью по сравнению со всеми другими возмущениями обладают колебания с максимальной частотой. Для нахождения этой частоты надо исследовать характеристическое уравнение на максимум.

Решающее значение для распада струи, согласно Релею, имеет оптимальная длина волны l_опт и соответствующая ей максимальная частота колебаний. Если считать, что капли образуются из части струи, заключенной в объеме длины волны, соответствующей максимальной неустойчивости, то для определения максимального размера капель справедливо выражение

.

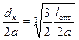Для определения длины не распавшегося участка струи L_c приравнивают время движения жидкости по цилиндрическому каналу длиной L_c с постоянной скоростью U₁, ко времени, в течение которого отклонение возмущенной поверхности над невозмущенной достигает некоторого критического значения.

При расчетах характеристик процесса распыливания (длины сплошного участка струи L_c, среднего диаметра капель d_к, длины волны l_опт, соответствующей наибольшей неустойчивости струи, приводящей к ее дроблению, границ различных режимов распада струи) пользуются следующими безразмерными величинами:

,

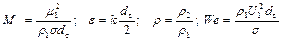где m₁ – коэффициент динамической вязкости топлива; r₁ – плотность топлива; r₂ – плотность воздуха; s – коэффициент поверхностного натяжения топлива; d_c –диаметр отверстия сопла; k – волновое число; We – критерий Вебера; U₁ – осевая скорость движения жидкости в струе.

Теоретические и экспериментальные исследования неустойчивости движения вязкой струи при больших относительных скоростях топлива и воздуха, выполнены А.С.Лышевским. Ниже приведены полученные им результаты.

Граница области перехода от волнообразного распада струи к распыливанию (граничное значение критерия Вебера W_г3, превышение которого обеспечивает распыл) для форсунок с цилиндрическими сопловыми отверстиями при отсутствии внутри них специальных устройств, возмущающих проходящую жидкость, описывается уравнением

.

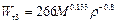На процесс распада струи оказывает значительное влияние скорость истечения, вязкость топлива и среда, в которую происходит его впрыск.

При малых скоростях истечения топлив значение e < 1. Для 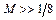пользуются следующими зависимостями:

× для определения длины сплошного участка струи

;

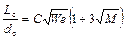× для определения диаметра капель, образующихся при распаде струй из:

топлив с пренебрежимо малой вязкостью

;

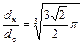маловязких топлив

;

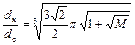топлив большой вязкости

.

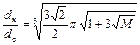При больших скоростях истечения значение e >> 1. Распад струи маловязкого топлива происходит, главным образом, под воздействием коротковолновых возмущений, максимальная частота которых соответствует значению

.

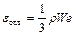Для таких условий расчет ведут по формулам:

,

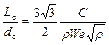где С – эмпирический коэффициент (С=12);

.

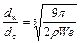При промежуточных значениях скорости истечения маловязкого топлива развиваются осесимметричные возмущения, которые приводят к распаду струи при значении параметра e_опт, равном

.

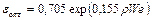В этом случае, длину сплошной части струи рассчитывают по формуле

,

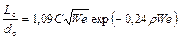где С – эмпирический коэффициент (С=12),

а диаметр капель – по зависимости

.

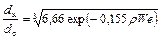Основное влияние на параметры распада струи вязкого топлива при значительных скоростях движения оказывают силы инерции, характеризуемые критериями r и We. Силы вязкости играют второстепенную роль. В предположении об отсутствии поперечного потока воздуха и волнообразных несимметричных возмущений расчет ведут по следующим зависимостям:

,

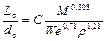где С – эмпирический коэффициент (С=372);

.

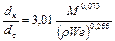Они показывают, что основное влияние на параметры распада струи вязкого топлива при значительных скоростях движения оказывают силы инерции, характеризуемые критериями r и We. Силы вязкости топлив, обычно применяемых в транспортных дизелях, играют второстепенную роль. Поэтому показатель степени у критерия М, в который входит вязкость топлива, небольшой.