Гидравлический расчет трубопроводов

Трубопровод называют простым, если он не имеет ответвлений. Простые трубопроводы соединяют в последовательные, параллельные или разветвленные линии. Сложные трубопроводы содержат как последовательные, так и параллельные соединения или разветвления.

Жидкость движется по трубопроводу, если ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может быть создан либо работой насоса, либо разностью уровней жидкости в начальном и конечном сечениях трубопровода, либо давлением газа (в пневматических системах).

Под гидравлическим расчетом понимают определение параметров движения жидкости при заданной схеме трубопровода с известными конструкционными элементами, либо определение размеров трубопровода, обеспечивающих необходимые параметры движения жидкости.

Простой трубопровод постоянного сечения

Рассмотрим простой трубопровод длиной l, постоянного диаметра d, который содержит ряд местных сопротивлений. Скорость потока в начальном и концевом сечениях одинакова.

Уравнение Бернулли для сечений 1 и 2 имеет вид

,

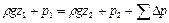или

.

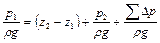Вводя обозначения:

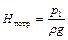× – потребный (располагаемый) напор;

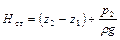× – статический напор;

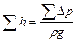× – потери напора,

получим

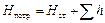, (1.52)

что потребный напор складывается из статического напора (геометрической высоты, на которую поднимается жидкость в процессе движения и пьезометрической высоты в конце трубопровода) и суммы всех потерь напора в трубопроводе.

Потери напора определяют как сумму всех потерь в местных сопротивлениях и потерь, связанных с трением при движении жидкости

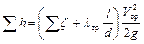, (1.53)

где 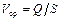– средняя скорость движения среды по трубопроводу; Q – объемный расход жидкости; S – площадь поперечного сечения трубопровода.

При анализе систем используют графики зависимости потребного напора от расхода [H_потр=f(Q)], которые называют кривыми потребного напора, либо графики зависимости суммарной потери напора от расхода [Sh=f(Q)], которые называют характеристиками трубопровода. Характеристика трубопровода – это кривая потребного напора, смещенная в начало координат.

Сифонный трубопровод

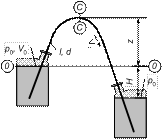Сифонный трубопровод (сифон) представляет собой короткий трубопровод, движение в котором происходит самотеком по всей его длине, включая участки, расположенные выше уровня жидкости питающего резервуара.

Движение жидкости в сифоне происходит под действием атмосферного давления при наличии вакуума в самой верхней точке трубопровода. Поэтому для поднятия жидкости на некоторую высоту или для переливания ее в приемный резервуар необходимо создать в сифоне разряжение (вакуум). С этой целью сифон предварительно заполняют переливаемой жидкостью или откачивают из него воздух при помощи вакуум-насосов.

Гидравлический расчет сифонов заключается в определении расхода жидкости и предельной величины возвышения трубопровода над уровнем жидкости в расходном баке, при котором этот расход обеспечивается.

Расход жидкости, переливаемой сифоном, равен

,

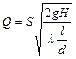где S – площадь поперечного сечения трубопровода; H – разность уровней жидкости в резервуарах; l – коэффициент потерь на трение; l и d – длина и диаметр сифонного трубопровода, соответственно.

Допустимая высота наивысшей точки сифона определяется из уравнения Бернулли, которое записывают для точек, находящихся на свободной поверхности питающего резервуара и в наивысшем удаленном сечении сифона

.

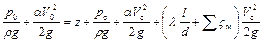При скорости перемещения свободной поверхности жидкости в питающем резервуаре близкой к нулю и коэффициенте кинетической энергии равном единице, получим

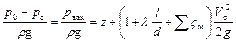
или

.

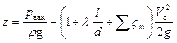Соединения простых трубопроводов

Последовательное соединениенескольких простых трубопроводов различного диаметра дает простой трубопровод переменного сечения.

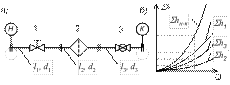
Рис. 1.5. Последовательное соединение трубопроводов

а – схема трубопровода; б – характеристика трубопровода

При подаче жидкости по такому трубопроводу расход во всех последовательно соединенных трубах один и тот же. Полная потеря напора между начальным и конечным сечениями равна сумме потерь напора во всех последовательно соединенных трубах. Для трубопровода, изображенного на рис. 1.5, получим следующие уравнения:

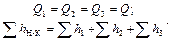
Эти уравнения определяют правило построения характеристик последовательного соединения труб. При известных характеристиках трубопроводов 1, 2 и 3, для получения характеристики их последовательного соединения (участка между сечениями Н и К) следует сложить потери напора при одинаковых расходах, т.е. сложить ординаты всех трех кривых при одних и тех же значениях, выбранных на оси абсцисс.

В начальном и конечном сечениях рассматриваемого трубопровода скорости движения жидкости различны. Поэтому выражение потребного напора для всего трубопровода должно содержать разности скоростных напоров в крайних сечениях.

.

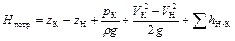Параллельное соединение нескольких простых трубопроводов показано на рис. 1.6.

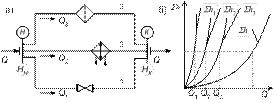
Рис. 1.6. Параллельное соединение трубопроводов

а – схема трубопровода; б – характеристика трубопровода

Обозначим полные напоры в точках Н и К соответственно через H_Н и H_К, расход в основной магистрали (до разветвления и после слияния) – Q, а в параллельных трубопроводах через Q₁, Q₂, и Q₃; суммарные потери напора в этих трубопроводах через Sh₁, Sh₂ и Sh₃.

Расход в основной магистрали связан с расходами в параллельных трубопроводах следующим очевидным уравнением

.

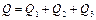Потери напора в каждом из трубопроводов представляют собой разность напоров в точках Н и К

.

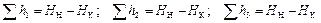Из этого следует, что потери напора в параллельных трубопроводах равны между собой

.

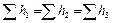Используя уравнение, связывающее расходы в магистральном и параллельных трубопроводах, равенство потерь напора в них, а также соотношения для расчета простых трубопроводов, получим число уравнений, достаточное для определения сопротивлений параллельных вервей и расходов в них.

Из вышесказанного следуют правило построения характеристики параллельного соединения нескольких трубопроводов: суммарная характеристика получается в результате сложения абсцисс характеристик отдельных трубопроводов (Q_i) при одинаковых ординатах (Sh).

Изложенные соотношения для параллельных трубопроводов справедливы и в том случае, когда трубопроводы не сходятся в одной точке, а подают жидкость в различные места, но с одинаковыми давлениями и равными уровнями. Если последнее условие не соблюдается, то рассматриваемые трубопроводы нельзя читать параллельными, а следует отнести к разряду разветвленных.

Разветвленное соединение – это совокупность нескольких простых трубопроводов, имеющих одно общее сечение – место разветвления (или смыкания) труб. Рассмотрим основной трубопровод, который в точке М разделяется на несколько трубопроводов, имеющих различные размеры, местные сопротивления, уровни и давления в концевых точках. Найдем связь между давлением в точке М и расходами в ответвлениях, считая направления течения в них заданными.

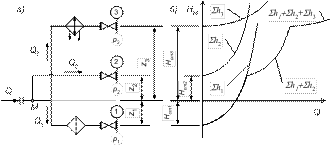
Рис. 1.7. Разветвленный трубопровод

а – схема трубопровода; б – кривые потребного напора

Запишем, пренебрегая динамическими напорами, уравнения Бернулли для каждого из ответвлений, начинающихся в точке М

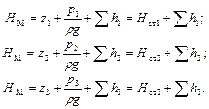
Так же как и для параллельных трубопроводов,

.

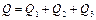Таким образом, получаем систему четырех уравнений достаточную для определения неизвестных величин: Q₁, Q₂, Q₃ и H_м.

Построение кривой потребного напора для разветвленного трубопровода выполняют сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов – сложением абсцисс (Q) при одинаковых ординатах (H_м). Из графика (рис. 1.7, б) видно, что условием подачи жидкости во все ветви является превышение напора в точке разветвления над наибольшим статическим напором в ответвлениях.

Сложный трубопровод состоит из простых трубопроводов с последовательным и параллельным их соединением или с разветвлениями.

При расчетах сложных трубопроводов их разбивают на простые участки, участки с разветвлениями и параллельными трубопроводами и, идя от конечных точек сложного трубопровода к начальной его точке, т.е. против течения, последовательно производят расчеты по приведенным выше уравнениям.

Для сложных кольцевых трубопроводов (системы смежных замкнутых контуров с отборами жидкости в узловых точках или непрерывной раздачей ее на отдельных участках) используют два основных условия:

× баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки;

× баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого контура при подсчете по направлению движения часовой стрелки. Потери напора считают положительными, если направление подсчета совпадает с направлением движения жидкости, и отрицательными, если направление подсчета противоположно направлению движения жидкости.

Трубопроводы с насосной подачей жидкости

В машиностроении основным является способ принудительной подачи жидкости насосом. Рассмотрим совместную работу насоса с трубопроводом и принцип расчета таких систем.

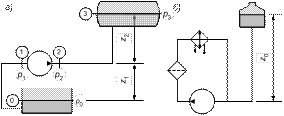
Рис. 1.8. Трубопровод с насосной подачей

Трубопровод с насосной подачей может быть разомкнутым, когда жидкость перекачивается из одной емкости в другую или замкнутым, в котором циркулирует одно и то же количество жидкости.

На рис. 1.8, а представлен разомкнутый трубопровод, по которому жидкость перекачивается насосом из нижнего резервуара с давлением p₀ в другой резервуар с давлением p₃. Высоту расположения оси насоса относительно нижнего уровня z₁ называют геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом (линией всасывания). Высоту расположения верхнего уровня жидкости z₂, называют геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным (линией нагнетания).

Составим уравнение Бернулли для потока жидкости во всасывающем трубопроводе, т.е. для сечений 0 и 1

.

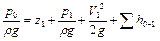Данное уравнение является основным для расчета всасывающих трубопроводов. Оно показывает, что процесс всасывания, т.е. подъем жидкости на высоту z₁, сообщение ей кинетической энергии и преодоление всех гидравлических сопротивлений происходит за счет использования (с помощью насоса) давления p₀. Так как это давление обычно бывает весьма ограниченным, то расходовать его надо так, чтобы перед входом в насос остался некоторый запас давления p₁, необходимый для его нормальной бескавитационной работы.

Уравнение Бернулли для движения жидкости по напорному трубопроводу, т.е. для сечений 2 и 3

.

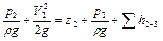Левая часть уравнения представляет собой энергию жидкости на выходе из насоса, отнесенную к единице веса.

Энергия потока перед входом в насос может быть вычислена из уравнения всасывающего трубопровода

.

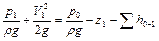Приращение энергии каждой единицей веса жидкости в насосе называют напором, создаваемым насосом H_нас. Он равен

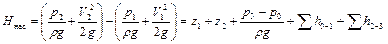
или

,

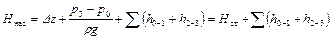где 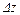– разность уровней жидкости в расходном и приемном баках.

Сравнения полученной формулы с зависимостью для определения потребного напора позволяет сформулировать правило: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному

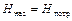. (1.54)

На этом правиле основывается метод расчета трубопроводов, питаемых насосом, заключающийся в определении точки пересечения характеристики насоса и кривой потребного напора трубопровода. Эта точка получила название рабочей точки.

Для замкнутого трубопровода (рис. 1.8, б) геометрическая высота подъема жидкости равна нулю (Dz=0), следовательно, при равенстве скоростей на входе и выходе из насоса (V₁=V₂)

,

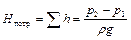т.е. между потребным напором и напором, создаваемым насосом, справедливо то же равенство.

Замкнутый трубопровод обязательно должен иметь расширительный, или компенсационный бачок, соединенный с одним из сечений трубопровода, чаще всего со стороны всасывания насоса, где давление имеет минимальное значение. Он служит для компенсации утечек и предотвращения колебания давления в системе, связанных с изменением температуры.

При наличии расширительного бачка, присоединенного в соответствии с рис. 1.8, б, давление на входе в насос определится из выражения:

.

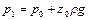По величине p₁ можно подсчитать давление в любом сечении замкнутого трубопровода. Если давление в бачке изменить на некоторую величину, то во всех точках данной системы давление изменится на ту же самую величину.