Расчет сопротивления при турбулентном течении жидкости по каналам

Ввиду сложности турбулентного течения и трудности его аналитического исследования до настоящего времени не существует достаточно строгой теории этого процесса. В практических расчетах пользуются экспериментальными данными, систематизированными с помощью теории подобия.

Основной расчетной формулой для потерь давления при турбулентном течении в круглых трубах является формула Дарси-Вейсбаха

.

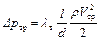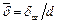Коэффициент потерь на трение при турбулентном течении l_т является функцией критерия Рейнольдса, а также может зависеть от безразмерного геометрического фактора – относительной шероховатости поверхности трубы – отношения средней высоты неровностей поверхности к диаметру трубы . Переход от ламинарного режима течения к турбулентному начинается при некотором критическом значении критерия Рейнольдса Re_кр. При течении жидкости в трубах .

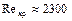На сопротивление шероховатых труб оказывает влияние характер шероховатости. Равномерно распределенная зернистая шероховатость имеет один и тот же размер 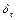и форму бугорков. Получают ее, как правило, искусственным путем.

Исследования, проведенные И.И. Никурадзе, показали, что:

× при ламинарном течении шероховатость стенок канала на сопротивление влияния не оказывает;

× критическое значение критерия Рейнольдса от шероховатости практически не зависит;

× в области турбулентного течения при небольших значениях Re и малых 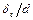шероховатость на сопротивление не влияет. Однако с увеличениемRe это влияние начинает проявляться;

× при большихотносительных шероховатостях и высоких значениях критерия Рейнольдса коэффициент сопротивления перестает зависеть отRe и становится постоянным для данного значения .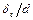

Для труб с реальной шероховатостью вводят понятие эквивалентной абсолютной шероховатости 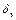т.е. шероховатости, которая оказывает такое же воздействие, что и равномерная зернистая шероховатость в опытах И.И. Никурадзе. У таких труб неровности на поверхности имеют различную высоту и, при увеличении значения критерия Рейнольдса, начинают выступать за пределы ламинарного подслоя не одновременно. Поэтому переход от линии, соответствующей сопротивлению гладких труб, к прямым горизонтальным участкам происходит плавно.

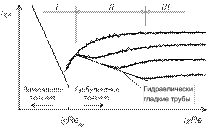
Рис. 1.4. Области влияния шероховатости

а – область гидравлически гладких труб I; б – переходная область II;

в – квадратичная область III

Различают три области влияния шероховатости и числа Рейнольдса на коэффициент потерь на трение:

× область I соответствует гидравлически гладким трубам (цельнотянутым трубам из цветных металлов, а также стальным высококачественным бесшовным трубам, у которых шероховатость не влияет на их гидравлическое сопротивление, поскольку высота бугорков неровностей 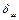не превышает 25% толщины вязкого ламинарного подслоя 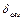турбулентного потока [рис. 1.4, а]). Для этой области, которая определяется диапазоном 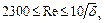, используют формулу Блазиуса

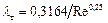; (1.47)

× область II (рис. 1.4, б) наблюдается, когда толщина вязкого ламинарного подслоя имеет тот же порядок величины, что и высота бугорков шероховатости. Для этой переходной области 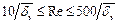применяют формулу А.Д. Альтшуля

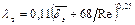; (1.48)

× в области III (рис. 1.4, в) высота бугорков шероховатости больше 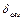, поэтому за ними происходит отрыв потока и интенсивное вихреобразование. Для этой области, называемой квадратичной, 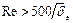, сопротивление не зависит от критерия Рейнольдса. Расчет коэффициента потерь на трение ведут по формуле Б.Л. Шифринсона

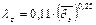. (1.49)

В случае течения жидкости по трубам, форма поперечного сечения которых отличается от круглой, в приведенных выше зависимостях используют эквивалентный диаметр

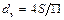, (1.50)

где S – площадь живого сечения канала (сечения, в каждой точке которого направления векторов скорости частиц жидкости перпендикулярны к нему); П – полный смоченный периметр трубы (длина линии контакта живого сечения потока со стенками канала, вдоль которых происходит движение жидкости).

Отношение площади живого сечения потока к смоченному периметру называют гидравлическим радиусом.