Теорема Жуковского

Как известно, динамика одноподвижного механизма с идеальными связями подчиняется принципу Даламбера, который может быть сформулирован в следующем виде:

,

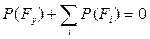где 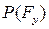- мгновенная мощность уравновешивающей силы, 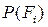- мгновенные мощности активных сил, действующих на механизм, включая силы инерции. В качестве уравновешивающей силы выступает сила, развиваемая приводом механизма.

В случаях, когда ставится задача вычисления только обобщенных движущих сил, проводить трудоемкий расчет по уравнениям кинетостатики нецелесообразно. Если имеются векторные планы скоростей, то определить движущую силу или момент можно методом Жуковского, который основан на принципе Даламбера и теореме Жуковского:

· Мгновенная мощность силы, приложенной к звену, пропорциональна моменту этой же силы относительно полюса повернутого на 90⁰ плана скоростей механизма.

Для доказательства теоремы рассмотрим звено механизма (Рис. 28,а).

Мгновенная мощность силы F определяется равенством:

,

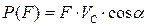где V_C – абсолютная скорость точки С, в которой действует сила.

Момент силы F относительно полюса повернутого на 90⁰ плана скоростей, как видно из рис. 28б, вычисляется по формуле:

.

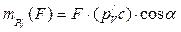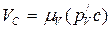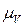Так как , где - масштаб плана скоростей, то окончательно имеем:

,

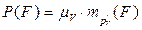что и требовалось доказать.