СТРУКТУРНЫЙ АНАЛИЗ

Рассмотрим исполнительный механизм строгального станка, изображенный на рис. 30. Данный механизм состоит из шести звеньев: стойка 0, кривошип 1, ползушки 2 и 4, кулиса 3, суппорт 5 с установленным на нем резцом. Звенья механизма образуют семь кинематических пар: 0 – 1, 1 – 2, 0 – 3, 3 – 4 – вращательные, одноподвижные, пятого класса; 2 – 3, 4 – 5 – поступательные, одноподвижные, пятого класса; 5 – 0 – цилиндрическая, двухподвижная, четвертого класса. Указанные кинематические пары – низшие; следовательно, рассматриваемый механизм является рычажным. Звенья механизма движутся в плоскостях, параллельных неподвижной плоскости – исследуемый механизм является плоским. Он не содержит звеньев, образующих только одну кинематическую пару; следовательно, является замкнутым. Звенья механизма образуют два замкнутых контура: 0 –1 – 2 –3 – 0 и 0 – 3 – 4 – 5 – 0. Число степеней свободы механизма определим, применяя универсальную формулу Чебышева

,

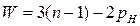где n – число звеньев, p_Н – число низших кинематических пар. В рассматриваемом механизме n = 6, p_Н = 7, поэтому 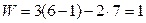- механизм обладает одной степенью свободы. Выявим избыточные связи: кинематическая пара стойка-суппорт, как видно на структурной схеме, имеет ветвление: число избыточных связей типа Б определим по формуле

,

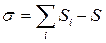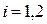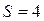где i - индекс ветвления пары, S_i – число независимых связей в i – той ветви, S – класс кинематической пары. Так как в данном случае , (оба ветвления цилиндрические) и (класс цилиндрической пары – четвертый), то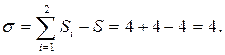

Число избыточных связей, образованных при замыкании контуров (тип В), определим из формулы Малышева

,

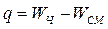где W_Ч – число степеней свободы, найденное по формуле Чебышева, W_СМ – число степеней свободы, найденное по формуле Сомова – Малышева: , i – класс кинематических пар, p_i – число кинематических пар класса . В данном случае и 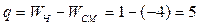. Таким образом, в механизме имеется четыре избыточные связи типа Б и пять избыточных связей типа В.

В соответствии с принципом Ассура, выделим начальный механизм, обладающий числом степеней свободы всего исследуемого механизма. Этот механизм – кривошипный, состоит из стойки 0 и кривошипа 1 (рис. 31). Остальные звенья образуют ведомую цепь, имеющую нулевую подвижность относительно звеньев начального механизма. Ведомая цепь, в свою очередь, состоит из двух двухзвенных структурных групп: 2 – 3 и 4 – 5.

На рис. 2 штриховой линией обозначены внешние кинематические пары – «поводки», которыми звенья групп присоединяются к начальному механизму или к звеньям соседних групп.