Определение движущего момента методом Жуковского

Вычислим движущий момент M, действующий на кривошип 1 в рассматриваемом положении механизма (рис. 36). Ввиду малости сил инерции кулисы 3 по сравнению с другими силами, пренебрежем их величиной. Тогда расположение активных сил на повернутом плане скоростей механизма будет иметь вид (рис. 45).

Уравнение моментов относительно полюса p_v:

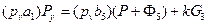Положение точки s₃ на плане скоростей (конец отрезка, изображающего скорость центра масс кулисы 3) определяется на направлении p_vb₃, расстояние от точки p_v до точки s₃ вычисляется по формуле

Плечо k, измеренное на плане скоростей, равно 4 мм. Тогда уравновешивающая сила

Движущий момент, приложенный к кривошипу 1,

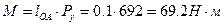что подтверждает правильность расчетов, проведенных в п. 5.1.

Результаты силового анализа механизма в заданном положении приведены в таблице 4.

Таблица 4

P	R₀₁	R₂₁	R₃₂	R₄₃	R₄₅	R₀₃	R₀₅	k	M
Н	м	Н× м
1200	2256.6	2248.1	2248.1	1226.4	1226.4	1152.8	117.7	0.36	71.1

Для того чтобы получить информацию о силах, действующих на звенья механизма за время полного оборота кривошипа, необходимо выполнить все приведенные вычисления для одиннадцати положений механизма.

<23 24 25 262728 29 >

Дата добавления: 2015-03-03; просмотров: 747;