СИЛОВОЙ АНАЛИЗ
Определение неизвестных сил методом векторных планов
Найдем силы реакций в кинематических парах и движущий момент, приложенный к кривошипу 1, для положения механизма, изображенного на рис. 39. Значение силы резания P и параметры звеньев даны в таблице 3.
Таблица 3
| P, кН | h, м | a, м | b, м | c, м | m1, кг | m3, кг | m5, кг | J3, кг∙м2 |
| 1.2 | 0.70 | 0.10 | 0.10 | 0.25 | 5 | 10 | 12 | 0.3 |
На кинематической схеме буквой S с указанием номера звена обозначены центры масс соответствующих звеньев. Массами ползушек 2 и 4, а также силами трения в кинематических парах пренебрегаем.
Рассмотрим выходную группу звеньев 5-4. Выделим суппорт 5, обозначая все действующие на него силы (рис. 40).

Сила инерции суппорта Ф5 приложена в его центре масс и направлена в сторону, противоположную ускорению wB5 (см. план ускорений на рис. 38). Равнодействующая сил тяжести суппорта G5 также приложена в центре масс и направлена вертикально вниз. Сила реакции R45 со стороны ползушки 4 приложена в точке B, так как ползушки имеют малые линейные размеры, и направлена под прямым углом к поверхности, вдоль которой перемещается ползушка 4. Равнодействующая R05 сил реакции стойки направлена под прямым углом к поверхности, вдоль которой перемещается суппорт, но плечо k этой силы относительно центра масс суппорта неизвестно. Проанализировав характер нагрузки на суппорт 5, заключаем, что необходимо определить три неизвестные величины: модули сил реакций R45, R05 и расстояние k. Для этого нам необходимо составить и решить три независимых уравнения кинетостатики звена. Уравнение сил в горизонтальном направлении имеет вид (силы, направленные вправо, учитываются со знаком «+»):
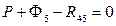 ,
,
откуда 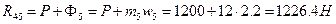 . Уравнение сил в вертикальном направлении (силы, направленные вверх, учитываются со знаком «+»):
. Уравнение сил в вертикальном направлении (силы, направленные вверх, учитываются со знаком «+»):
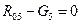 ,
,
откуда 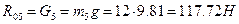 . Уравнение моментов относительно центра масс S5 суппорта (моменты сил, действующие против часовой стрелки, учитываются со знаком «+»):
. Уравнение моментов относительно центра масс S5 суппорта (моменты сил, действующие против часовой стрелки, учитываются со знаком «+»):
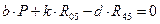 ,
,
откуда 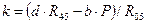 . Плечо d, согласно рис. 11, найдем из соотношения
. Плечо d, согласно рис. 11, найдем из соотношения
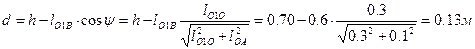 .
.
Соответственно, 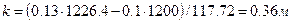 .
.
Теперь перейдем к группе звеньев 2-3. Выделим кулису 3, обозначая все действующие на нее силы (рис. 41).

Сила тяжести кулисы 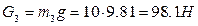 , направлена вертикально вниз. Сила инерции
, направлена вертикально вниз. Сила инерции 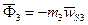 , где
, где 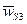 - ускорение центра масс S3 кулисы. Согласно плану ускорений (рис. 38), отрезок
- ускорение центра масс S3 кулисы. Согласно плану ускорений (рис. 38), отрезок 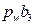 , изображающий полное ускорение точки B кулисы, равен 58 мм. Значение ускорения этой точки определится как произведение длины изображающего отрезка на масштаб плана ускорений:
, изображающий полное ускорение точки B кулисы, равен 58 мм. Значение ускорения этой точки определится как произведение длины изображающего отрезка на масштаб плана ускорений: 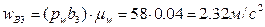 . Тогда ускорение центра масс S3 найдем из пропорции
. Тогда ускорение центра масс S3 найдем из пропорции
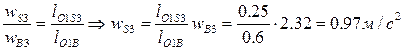 .
.
Абсолютная величина силы инерции кулисы 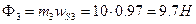 , направление – в сторону, противоположную ускорению центра масс. Момент сил инерции собственного вращения кулисы по абсолютной величине
, направление – в сторону, противоположную ускорению центра масс. Момент сил инерции собственного вращения кулисы по абсолютной величине 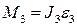 , где
, где 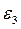 - угловое ускорение кулисы, которое найдем по формуле
- угловое ускорение кулисы, которое найдем по формуле
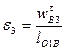 .
.
Из плана ускорений имеем 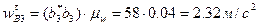 ,
, 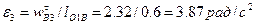 . Тогда
. Тогда 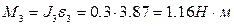 , направление момента сил инерции кулисы – в сторону, противоположную угловому ускорению (рис. 13). Сила реакции R43 со стороны ползушки 4 равна по модулю реакции R45 и направлена в противоположную сторону. Реакция R23 со стороны ползушки 2 направлена перпендикулярно перемещению ползушки 2, но неизвестен ее модуль. Реакция R03 со стороны стойки неизвестна ни по модулю, ни по направлению (на рис. 41 направление этой реакции указано произвольно).
, направление момента сил инерции кулисы – в сторону, противоположную угловому ускорению (рис. 13). Сила реакции R43 со стороны ползушки 4 равна по модулю реакции R45 и направлена в противоположную сторону. Реакция R23 со стороны ползушки 2 направлена перпендикулярно перемещению ползушки 2, но неизвестен ее модуль. Реакция R03 со стороны стойки неизвестна ни по модулю, ни по направлению (на рис. 41 направление этой реакции указано произвольно).
Величину реакции R23 определим из уравнения моментов относительно точки O1:
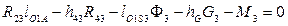 ,
,
откуда 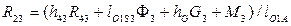 . Плечо силы R43
. Плечо силы R43 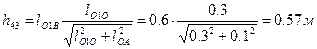 , плечо силы тяжести
, плечо силы тяжести 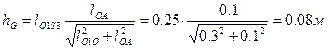 . Следовательно,
. Следовательно, 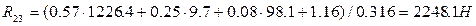 .
.
Реакцию R03 определим путем построения плана сил. Векторное уравнение сил имеет вид
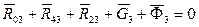 .
.
Пусть реакция R43 отображается на плане отрезком длины 50 мм. Тогда масштаб плана сил 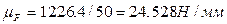 . Отрезок, изображающий реакцию R23:
. Отрезок, изображающий реакцию R23: 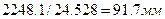 ; отрезки, изображающие силы G3 и Ф3 равны 4 мм и 0.4 мм соответственно. Ввиду малости отрезка, изображающего силу Ф3, пренебрежем в расчете этой силой. План сил, построенный в принятом масштабе, представлен на рис. 42.
; отрезки, изображающие силы G3 и Ф3 равны 4 мм и 0.4 мм соответственно. Ввиду малости отрезка, изображающего силу Ф3, пренебрежем в расчете этой силой. План сил, построенный в принятом масштабе, представлен на рис. 42.
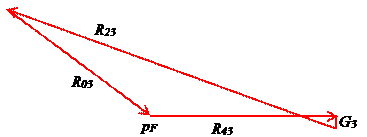
Отрезок, изображающий реакцию R03, равен 47 мм, следовательно, 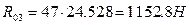 .
.
Рассмотрим начальную группу звеньев «стойка – кривошип». Выделим кривошип 1, обозначая все действующие на него силы (рис. 15).
На кривошип действует сила тяжести 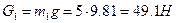 ; реакция со стороны ползушки 2, равная по модулю R23 и направленная в противоположную сторону; реакция со стороны стойки R01, не известная ни по модулю, ни по направлению (на рис. 15 эта реакция обозначена произвольно) и движущий момент M, не известный по величине.
; реакция со стороны ползушки 2, равная по модулю R23 и направленная в противоположную сторону; реакция со стороны стойки R01, не известная ни по модулю, ни по направлению (на рис. 15 эта реакция обозначена произвольно) и движущий момент M, не известный по величине.
Движущий момент M найдем из уравнения моментов относительно точки O:
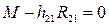 ,
,
где 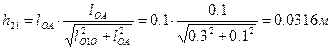 - плечо силы R21 относительно точки O.
- плечо силы R21 относительно точки O.
Получаем 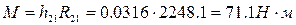 .
.
Реакцию R01 определим, построив план сил. Векторное уравнение сил, действующих на кривошип 1, имеет вид
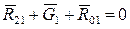 .
.
План сил в масштабе 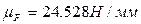 представлен на рис. 44.
представлен на рис. 44.

Отрезок, изображающий на плане реакцию R01, равен 92 мм, следовательно 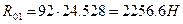 .
.
Дата добавления: 2015-03-03; просмотров: 1011;
