Исследование разрешимости задачи силового анализа в общей постановке

Пусть имеется механизм, состоящий из некоторого числа n звеньев. Предположим, что в данном механизме имеются кинематические пары всех классов. Определим число независимых уравнений, описывающих динамику движения этого механизма. Так как в механизме одно звено неподвижно (стойка), то число подвижных звеньев составит n – 1. Число степеней свободы системы из 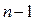твердых тел в трехмерном пространстве равно 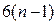, что составляет число независимых уравнений динамики 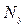. Определим теперь число неизвестных сил и моментов, которые требуется найти. В общем случае в каждой кинематической паре будем иметь три неизвестных силы реакции и три неизвестных момента реакции. Следовательно, общее число неизвестных реакций составит 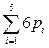, где i - класс кинематической пары, p_i – число кинематических пар класса i. Число неизвестных обобщенных движущих сил равно числу степеней свободы механизма, согласно формуле Сомова – Малышева:

,

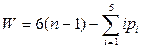тогда общее число неизвестных сил и моментов

.

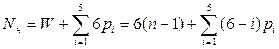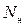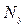Разность чисел и составит

.

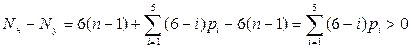Вывод: число неизвестных превышает число независимых уравнений, поэтому задача силового анализа без дополнительных условий, учитывающих особенности конкретного механизма, является неразрешимой.