Віконне перетворення та Вейвлет аналіз

Нестаціонарних сигналів

Розрізняють дискретний і безперервний вейвлет аналіз, апарат яких можна застосовувати як для безперервних, так і для дискретних сигналів.

Сигнал аналізується шляхом розкладання по базисних функціях, одержаних з деякого прототипу шляхом сжатий, розтягувань і зсувів (1.26). Функція-прототип називається аналізуючим (материнським) вейвлетом.

Вейвлет – функція повинна задовольняти 2-м умовам:

1. Середнє значення (інтеграл по всій прямій) рівний 0.

2. Функція швидко убуває при t ®∞.

Звичайно, функция-вейвлет позначається буквою ψ.

У загальному випадку вейвлет перетворення функції f(t) виглядає так:

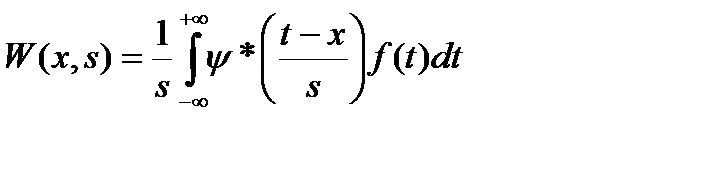(1.26)

де t – вісь часу, x – момент часу, s – параметр, зворотний частоті, а (*) – означає комплексно-зв'язане.

Головним елементом у вейвлет аналізі є функция-вейвлет. Взагалі кажучи, вейвлетом є будь-яка функція, що відповідає двом вищезгаданим умовам.

Отже, у нас є деяка функція f(t), залежна від часу. Результатом її вейвлет-аналізу буде деяка функція W(x, s), яка залежить вже від двох змінних: від часу і від частоти (обернено пропорційно). Для кожної пари x і s рецепт обчислення вейвлет перетворення наступний:

1. Функція вейвлет розтягується в s раз по горизонталі і в 1/s раз по вертикалі.

2. Далі він зсовується в точку x. Одержаний вейвлет позначається ψ(x, s).

3. Проводиться усереднювання в околиці точки s при допомозі ψ(x, s).

Існує два різні шляхи проведення вейвлет перетворення. Йдеться про розрахунки в часовій і частотній областях. При роботі в часовій області ми маємо справу з функціями, аргументами яких є часові параметри, а у разі частотної – частотні. В частотній області використовується механізм швидкого перетворення Фур’є.

У часовій області.

Перш за все, нам необхідно визначити материнський вейвлет. Припустимо, ми вибрали деяку функцію, що задовольняє необхідним умовам: ψ₀(η), де η – безрозмірний період.

Отже, нам дана тимчасова серія X, із значеннями x_n, в моменти часу nÎ[0, N-1], де N – кількість вимірювань. Кожна величина розділена за часом на постійну величину dt. Одержавши основну формулу для материнського вейвлета, необхідно мати нагоду змінювати розміри вейвлета. Для цього будується так званий "масштабувальний" вейвлет який матиме вигляд:

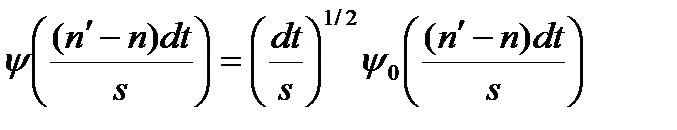(1.27)

s – параметр, зворотний частоті.

Обчислення вейвлет перетворення є звірткою шуканій тимчасовій серії з функцією-вейвлетом. Основна формула має вигляд:

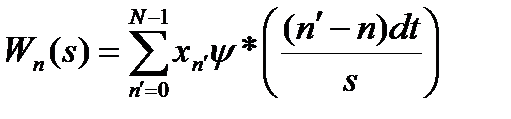. (1.28)

у даному випадку (*) – означає комплексно-зв'язане.

Результатом розрахунку Wn(s) по формулі буде комплексне число. Як кінцевий результат береться абсолютне значення одержаного комплексного числа.

У частотній області.

Вейвлет перетворення можна провести в частотній області. Для цього знову в першу чергу необхідно визначити материнський вейвлет. Розрахунок по даній схемі відбувається таким чином: перетворення Фур’є самого вейвлета (в даному випадку розглядатимемо вейвлет Морле) сконцентровано навкруги деякої виділеної частоти w₀≠0. Тому перетворення Фур’є вейвлета, розтягнутого в s раз, буде сконцентровано навкруги частоти w₀/s .

Оскільки згортка функцій еквівалентна їх перемножуванню в частотній області, “рядок” s = const на зображенні вейвлет перетворення показує еволюцію функції, що вивчається, на частотах, близьких w₀/s. Тобто множення Фур’є-спектру початкової функції на пік в крапці w₀/s в частотній області (тобто на Фур’є-образ розтягнутого вейвлету) вирізує з цієї функції все те, що дає внесок в її спектр на частотах, близьких w₀/s. В результаті виходить розгортка спектрального компоненту в часі.

Основні формули мають вигляд:

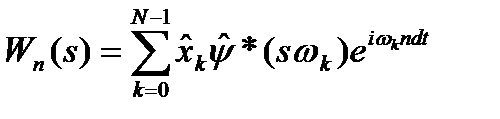(1.29)

де (*) – означає комплексно-зв'язане, а знак (^) – перетворення Фур’є.

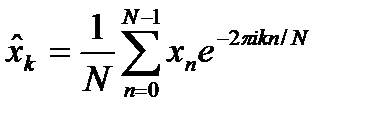(1.30)

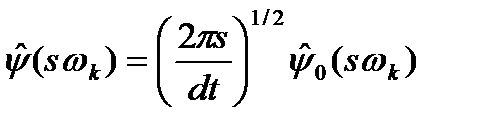(1.31)

Розглянуті методи неприродні для аналізу нестаціонарних процесів, коли потрібна інформація про час виникнення нової складової сигналу. Коли виникає потреба в часовій локалізації спектральних складових сигналу, треба звернутись до частотно-часового представлення у вигляді віконцевого перетворення Фур’є або Вейвлет перетворенні.

Спектральний аналіз включає традиційне Фур'є перетворення, віконцеве Фур'є перетворення та вейвлет перетворення. Пряме перетворення Фур'є використовується для розкладання кривої перехідного процесу F(t), отриманої при моделюванні в області часу, на гармонійні складові і передбачає стаціонарність сигналу, відсутність розривів та стрибків. Спочатку обчислюються значення кривої перехідного процесу для значень:

,

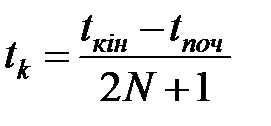де t_поч, t_кін– початок і кінець часового інтервалу перетворень;

N – ціле число, задається користувачем;

k – 1, 2,…, 2N...

Потім за допомогою простого рекурентного методу пряма спочатку апроксимується сумою гармонік:

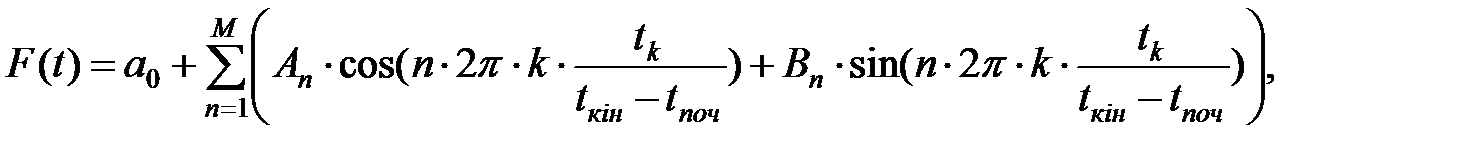
де М – максимальний порядок апроксимуючих гармонік.

Потім перераховуються до виду:

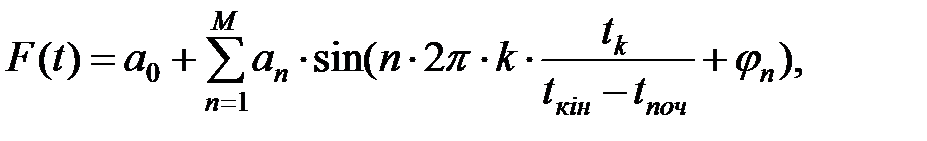(1.32)

де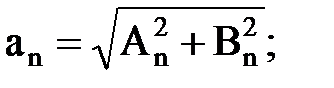

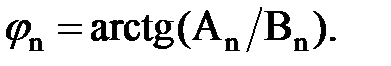
Результати перетворення видаються на друкування у виді таблиці залежності a_n і φ_n від номера апроксимуючої гармоніки.

Спектральний аналіз виконується після розрахунку перехідних характеристик швидким перетворенням Фур’є із розрахунком коефіцієнта нелінійних спотворень. Можна розраховувати частотні характеристики пристроїв, заданих передаточною функцією, але перетворення Лапласа не можна використовувати для завдання лінійних блоків із постійними коефіцієнтами передачі.

Для розрахунку імпульсної характеристики за допомогою перетворення Фур’є в режимі аналізу АС по вісі ОХ задається час, а для побудови годографа для аналізу стійкості за методом Найквіста – дійсна частина комплексної напруги.

Перетворення Фур'є дає інформацію про частотний склад, але коли виникла та або інша частота в часі і коли вона закінчилась, відповіді на це питання перетворення не дає, але для стаціонарного сигналу це і не потрібно. Для реалізації частотно-часового представлення сигналу необхідне віконцеве перетворення Фур'є або перетворення Вігнера.

Проблеми віконцевих перетворень криються в явищі принципу невизначеності Гейзенберга. Неможливо отримати довільне точне частотно-часове представлення сигналу, тобто неможливо визначити для якогось моменту часу, які спектральні компоненти присутні в сигналі.

Єдине що можна знати так це часові інтервали, за термін яких в сигналі існують полюси частот. Це проблема роздільності. Альтернатива кратно масштабний аналіз. Аналіз на різних частотах і різній роздільній здатності одночасно. Можна отримати хорошу роздільну здатність за часом і погану за частотою на високих частотах і хорошу за частотою та погану за часом на низьких частотах. Цей підхід особливо ефективний коли високочастотні компоненти мають малу тривалість, а низькочастотні – більш протяжні. Такий характер мають більшість сигналів.

Неперервний вейвлет-аналіз виконується аналогічно віконцевому, в тому сенсі що сигнал перемножується з функцією вейвлетом, так само як і з віконцевою функцією при ВПФ и перетворення виконується роздільно для різних ділянок часу сигналу. Однак існують дві відмінності

1. Не виконується ПФ зваженого з вейвлетом сигналу. Тому одиничний пік відповідає синусоїді, тобто негативні частоти не обчислюються.

2. Ширина вікна змінюється, так що перетворення обчислюється для кожної спектральної компоненти.

Слово вейвлет означає маленька хвиля. Під маленькою розуміється те, що ця функція (вікно) має кінчену ширину (компактний носій). Слово хвиля відображає той факт, що вейвлет функція осцилює. Термін материнський означає, що функції з різною шириною носія, породжені одною базовою функцією - материнським вейвлетом. Материнський вейвлет є прототипом всіх віконних функцій.

Перетворення дискретних функцій на кінцевих інтервалах дозволяють досліджувати частотне наповнення сигналів, але не дозволяє визначити, в який момент часу виникає та або інша частота. Тому вони непридатні для аналізу нестаціонарних сигналів, коли потрібна інформація про час появі тієї або іншої частоти.

У випадку, якщо потрібна тимчасова локалізація спектральних компонентів, необхідно звернутися до частотно-тимчасового перетворення сигналу, яке представляють такі перетворення, як віконне перетворення Фур’є (STFT) і вейвлет-перетворення.

При віконному перетворенні Фур’єсигнал ділиться на відрізки («вікна»), в межах яких його можна вважати стаціонарним. Для цього до сигналу застосовується віконна функція Ω, ширина якої повинна бути рівна ширині вікна.

Віконному перетворенні Фур’є має наступний вигляд:

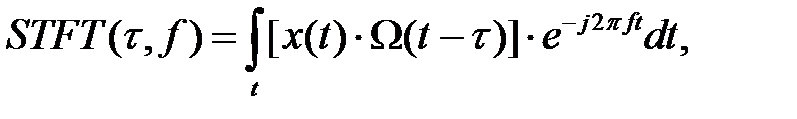(1.33)

де: x(t) – досліджуваний сигнал;

Ω(t) – віконна функція.

Але і STFT має недолік. Межі STFT кореняться в межі невизначеності Гейзенберга, яка указує, що неможливо одержати точне частотно-тимчасове представлення сигналу, тобто не можна визначити для якогось моменту часу які спектральний компоненти присутні в сигналі. Єдине що можна знати це тимчасові інтервали, впродовж яких в сигналі існують смуги частот.

Проблема STFT пов'язана з шириною віконною функцією, що використовується. Чим вужче вікно, тим краще тимчасове уявлення, але гірше частотне. І навпаки. Крім того, чим вужче вікно, тим більше справедливою стає пропозиція про стаціонарність сигналу в межах вікна.

Безперервне вейвлет-перетворення (WT) є скалярним добутком сигналу f(t) і базисної функції:

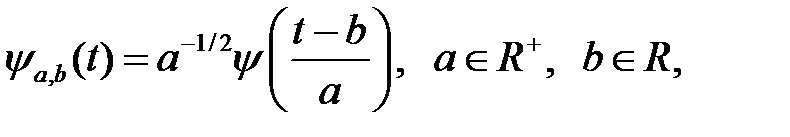
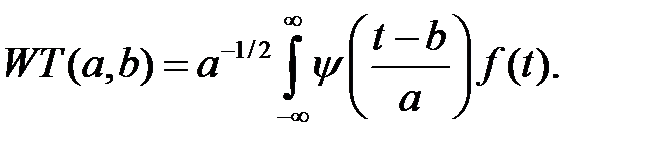(1.34)

Параметр b вказує на розміщення в часі, параметр а – параметр масштабу. Великі значення а відповідають низьким частотам, малі – високим. Операція множення на вікно знаходиться в найближчій функції, яка дозволяє звужувати і розширювати вікно. Звідси з'являється можливість адаптивного до сигналу вибору параметрів вікна.

Базисні функції 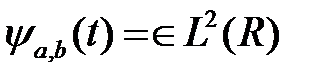є подвійними і коливаються навкруги осі абсцис.

Простір 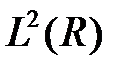є Гильбертовим. В цьому просторі функції повинні бути визначені на всій дійсній осі R (тобто від -∞ до +∞) і повинні мати кінцеву енергію:

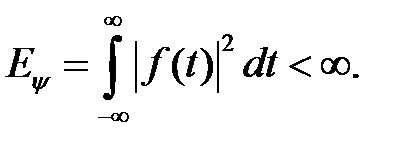(1.35)

Локальне середнє значення кожної функції з повинно прагне нуля на ±∞.

Базисні функції ψ_а,b(t) називається вейвлетом (в перекладі – короткі хвилі) і можуть розглядатися як версії функції ψ(t), що масштабуються і зсунуті.

На рис. 1.5. показано розбиття частотно-часового плану для STFT (а) і для WT (б). Відповідно принципу невизначеності Гейзенберга звуження вікна аналізу по тимчасовій області викликає розширення його в частотній. Таким чином площа вікна залишається постійною, а розподільна здатність по частоті і за часом різна. На низьких частотах якнайкраща частотна розподільна здатність, а на високих – тимчасова.

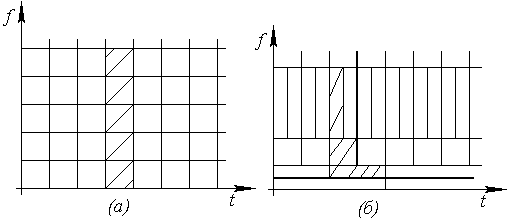
Рис. 1.5. Розбиття частотно-часового плану: а) STFT; б) WT.

Для того, щоб було можливе зворотне отримання сигналу f(t) з результату WT, функція ψ(t) повинна задовольняти умові:

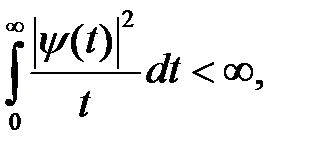(1.36)

де ψ(t) – перетворення Фур’є.

Якщо ψ(t) – локальна функція, то з (1.36) вимагається, щоб її середнє значення дорівнювало нулю:

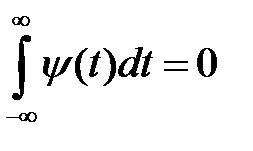(1.37)

Тоді формула реконструкції має вигляд:

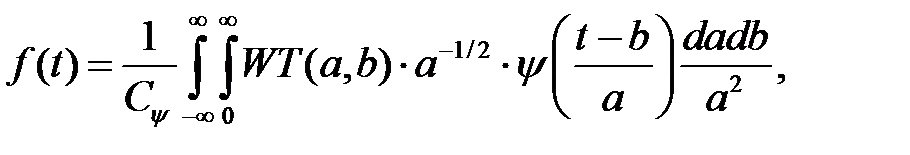(1.38)

де С_ψ – значення виразу (1.26)

Як видно з (1.38), f(t) може бути виражене через суму функцій ψ(t) з терезами WT(а, b).

Дискретизоване вейвлет-перетворення.Параметри а і b в WT змінюються безперервно і тому безліч базисних функцій є надмірною, отже необхідна дискретизація значень а і b при збереженні можливості відновлення сигналу. Дискретизація здійснюється таким чином:

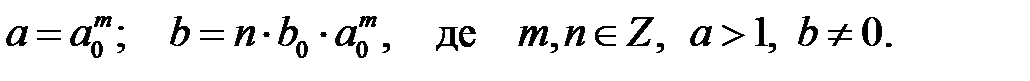(1.39)

Можливий довільний вибір параметра b₀. З (1.39) видно, що параметр місцеположення залежить від параметра масштабу. Із збільшенням масштабу збільшується розмір кроку зсуву.

Для дискретних значень а і b вейвлет функція представляється у вигляді:

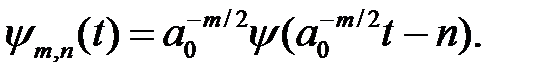(1.40)

Дискретизороване перетворення називаються вейвлет-рядами і визначаються шляхом дискретизації WT:

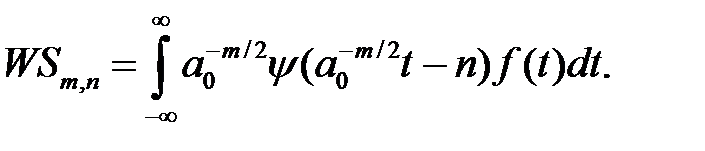(1.41)

Відновлення функції f(t) можливе в тому випадку, якщо існують числа А>0 і B<∞, такі, що:

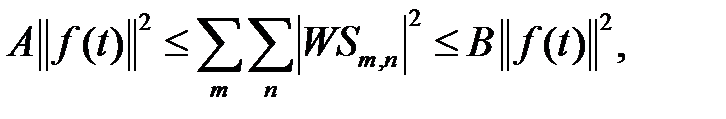(1.42)

для всіх f(t) в L²(R).

Це означає, що хоча реконструкція сигналу f(t) по вейвлет-коефіцієнтах може не співпадати точно з f(t), вона буде близька до нього в середньоквадратичному значенні. Якщо А=В=1 і а₀=2, то можливе повне відновлення і сімейство базисних функцій ψ(t) утворює ортогональний базис. Тоді

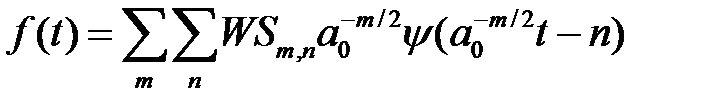. (1.43)

Якщо базисні функції нормалізоване, то С_ψ=1.

Дискретне вейвлет-перетворення (DWT).На практиці WT застосовується до сигналів кінцевої довгі. Таким чином, його необхідно модифікувати, щоб з сигналу деякої довжини одержати послідовність коефіцієнтів тієї ж довжини. Таке перетворення називається дискретним вейвлет-перетворенням (DWT).

Базисні функції f(t) і ψ(t) визначені, що автоматично гарантує кінцівку послідовностей hn і gn. Сигнал, який піддається перетворенню, має довжину N=2^d, d Z⁺.

DWT можна описати в матричному вигляді або шляхом блоків-фільтрів.

1. Нехай вектор v^j – послідовність коефіцієнтів с_j,n для деякого j. Цей вектор перетворюється на вектор v^j+1, що містить послідовність с_j+1,n і d_j+1,n кожна з яких половинної довгі. Перетворення можна записати у вигляді матричного виразу:

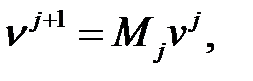(1.44)

де М_j – квадратна матриця, що складається з нулів і елементів hn, помножених на √2. Через властивості h_n матриця, зворотна М_j, є транспонованою.

Як приклад, розглянемо фільтр довгої L=4, послідовність N=8. Послідовність g_n обчислюється з h_n по формулі, де t=L/(2-1)=4/(2-1)=4 Тоді операція матрично-векторного виразу буде представлена у вигляді:

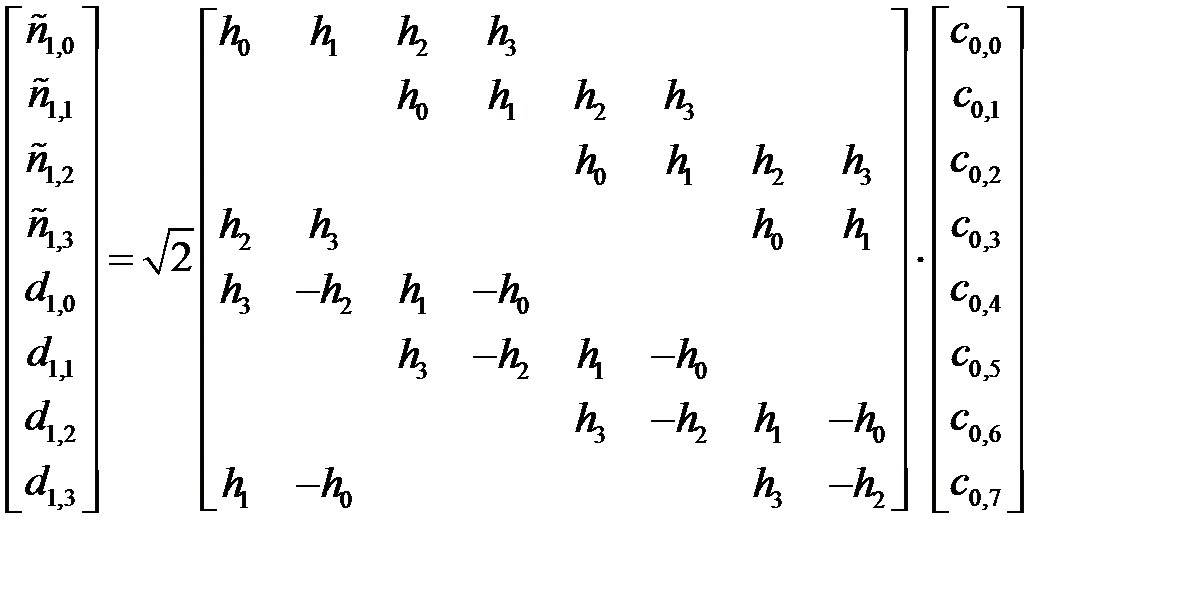(1.45)

Зворотне перетворення полягає в множенні v^j+1 на транспоновану матрицю МjТ:

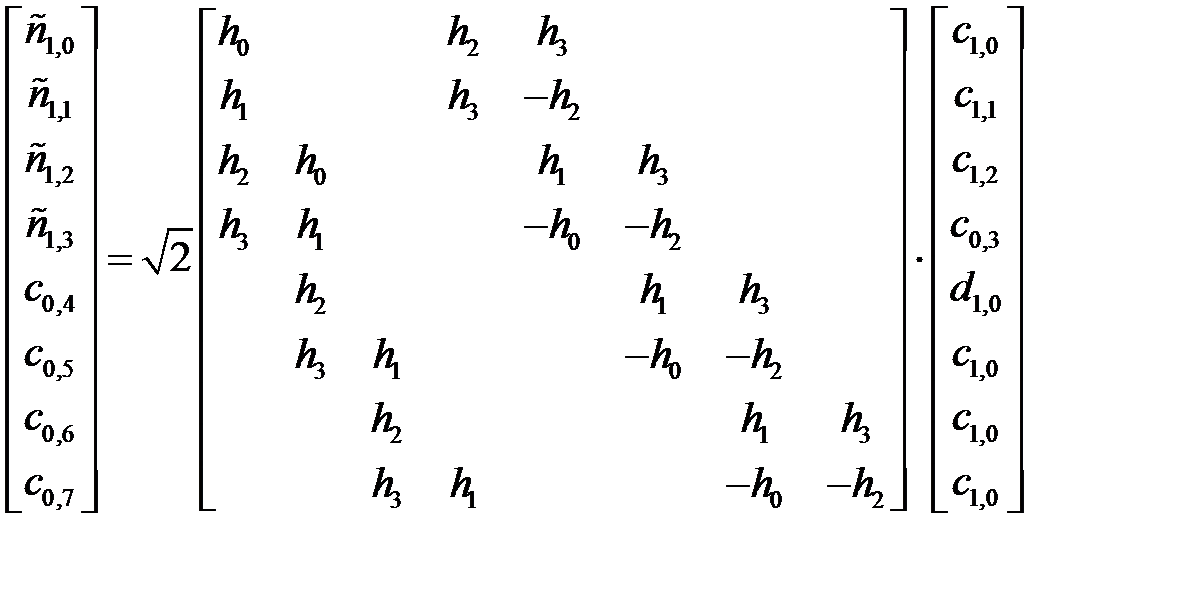(1.46)

Повне DWT полягає в інтерактивному множенні верхньої половини вектора vj+1 на квадратну матрицю Мj+1, розмір якої 2d-j. Процедура може повторюватися d раз, поки довга вектора не стогне дорівнювати 1. В четвертій і восьмій рядках послідовність hn циклічно зсунута: коефіцієнти, що виходять за межі матриці справа, поміщаються в той же рядок зліва. Це означає, що DWT є точно одним періодом довгі N WS сигналу 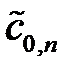, одержувана шляхом нескінченного періодичного продовження 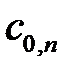. DWT, будучи визначено таким чином, використовує періодичність сигналу.

2. У разі опису DWT шляхом блоків-фільтрів (в даному прикладі) використовується два фільтри g_n і h_n, банк фільтрів є двополюсним і може бути зображений, як показано на рис. 1.6.

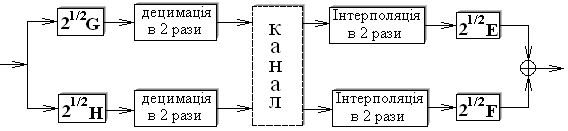
Рис. 1.6. Опис DWT шляхом блоків-фільтрів.

Фільтри F і E означають фільтрацію h_-n і g_-n відповідно. В нижній області схеми виконується низькочастотна фільтрація. В результаті виходить деяка апроксимація сигналу, позбавлена деталей – низькочастотна (НЧ) субсмуга. У верхній частині схеми виділяється високочастотна (ВЧ) субсмуга. Схема, рис. 1.7. ділить сигнал рівня j=0 на два сигнали рівня j=1. Далі вейвлет-перетворення образується шляхом рекурсивного вживання даної схеми до НЧ частини.

Термін зсування використовується в тому сенсі, що він відноситься до місця розташування вікна і вікно рухається вздовж сигналу. Цей термін відноситься до часової інформації, присутньої в результаті перетворення. Однак при ВП ми не маємо частотного параметра, як це було при ВПФ. Замість нього ми маємо параметр масштабу, величину зворотну частоті.

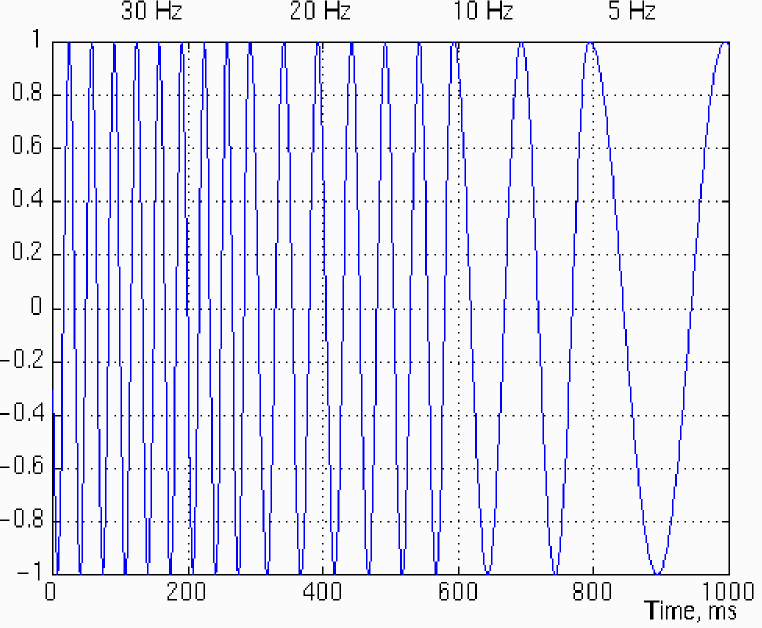
Рис. 1.7. Приклад нестаціонарного сигналу

Параметр масштабу має аналогію з масштабом географічних карт. Великі значення масштабу відповідають малій кількості деталей, глобальному представленню сигналу, малі значення дозволяють розрізняти малі деталі. Аналогічно в термінах частоти, низькі частоти – відповідають глобальній інформації про сигнал (яка утримується на протязі всієї тривалості), а високі частоти – детальній інформації, прихованим можливостям, які мають малу протяжність.

Масштабування як математична операція, розширює або стискує сигнал. Великі значення масштабів відповідають розширенню сигналу, а малі значення стисненим версіям.

Материнський вейвлет – прототип для всіх функцій (вікон), які отримують із нього шляхом стиснення (розширення). Прикладами материнських вейвлетів є вейвлети Морле і Мексиканська шляпа.

На рис. 1.8 приведено нестаціонарний сигнал, який складається з частот 30, 20, 10 і 5 Гц.

На рис. 1.8 показано безперервне вейвлет перетворення (НВП). В якості осей використані зсув і масштаб (а не час і частота). Однак зсув тісно пов'язаний з часом, так як він показує розташування вейвлета за часом. Зсування материнського вейвлета може розглядатись як час який пройшов з початкового терміну часу. Масштаб обернений частоті. Малі масштаби відповідають високим частотам, тому на мал., де масштаби близькі до нуля відповідають високим частотам. Верхняя частота сигналу 30 Гц з'являється на самих малих масштабах при зсувах від 0 до 30. А сама низька 5 Гц з'являється в кінці осі зсувів і на самих великих масштабах.

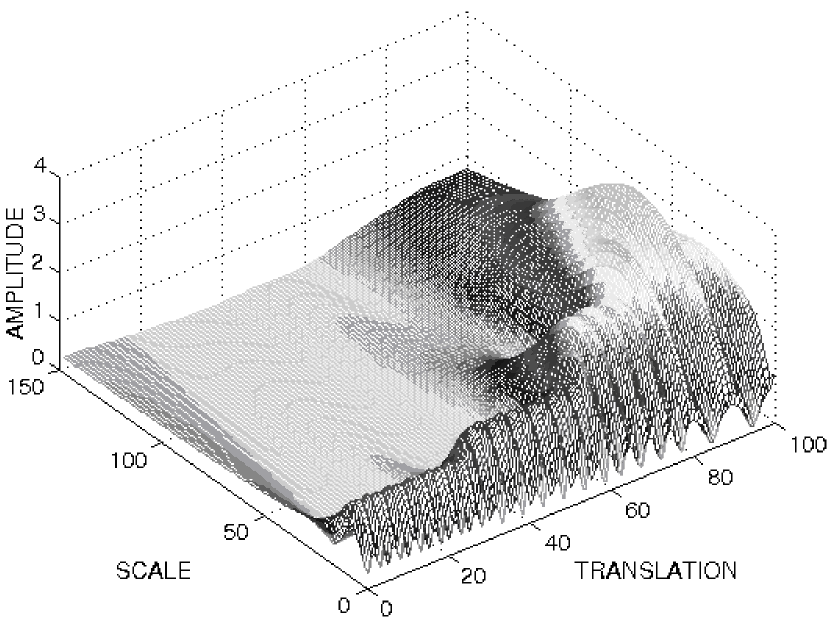
Рис. 1.8. Неперервне вейвлет - перетворення сигналу

Властивості роздільної здатності на відміну від ВПФ яке має фіксовану розмежувальну здатність для всіх проміжків часу і частот, НВП має хорошу розмежувальну здатність за часом і погану за частотою на високих і навпаки для малих частот.

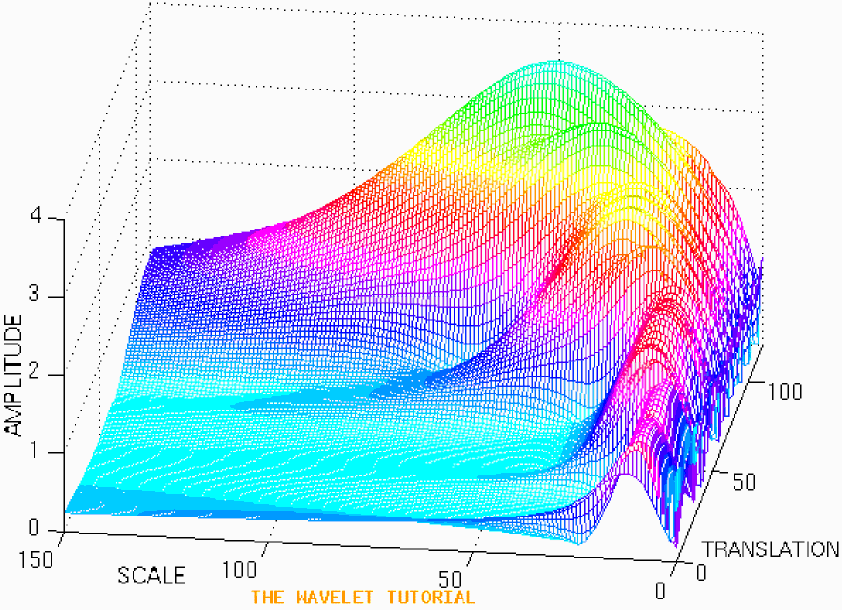
Рис. 1.9. Ілюстрація розмежувальної здатності НВП

На рис. 1.7 показану ту ж площину але під іншим кутом обзору, щоб краще проілюструвати властивості розмежувальної здатності.

На рис 1.8. на високих частотах краще розмежування за масштабом (тобто вузькі, ми можемо точно сказати, який масштаб використано), що відповідає гіршому розмежуванню за частотою. На низьких частотах і більших масштабах ми спостерігаємо зворотну картину. Наведено 100 точок на осі зсувів, що відповідає 1000мс, а 150 точок осі масштабів відповідає полоси частот 40 Гц.

Найпоширенішими є хвильки: Хаара, Стромберга, Габора, Добеші-Жаффара-Журне, Добеші, Гроссмана-Морле, Мексіканський капелюх, Койфмана, Мальвара-Мейера-Койфмана, Шеннона, Коена-Добеші-Фоно, Жеронімо-Хардіна-Масопуста, Беттла-Лемері та інші.

Таблиця 1.2. Приклади найпростіших вейвлет-функцій.

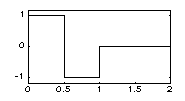
HAAR - вейвлет:
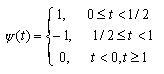
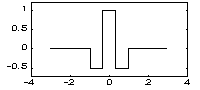
FHAT - вейвлет ("Французький капелюх" - French hat):
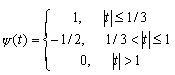
Wave - вейвлет:
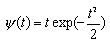
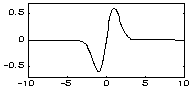
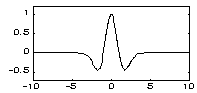
MHAT - вейвлет ("Мексиканський капелюх" - Mexican hat):
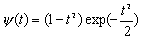
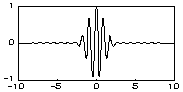
Вейвлет Морле (образує комплексний базис):

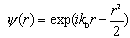
Контрольні запитання

1.Яку функцію називають автокорреляційною?

2.Якою може бути мінімальна частота дискретизації сигналу для виключення втрат інформації при використовуванні швидких перетворень Фур’є?

3.Аналоговий сигнал з максимальною частотою в спектрі fmax переведений в дискретну форму з рівномірним кроком дискретизації Dt=1/(2fmax). Чи можлива точна апроксимація аналогової форми сигналу з його дискретних відліків?

4.Як розрахувати спектр дискретного періодичного сигналу?

5.Що являє собою задача апроксимації?

6.Математична модель системи. Для чого вона призначена?

7.Що таке детермінована, безперервна, лінійна, стаціонарна система?

8.Кореляція між сигналом і перешкодою.

9.Що таке автокороеляційна функція?

10.Призначення вейвлет перетворення. В яких випадках його доцільно виконувати?