Спектральний аналіз

Спектральний аналіз (пряме перетворення Фур'є) використовується для розкладання кривої перехідного процесу F(t), отриманої при моделюванні в області часу, на гармонійні складові. Спочатку обчислюються значення кривої перехідного процесу для значень:

,

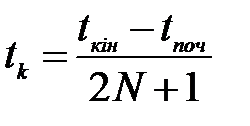де t_поч, t_кін – початок і кінець часового інтервалу перетворень;

N – ціле число, задається користувачем;

k – 1, 2,…, 2N...

Потім за допомогою простого рекурентного методу пряма спочатку апроксимується сумою гармонік:

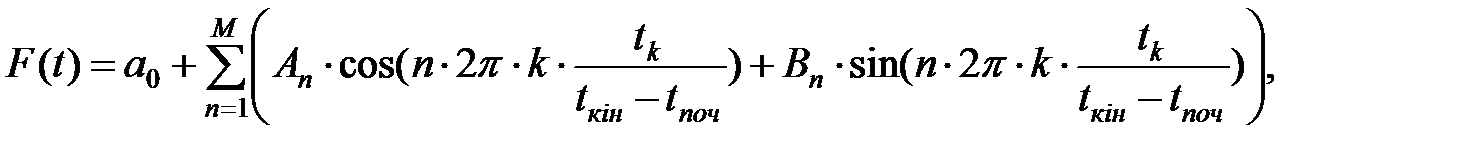
де М – максимальний порядок апроксимуючих гармонік.

Потім перераховуються до виду:

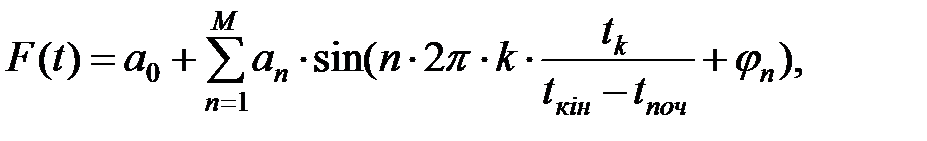
де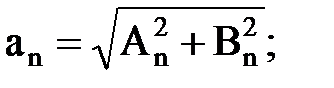

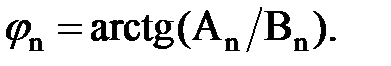
Результати перетворення видаються на друкування у виді таблиці залежності a_n і φ_n від номера апроксимуючої гармоніки.

Спектральний аналіз виконується після розрахунку перехідних характеристик швидким перетворенням Фур’є із розрахунком коефіцієнта нелінійних спотворень. Можна розраховувати частотні характеристики пристроїв, заданих передаточною функцією, але перетворення Лапласа не можна використовувати для завдання лінійних блоків із постійними коефіцієнтами передачі. Для розрахунку імпульсної характеристики за допомогою перетворення Фур’є в режимі аналізу АС по вісі х задається час, а для побудови годографа для аналізу стійкості за методом Найквіста – дійсна частина комплексної напруги.

Вигляд полінома знаменника спектральної щільності визначається його коренями. При наявності уявних коренів, коли дійсна частина дорівнює нулю, поліном має вид (табл. 1.1):

.

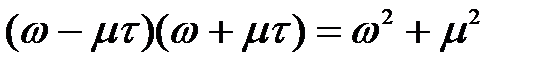В указаному випадку ступінь регулярності процесу дорівнює нулю. Якщо мається чотири комплексних корені, які описуються двома параметрами - резонансною частотою та параметром затухання випадкового процесу, то поліном дорівнює:

.

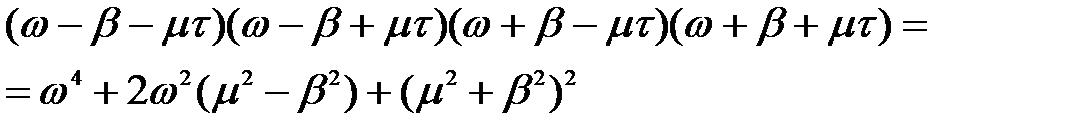Поліном четвертого степеня, який містить тільки парні степені, має чотири кореня, два з яких. являються комплексно-спряженими. Ступінь регулярності може змінюватись від нуля до нескінченності і залежить від відношення резонансної частоти та параметра затухання випадкового процесу.

Таблиця 1.1. Спектральні щільності найпростіших стохастичних сигналів

№	Назви процесів	Нормовані моделі	Пара-метри
автокореляційних функцій	спектральних щільностей
	Білий шум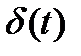
	Випадковий без періодичної складової	е-mt		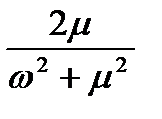m
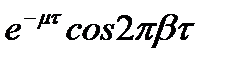
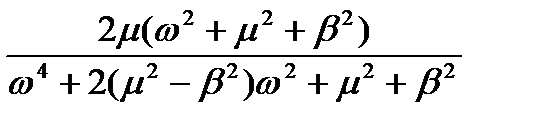
	Випадковий з однією періодич-ною складовою; (функція не має першої похідної)			m b(y)
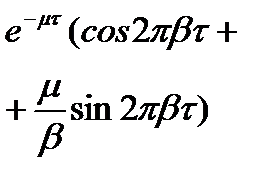
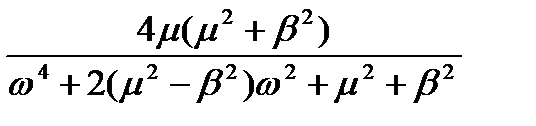
	Випадковий з періодичною складовою; (функція диференційовна)			m b(y)
	Періодичний		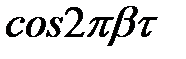d(w-b)	b

В табл. 1.1 приведені параметри автокореляційних функцій та спектральних щільностей випадкових процесів. Природно, тільки добуток приведених поліномів забезпечить парність полінома знаменника спектральної щільності. Поліном являється узагальненим, так як при y = 0 з нього виходить, що w⁴+2m²w²=(w²+m²)².

При m=0 вираз для автокореляційної функції процесу, що вивчається, з періодичною складовою для недиференційованого та диференційованого процесів дорівнює

,

де: D – дисперсія процесу;

t – час.

Більшість стаціонарних випадкових процесів володіє ергодичним властивістю. Суть його полягає в тому, що по одній достатньо довгої реалізації процесу можна судити про всі його статистичні властивості так само, як по будь-якій кількості реалізацій. Іншими словами, закон розподілу випадкових величин в такому процесі може бути одним і тим же як по перетину для ансамблю реалізацій, так і по координаті розвитку. Такі процеси одержали назву ергодичних (ergodic). Для ергодичних процесів має місце:

mx(t) = M{x(t)} = 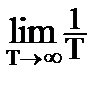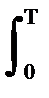x(t) dt = 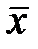, (1.22)

Dx(t) = 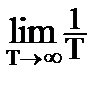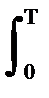(x(t) - mx(t))2 dt = 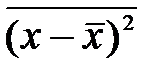= 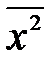- 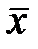², (1.23)

Rx(t) = M{x(t)x(t+t)} = 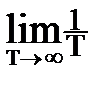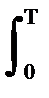x(t)x(t+t) dt. (1.24)

де mx(t) – математичне очікування ергодичного випадкового процесу;

Dx(t) – дисперсія при Т Þ ¥;

Rx(t) – автокорелляційна функція

Властивості ергодичності можуть виявлятися тільки по відношенню до двох перших моментів випадкового процесу, що цілком достатнє для використовування відповідних методик дослідження процесів. Практична перевірка ергодичності процесу звичайно проводиться перевіркою виконання умови Слуцкого:

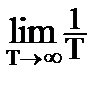
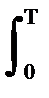K(t) dt = 0. (1.25)

Якщо коваріаціона функція процесу прагне нуля при зростанні значення аргументу (t), то процес відноситься до числа ергодичних, принаймні, щодо моментів першого і другого порядків.

Приклад. Випадкова функція задана виразом Z(t)=X(t)+Y, де X(t) – стаціонарна ергодична функція, Y- випадкова величина, некорельована з X(t). Чи ергодична функція Z(t)?

mz(t)= mz(x)+my, Kz(t)= Kx(t)+Dy. Функція Z(t) стаціонарна, але не ергодична, оскільки при t Þ ¥ має місце Kz(t) Þ Dy.