Механізми виникнення випадкових корисних сигналів
Механізм виникнення стохастичних сигналів у системах нижнього рівня керування АСУ ТП такий: існує два класи сигналів детерміновані на одному полюсі і стохастичні на другому. Стохастичні сигнали можна віднести до класу корисних або сигналів перешкод. Корисний сигнал допускає вимір реалізації й обчислення його параметрів. Але навіть вимірюваний сигнал може вважатися перешкодою, якщо не можна визначити його параметри. Це не завжди залежить тільки від сигналу. Безупинні сигнали виміряються дискретно. Наприклад, якщо інтервал вибірки дуже великий, то можна втратити інформацію про параметри стохастичного сигналу і він перетворюється в чисто випадковий сигнал-перешкоду. Таким чином, від тривалості інтервалу виміру залежить те, наскільки вдало зважується задача про виявлення особливостей стохастичного сигналу.
Механізм виникнення стохастичних сигналів можна представити таким чином. Найбільш розповсюдженим чисто випадковим сигналом є перешкода, наприклад білий шум – (дельта-імпульс) у виді миттєвого спалаху, процесів умикання - вимикання, переключення схем і пристроїв. Коли такий чисто випадковий сигнал надходить на вхід конкретної схеми або пристрою з зосередженими параметрами, то на виході він трансформується в іншій - стохастичний сигнал з визначеними детермінованими властивостями, що залежать від постійних параметрів схеми або пристрою. Наприклад, якщо на вхід інерційної ланки першого порядку надходить випадковий сигнал у виді перешкоди - білого шуму, то сигнал на виході являє собою випадковий сигнал без періодичної складової, параметр загасання якого обернено пропорційний постійній часу інерційної ланки. Таким чином, перешкода трансформувалася в стохастичний сигнал. Такий сигнал складається із сигналом, що характеризує технологічний процес.
Якщо перешкода надходить на вхід ланки другого порядку, де маються два «резервуари» для накопичення енергії, то вихідний випадковий сигнал має резонансну періодичну складову. Дві характеристики стохастичного сигналу визначаються не тільки рівнем перешкоди, але і, головне, параметрами динамічної ланки. Якщо такий сигнал знову надійде на вхід ланки визначеного порядку, то порядок полінома вихідного сигналу відповідно підвищиться. При апроксимації виникає суперечлива задача. З однієї сторони для підвищення точності математичної моделі сигналу порядок полінома апроксимації треба збільшувати, виявляючи особливості стохастичного сигналу. Але з іншої сторони треба враховувати, що сигнал усе-таки випадковий, а збільшення порядку полінома значно збільшує складність рішення задачі, тому бажано порядок полінома понизити. Потрібно вибрати «розумний» порядок полінома.
Має значення інтервал дискретності вимірів стохастичного сигналу. Якщо інтервал часу вимірів обраний таким, що процес практично не змінюється, то автокореляційна функція залишається практично незмінної. Наприклад, у процесі доменної плавки зміни технологічного процесу протягом секунд не приводять до відчутних результатів. Тому інтервал виміру вибирається в десятках хвилин. Однак у процесі прокатки інтервал вимірів може складати десяті частки секунди. Якщо інтервал обраний великим, то можна не устежити за можливими змінами, і автокореляційна функція буде білим шумом, коли взаємозв'язок між суміжними перетинами відсутній.
Для обґрунтування раціонального порядку диференційних рівнянь, які описують завадостійкі системи керування, необхідно проаналізувати динамічні властивості електронних систем. Найбільш простою моделлю елементарної динамічної системи є інерційна ланка накопичення електромагнітної енергії. В таблиці 2.1 приведені приклади проходження найпростішого випадкового сигналу - білого шуму через указані канали. Так випадковий процес у вигляді білого шуму, що проходить через інерційну систему першого порядку, приводить до виникнення випадкового процесу без періодичної складової з параметром затухання, який визначається постійною часу системи. Якщо указаний процес знову поступає на вхід динамічної системи першого порядку, то на виході виникає комбінація (добуток) випадкових процесів без періодичної складової.
Випадковий сигнал з періодичною складовою міг би виникнути на виході коливальної ланки при проходженні через неї білого шуму проте розглянуті об'єкти не описуються диференційними рівняннями другого порядку.
Як показано раніше, частотний склад зміни розмірів має декілька складових, обумовлених різними технологічними факторами. Накладення випадкової складової без періодичної складової з указаною періодичною приводить до появи випадкових сигналів, які містять періодичну складову. Проходження такого сигналу через без інерційну ланку не змінює її властивостей, впливаючи лише на величину дисперсії.
Тому випадкові процеси адекватно описуються моделями диференційованої та недиференційованої функцій. Мінімальний порядок поліному спектральної щільності дорівнює чотирьом. Основною характеристикою випадкового процесу служить відношення резонансної частоти b до параметру затухання m випадкового процесу, яке називається ступенем регулярності y випадкового процесу.
Таблиця 2.1. Проходження випадкових сигналів через найпростіші електронні системи
| Вхід | Електронна система | Вихід | |
| № | Спектральна щільність | Диферен-ційне рівняння | Спектральна щільність |
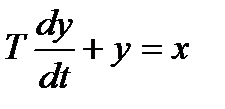
| 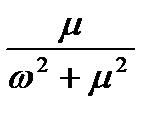
| ||
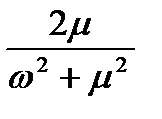
| 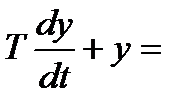
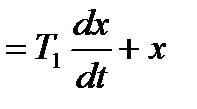
| 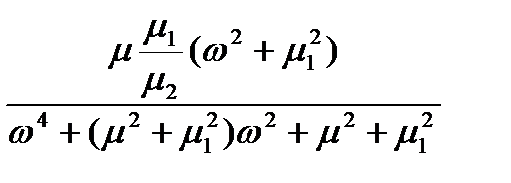
| |
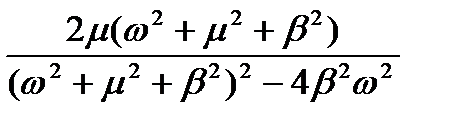
| 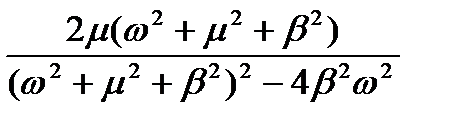
| ||
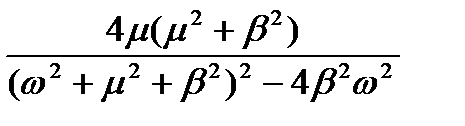
| 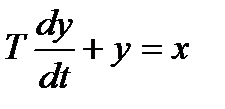
| 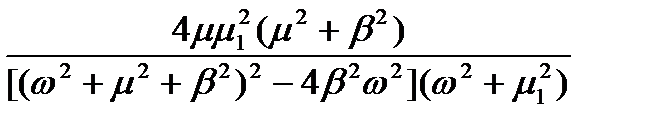
| |
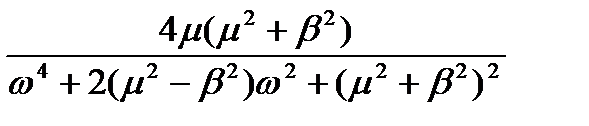
| 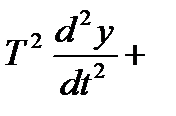
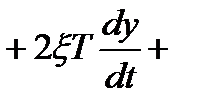
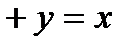
| 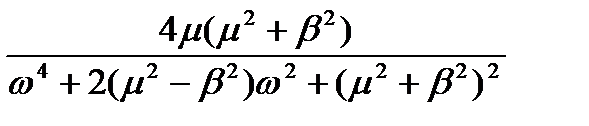 *
* *
* 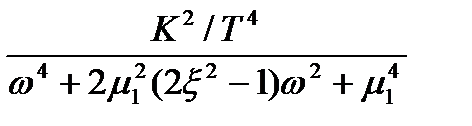
|
Таким чином, апроксимація спектральної щільності поліномом четвертого порядку дозволяє дослідити важливе сполучення двох параметрів автокореляційної функції випадкового процесу: резонансної частоти процесу та параметра затухання кореляційної залежності, що неможливо виконати при апроксимації поліномом другого ступеня.
Таблиця 2.2. Еквівалентні смуги пропускання системами білого шуму
| Передатні функції електронних систем | Еквівалентні параметри | |||
| Розімкнених | Замкнених | Смуга пропускання, Гц | Постійна часу, с | |
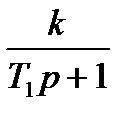
| 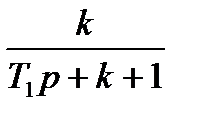
| 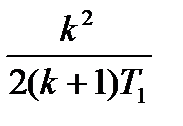
| 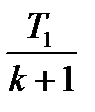
|
Дата добавления: 2015-03-03; просмотров: 1000;
