Двовимірна оцінка похибок апроксимації
Задача апроксимації – представлення довільних складних функцій f(x) простими і зручними для практичного використовування функціями j(x) так, щоб відхилення j(x) від f(x) в області її завдання було якнайменшим по певному критерію наближення. Функції j(x) одержали назву функцій апроксимації.
У більшості практичних випадків аналітичний вид функцій сигналів досліджуваних процесів відразу невідомий, тому одержують безліч значень функцій xn у фіксовані моменти часу nDt, n = 0, 1, 2, …, N-1, N – довжина реалізації. Для наступних розрахунків зручно перетворити послідовність xn у нову послідовність un, що має нульове вибіркове значення: 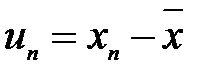 , де
, де 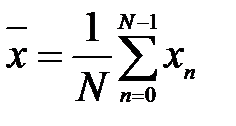 . У випадку стаціонарного ергодичного процесу
. У випадку стаціонарного ергодичного процесу 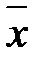 являє собою незміщену оцінку середнього значення.
являє собою незміщену оцінку середнього значення.
При прямому способі обчислення АКФ її оцінка для реалізації un, що належить стаціонарному процесу і має середньому значенню 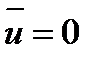 , при затримці за часом rDt обчислюється по тимчасовому ряді un за такою формулою:
, при затримці за часом rDt обчислюється по тимчасовому ряді un за такою формулою:
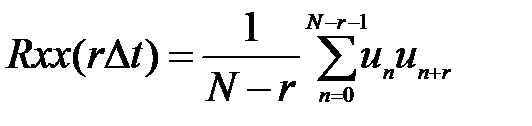 ,
,
r = 0, 1, 2, ... , m, де r називається зрушенням, а m – максимальним зрушенням (m<N). Якщо розділити значення такий АКФ на дисперсію сигналу, то одержимо дискретні значення нормованої АКФ.
Всі обчислення виконували на ПК PENTIUM II 450 Мгц під керуванням ОС WINDOWS 98 SE у середовищі математичного моделювання MathCAD 2000 Professional.
При апроксимації підрахованих значень АКФ функціями (1.15) чи (1.16) функція b буде залежати тільки від одного аргументу y. Найбільше наочно таке рішення представляється у виді графіка, по осі ординат якого відкладене значення b, а по осі абсцис – значення параметра (для функцій (1.5) і (1.8)). Для функцій (1.6) і (1.7) R(r(t)) у (1.20) визначається двома параметрами (параметром загасання і резонансною частотою), тому необхідно побудувати тривимірний графік. У цьому випадку зручно по вертикальній осі відкласти величину, зворотну (1.20), тоді шуканому мінімуму буде відповідати вершина тривимірного графіка.
Для побудови графіка необхідно задатися діапазоном зміни параметрів і кроком їхньої зміни. Границі зміни параметрів b і m можна визначити по декількох найбільш характерних крапках кривої R(t). Діапазон зміни b можна оцінити по тривалості періоду (b = –p/Tb), а діапазон зміни параметра m можна оцінити так: m = 1/Тm, де Тm – крапка на осі абсцис, що перетинає дотична, проведена до експоненти е-mt (експонента в цьому випадку «проходить» по вершинах загасаючої косинусоїди). Крок зміни параметрів b і m обмежується ресурсами застосовуваного ПК.
| ,рад/с |
| б) |


| , рад/с |
| , Гц |

| , рад/с |
| а) |


| , рад/с |
| , Гц |

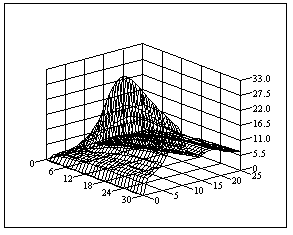
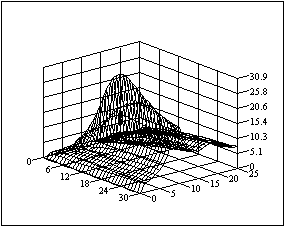
Рис. 1.2. – Вплив параметра загасання і резонансної частоти апроксимуючої функції при ступені регулярності сигналу 5 на оцінку помилки: а) диференційної; б) не диференційної.
Запропоновано ітераційний алгоритм пошуку: спочатку задаємося досить великим діапазоном зміни b і m з великим кроком квантування, відшукуємо максимум, далі звужуємо діапазони і, відповідно, кроки зміни b і m і так далі доти, поки Db >2Eb і Dm >2Em , де Db і Dm – кроки зміни b і m, а Еb і Еm – необхідна точність обчислення оптимальних параметрів. Варто помітити, що верхню границю зміни параметра b варто вибирати до значення p/Dt, де Dt – час дискретизації досліджуваного стохастичного сигналу.
Дослідження провели для двох характерних випадкових сигналів з візуально помітним ступенем регулярності. За допомогою персонального компьютера побудували оцінки автокореляційних функцій.
На рисунку 1.2. представлені графіки зміни величин, зворотних від параметрів b і m при апроксимації АКФ сигналу диференційної (рис. 1.2. а)) і не диференційної (рис. 1.2. б)) функціями. В обох випадках значення параметрів вийшли однаковими b = 0,90 рад/c і m = 0,14 Гц. Обчислення вироблялися з точністю 0,05 рад/c і 0,005 Гц відповідно.

| Rd (m, b, t) |
| Rn (m, b, t) |
Рис. 1.3. - Вид аналітичних оптимальних апроксимацій експериментальних оцінок автокореляційних функцій випадкового
сигналу зі ступенем регулярності одиниця.
Якщо на періодичний (детермінований) сигнал накладається шум, то його ступінь регулярності, як правило, зменшується. Проведено дослідження випадкового сигналу зі ступенем регулярності менше одиниці, по формулі 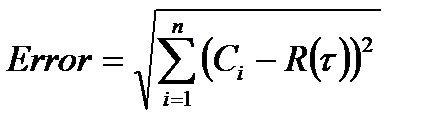 (де Сі – значення вхідного сигналу), оцінені помилки апроксимації. На рисунку 1.4. представлені оцінки помилок апроксимацій.
(де Сі – значення вхідного сигналу), оцінені помилки апроксимації. На рисунку 1.4. представлені оцінки помилок апроксимацій.
| а) |


| , рад/с |
| , Гц |



| , рад/с |
| , Гц |

| б) |
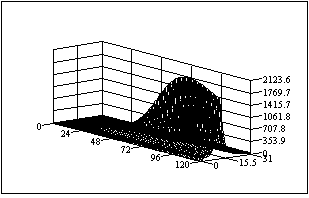
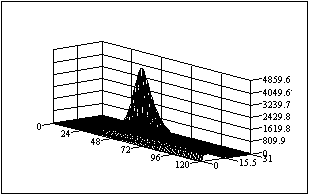
Рис. 1.4. – Вплив параметрів аналітичних апроксимуючих
функцій на величину помилки для ступеня регулярності
процесу менше одиниці: а) диференційної;
б) не диференційної апроксимацій.
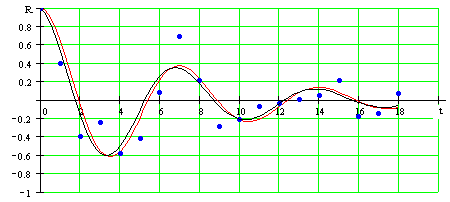
У цьому випадку для диференційної функції параметр резонансної частоти складає 1,1 рад/с, параметр загасання 0,95 Гц, а для не диференційної функції ці параметри відповідно рівні 0,7 рад/с і 0,63 Гц. Незважаючи на великі розходження абсолютних значень резонансних частот і параметрів загасання для диференційної і не диференційної функції ступеня регулярності останніх розрізняються мало: для першої Y = 0,184, а для другої Y = 0,177. Графіки автокореляційних функцій показані на рисунку 1.5.
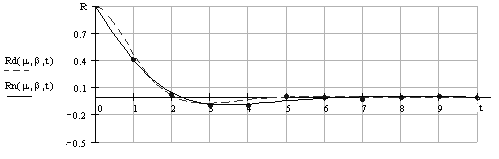
Рис. 1.5. – Оптимальні моделі автокореляційних функцій стохастичного сигналу зі ступенем регулярності в частки одиниці.
Аналіз сигналів, що мають періодичний загасаючий характер, показує, що апроксимація АКФ, де відносини y = 1/2ln[R(t)]-1 – ступінь регулярності яких одиниця і більш (рис. 1.1.), приводить до однакових відхилень (помилкам апроксимації). Коли ж ступінь регулярності процесу складає частки одиниці (тобто швидко загасаюча АКФ), помилки апроксимацій функціями можуть відрізнятися. Так, наприклад, з малюнка 3 видно, що при апроксимації не диференційної функцією помилка зменшується майже в два рази в порівнянні з дифференцируємою функцією.
Таким чином, при апроксимації експериментальних оцінок автокореляційних функцій технологічних процесів аналітичними функціями помилка апроксимації носить екстремальний характер. Зі збільшенням ступеня регулярності випадкового процесу область мінімальних помилок більш розмиті і не диференційної і диференційної функції приводять приблизно до однакових помилок, хоча невелика перевага варто віддати диференційної функціям. Зі зменшенням ступеня регулярності сигналу для не диференційної функції помилка менше, ніж для диференційної. Припустима область оптимальних значень істотно менше, що вимагає застосування адаптивних методів пошуку екстремуму.
Результати досліджень застосовувалися для стохастичного синтезу структури і параметрів завадостійких систем керування технологічними процесами поперечно-клинової прокатки і накатки профілів складної форми: швидкості виправлення прутка з бунта дроту, довжини прутка, що відрізається, з бунта дроту, подачі прутка зменшуваної маси на задану відстань у циклічно з'являється зазор між безупинно обертовими валками, положення супорта напівавтомата для накатки профілів, частоти обертання прокатних валків, діаметра і довжини деталі, що прокочується, в агрегатно-модульних комплексах лінійного і радіального типів.
Дата добавления: 2015-03-03; просмотров: 1338;
