Моделі автокореляційних функцій стаціонарних сигналів

Електронні системи мають змінні: вхідні та вихідні, впливи: збурюючі та керуючі. Незважаючи на детерміновану природу більшості з них, у реальних умовах функціонування їх варто розглядати переважно як стохастичні, що збільшується дією перешкод. Тому для їхнього опису застосовуються методи математичної статистики. Найбільше поширення одержала теорія стаціонарних випадкових сигналів.

Основною характеристикою випадкового сигналу є автокорреляційна функція (АКФ), що показує зміну тісноти зв'язку між двома перетинами сигналу з часом. Якщо процес ергодичний і його реалізація описується відомою функцією часу x(t), то АКФ має вид:

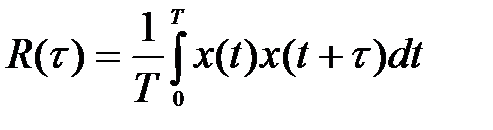(1.12)

Після визначення достатнього числа ординат функції R(t) звичайно виникає задача апроксимації АКФ простим аналітичним вираженням, зручним при подальших дослідженнях і які мають чіткий фізичний зміст. Причому аналітичне вираження повинне відповідати загальним властивостям кореляційних функцій і відображати характерні властивості досліджуваного стохастичного сигналу. Одержала поширення апроксимація R(t)вираженнями виду:

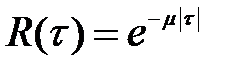; (1.13)

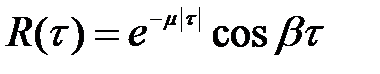; (1.14)

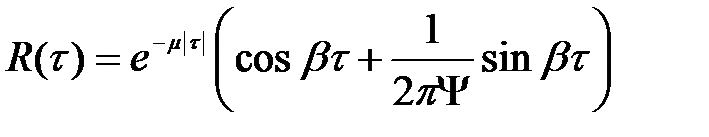; (1.15)

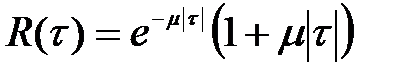, (1.16)

де m – параметр загасання випадкового сигналу, Гц;

b – резонансна частота, Гц;

Y – ступінь регулярності, Y=b/m .

Параметр загасання показує міру взаємозв'язку між суміжними перетинами сигналу, тобто як би "міру стохастичності", де для перешкоди ці значення дуже великі, а для сигналу, що наближається до детерминированному, – малі. Резонансна частота визначає основну гармонійну складову.

Перші дві моделі відповідають недифференційовному сигналу, а останні два – дифференційовному, тобто сигнали, що має першу похідну, що спрощує обчислення його швидкості; а друга і третя моделі відповідають випадковому сигналу з періодичною складовою.

З виражень (1.12 – 1.15) видно, що АКФ буде визначатися одним (у випадку (1.12) і (1.16)) чи двома ((1.13), (1.14)) параметрами. Ясно, що підібрати ці параметри так, щоб апроксимуюча функція «проходила» через усі підраховані ординати АКФ, неможливо. Тому параметри b і m необхідно визначити відповідно до деякого критерію. У якості такого будемо використовувати мінімум математичного чекання квадрата відхилень дискретних значень R_xx(rDt,m,b) від апроксимуючої аналітичної функції R(t,m,b): M(R_xx(rDt,m,b)-R(rDt,m,b)), τ=rΔt, r=0…m. Іншими словами математичне чекання є функцією двох аргументів (для функцій (1.13), (1.14)) і завдання полягає в пошуку мінімуму функції:

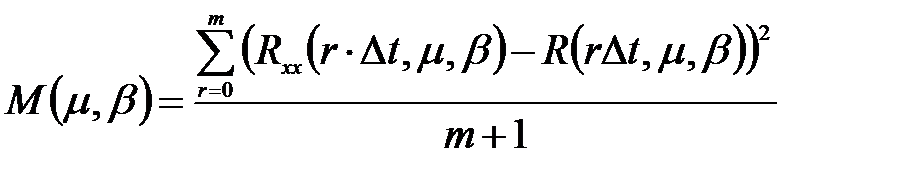. (1.17)

Вхідні та вихідні випадкові процеси нормалізовані, тому дисперсія одинична. Дисперсія випадкового процесу на виході зв'язана із вхідною через квадрат коефіцієнта передачі системи керування, отже

D_вих = K₂D_вх.

Білий шум, проходячи через ланку першого порядку перетворюється у випадковий процес без періодичної складової, де параметр затухання зворотний постійній часу ланки. Випадковий процес без періодичної складової, проходячи через ланку першого порядку. перетворюється в спектральну щільність з поліномом четвертого порядку з дійсними коренями, а якщо вказана ланка форсована, то в чисельнику спектральної щільності з'являється поліном другого ступеня.

Випадковий недиференційний процес, проходячи через підсилювальну ланку, не змінює своєї спектральної щільності. Проходження такого процесу через ланки пертого і другого порядку приводить до поліномів спектральної щільності шостого і восьмого порядків.

На практиці намагаються використовувати якомога менший порядок полінома спектральної щільності сигналу з врахуванням особливостей процесу.

Розглянемо випадковий процес, апроксимований нормованою функцією:

,

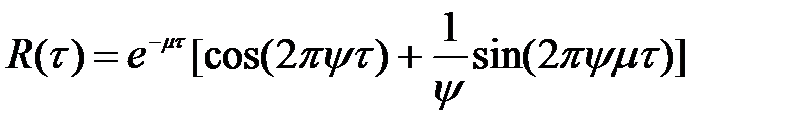де m – параметр затухання;

y – ступінь регулярності;

t – час.

Знайдемо час, коли функція досягає першого мінімуму:

.

.

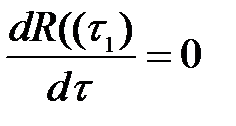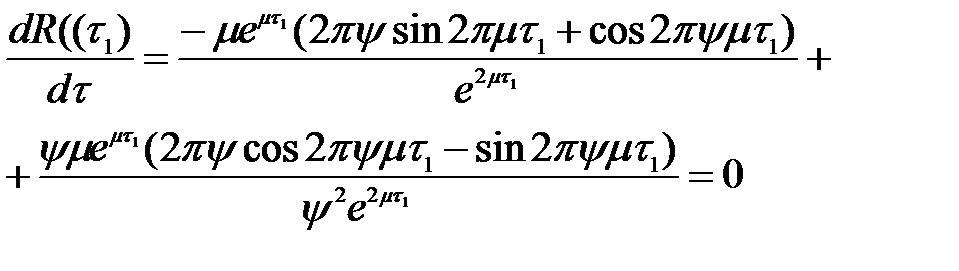Після перетворень одержали:

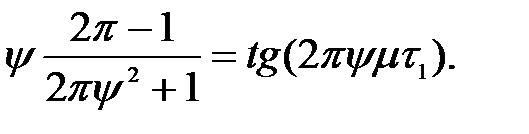
Звідки:

.

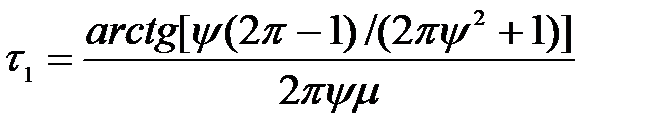Таким чином, час мінімуму автокореляційної функції залежить від ступеня регулярності випадкового процесу та параметру m. Якщо 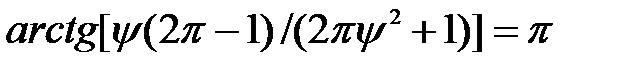, то резонансна частота процесу дорівнює 2t₁.

Проаналізуємо екстремальну функцію:

.

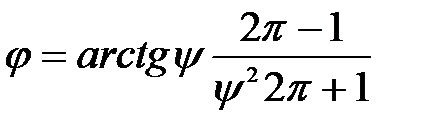Знайдемо екстремум із умови: 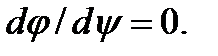(1.18)

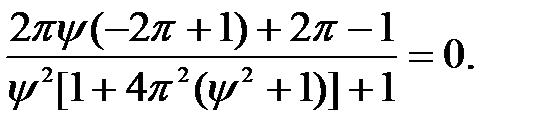
Рівність нулю чисельника можлива, коли y=0,4.

Автокореляційна функція в іншому вигляді:

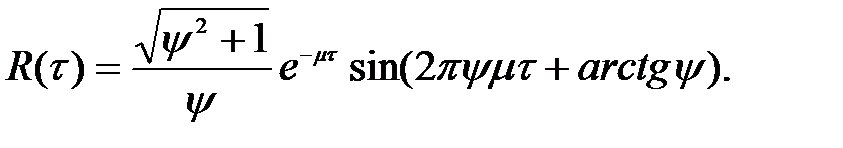(1.19)

Взаємозв'язок ординати мінімуму автокореляційної функції і ступеня регулярності має вигляд:

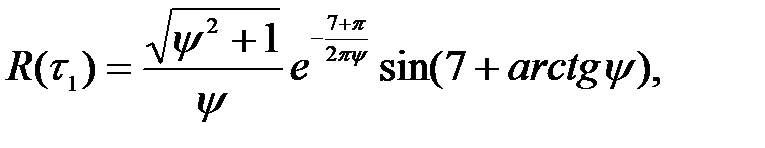(1.20)

де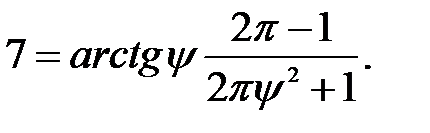

Якщо 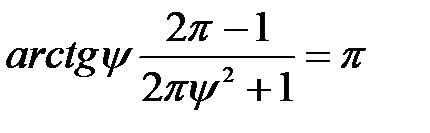, то вираз спрощується: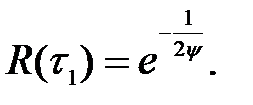

В цьому разі ступінь регулярності дорівнює:

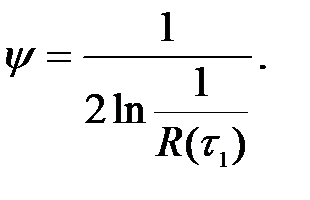(1.21)

Таким чином, використання простої формули для оцінки ступеня регулярності випадкового процесу по ординаті першого мінімуму автокореляційної функції можливо лише поза межами діапазону 0,05<R(t₁)<0,91. коли максимальна помилка оцінки ступеня регулярності не перевищує 0,05. В інших випадках треба використовувати більш складну функцію.

На рисунку 1.1 приведені залежності ступеня регулярнояті випадкового процесу від ординати першого мінімуму автокореляційної функції, одержані по точній і простій формулах. Якщо ордината змінюється від 0,1 до 0,4, то ступінь регулярності – відповідно від 0,017 до 0,495, а якщо ордината в межах 0,78 – 0,95, то ступінь регулярності відповідно 2 – 100. При ординаті, рівній 0,75, ступінь регулярності одинична.

Із формули для визначення часу досягнення автокореляційною функцією першого мінімуму знайшли резонансну частоту в вигляді:

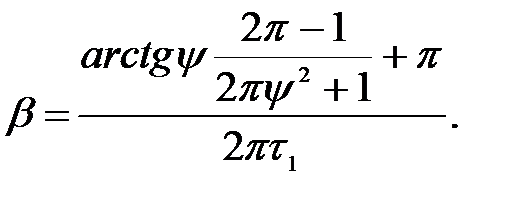
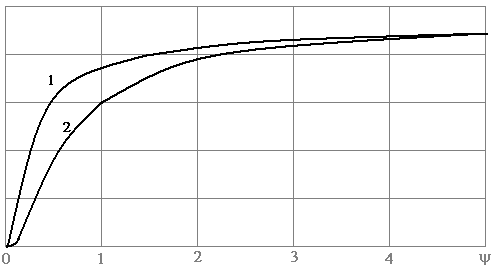
Рис. 1.1. Залежності ступеня регулярності дифференційованого випадкового процесу від ординати першого мінімуму

автокореляційної функції: 1 – точний розрахунок за (1.20),

2 – наближений розрахунок за (1.21).

При дуже малих значеннях ступеня регулярності y < 0,01 та дуже великих y >100 чисельник дорівнює p, і час першої половини періоду автокореляційної функції зворотно пропорційний подвоєній частоті. В іншому разі одержану оцінку в залежності від ступеня регулярності треба перемножити на коефіцієнт, який знаходиться в межах від одиниці до 1,35. Максимальне значення коефіцієнту при ступені регулярності 0,4 дорівнює близько 1,35.

Таким чином, ордината першого мінімуму автокореляційної функції випадкового процесу дозволяє оцінити ступінь регулярності випадкового процесу, а час досягнення мінімуму достатній для оцінки резонансної частоти випадкового процесу, відношення останнього до першого дозволяє визначити параметр затухання.

Якщо використати апроксимацію автокореляційної функції випадкового процесу недиференційованою функцією, то використання такої методики неможливе, оскільки не можна знайти похідну (вона не існує). Але як метод приблизної оцінки його можна застосувати і в цьому випадку.

Визначивши постійні параметри автокореляційної функції, побудували її графік в залежності від часу.

Таким чином, для обчислення ступеня регулярності диференційованої функції випадкового процесу достатньо визначити ординату першого мінімуму автокореляційної функції, а для визначення резонансної частоти або параметру затухання необхідно оцінити час досягнення першого мінімуму.