Актуальность технического обслуживания 14 страница

В-третьих, факторный анализ применяется при проверке пси­хометрических свойств опросников, особенно когда они исполь­зуются в новых культурах или популяциях. Например, предполо­жим, что, в соответствии с руководством по использованию авст­ралийского личностного теста, его следует обрабатывать путем сложения баллов, полученных по всем нечетным заданиям, кото­рые формируют одну шкалу, в то время как сумма баллов, полу­ченных по всем четным заданиям, образует другую шкалу. Когда этот тест предъявляется выборке людей в Великобритании и вы­числяются корреляции между заданиями и затем факторизуются, то должно быть обнаружено два фактора, причем один фактор

должен иметь существенные нагрузки по всем нечетным задани­ям, а другой фактор — существенные нагрузки по всем четным заданиям. Если такая структура не обнаружена, это значит что оп­росник в новой ситуации не работает и его не следует использо­вать традиционным способом.

В связи с этим нетрудно понять, почему факторный анализ так важен в психологии индивидуальных различий и психометрике. Один и тот же статистический аппарат может быть использован для конструирования тестов, разрешения теоретических споров по поводу количества и природы факторов, измеряемых тестами и опросниками, для проверки того, работают ли тесты так, как дол­жны, и законно ли использовать тот или иной тест в другой попу­ляции или в другой культуре. Возможно, вам даже захочется уз­нать, существует ли какая-нибудь связь между надежностью теста и величиной собственного значения фактора, полученного при факторизации теста, когда выделяется только один фактор.

В этой главе шла речь об основных принципах факторного анализа. Однако многие вопросы так и остались без ответа, и среди них следующие:

•Каким образом решать, сколько факторов должно быть выделе­но?

•Как может компьютерная программа в действительности выпол­нить факторный анализ?

• Какие типы данных целесообразно обрабатывать с помощью фак­торного анализа?

• Каким образом результаты, полученные в факторно-аналитичес­ких исследованиях, следует интерпретировать и представлять?

Эти и другие вопросы будут проанализированы в главе 15.

Предложения

о дополнительному чтению

Очень старая работа Айзенка по логическим основам факторного ана­лиза (Eysenck, 1953) вполне заслуживает прочтения; Чайлд (Child, 1990) и Клайн (Юте, 1994) предлагают два базисных, но доступных для пони­мания студентов варианта введения в факторный анализ.

Ответы на задания по самопроверке

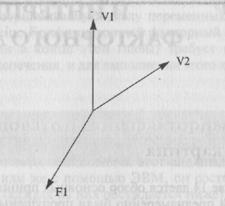
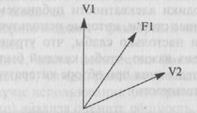
14.1. (а) Самый маленький угол между парой переменных на рис. 14.2 — это угол между V1 и V2. Следовательно, они имеют наиболее высокий уровень корреляции.

(б) Угол между переменными V3 и V2 равен приблизительно 270° (если двигаться по часовой стрелке). Табл. 14.3 показывает, что это соответствует корреляции, равной 0.

(в) Угол между переменными V5 и V3 равен приблизительно 210', что соответствует корреляции -0,87.

14.2. (а) Облическое решение — это таблица факторных нагрузок, при которых факторы не находятся под прямыми углами друг к дру­гу; они коррелируют между собой.

(б) Факторная нагрузка — это корреляция между переменной и фактором.

(в) Матрица факторной структуры — это таблица, показывающая корреляции между всеми переменными и всеми факторами.

(г) Ортогональное решение — это таблица факторных нагрузок, в которой все факторы не коррелируют между собой (т.е. нахо­дятся под прямыми углами друг к другу).

(д) Матрица взаимных корреляций факторов — это таблица, ко­торая представляет корреляции между всеми факторами в фак­торном анализе. Для ортогонального факторного анализа все корреляции между факторами будут равны нулю (так как они независимы). Для облического решения корреляции будут иметь значение больше нуля.

14.3. Собственное значение фактора представляет собой сумму воз­веденных в квадрат нагрузок этого фактора, вычисленную для всех переменных. Общность переменной — это сумма возве­денных в квадрат нагрузок по этой переменной, вычисленная по всем факторам.

(а) Общность переменной V2 есть 0,982 + О2 = 0,9604. Общности V3, V4, V5 и V6, подобно этому, составляют 0,82; 0,7325; 0,9604 и 0,7325, соответственно.

(б) Собственное значение фактора 2 равно 0,102 + 0,0г + (-0,102) + + 0,85г + 0,982 + 0,85г, или 2,4254.

(в) Поскольку имеется шесть переменных, фактор 2 объясняет

или 0,4042, вариативности между ними.

(г) Проанализированный в тексте пример показывает, что фак­тор 1 объясняет 0,423 вариативности. Поскольку факторы орто-

гональны, факторы 1 и 2 совместно описывают 0,43 + 0,4042 -0,834 вариативности между переменными.

(в) Изменение всех нагрузок между переменными и данным фактором приведет к тому, что фактор будет иметь корреляцию, равную -1,0, по отношению к его предшествующей позиции. Табл.14.3 показывает, что это соответствует его расположению в противоположном направлении (180*) по отношению к пред­шествующей позиции. Большие отрицательные корреляции между переменной и фактором подразумевают, что фактор указывает в сторону, противоположную направлению переменных, которые имеют самую большую корреляцию с ним. Изменение знака всех корреляций изменяет направление фактора таким образом, что он проходит через кластер переменных.

ВЫПОЛНЕНИЕ

И ИНТЕРПРЕТАЦИЯ

ФАКТОРНОГО АНАЛИЗА

Общая картина

Хотя в главе 14 дается обзор основных принципов факторного анализа, в ней преднамеренно были пропущены некоторые дета­ли, необходимые как для выполнения факторного анализа, так и для оценки методики адекватности публикуемых исследований. Многие журнальные статьи, которые используют факторный ана­лиз, методически настолько слабы, что утрачивают свое значе­ние, поэтому очень важно, чтобы каждый был способен распоз­навать такие исследования при обзоре литературы (делать поправ­ку на их несовершенность).

Главы, рекомендуемые

для предварительного чтения

14.

Введение

Несмотря на то что исследовательский факторный анализ можно выполнить вручную (и более старые работы, например, книга Кэттелла (Cattell, 1952), содержат детальную инструкцию для про­ведения подобных экспериментов), этим могут заниматься лишь энтузиасты или мазохисты, у которых имеется несколько свобод­ных недель. Вычисления, которые следует произвести, требуют много времени и изобилуют повторениями, поэтому лучше всего использовать компьютер. Большинство современных статистичес­ких пакетов программного обеспечения обладают достаточными возможностями для проведения исследовательского факторного

анализа в течение нескольких минут, а не часов. Время, необходи­мое для того, чтобы провести анализ, составляет величину, при­близительно пропорциональную числу переменных, возведенно­му в третью степень. Конфирматорный факторный анализ (кото­рый будет описан в конце этой главы) требует специального программного обеспечения, и для выполнения этого анализа иногда нужны часы.

Исследовательский факторный анализ

Независимо от того, выполняется этот вид анализа с исполь­зованием счётов или же с помощью ЭВМ, он состоит из восьми основных стадий (каждая из них обсуждается ниже).

Стадия 1. Убедитесь, что ваши данные подходят для фактор­ного анализа.

Стадия 2. Выберите модель — факторный или компонентный анализ.

Стадия 3. Решите, какое количество факторов необходимо выделить, чтобы представить ваши данные.

Стадия 4. В случае использования факторного (а не компонен­тного) анализа оцените общность каждой перемен­ной.

Стадия 5. Выделите факторы с учетом установленных общно-" стей (извлечение факторов).

Стадия 6. Вращайте эти факторы так, чтобы они прошли че­рез кластеры переменных, контролируя процесс получения «простой структуры».

Стадия 7. В случае необходимости подсчитайте факторные оценки.

Стадия 8. В случае необходимости проведите иерархический анализ, если он уместен.

Одна из проблем факторного анализа — это его мощность. Ис­пользуемые компьютерные программы почти всегда обеспечат тот или иной ответ, и, пытаясь анализировать данные с помощью самых разнообразных методов, выбирая разное количество фак­торов и концентрируясь на разных наборах переменных, можно «вытянуть» что-либо полуправдоподобное из самого скверного ис­следования. Время от времени сталкиваешься с журнальными ста-

тьями, в которых эта методика явно используется в отчаянных попытках спасти хоть что-нибудь из плохо организованного экс­перимента. Действительно, имеются некоторые области психоло­гии, такие, как. психология личных конструктов, в которых по­добная практика является нормой. Таким образом, крайне важно, чтобы те, кто использует методику или читает научную литерату­ру, имели представление об общей организации и выполнении факторно-аналитических исследований. В факторном анализе,как нигде, уместно изречение компьютерных специалистов: «мусор вносим, мусор выносим», поэтому данная глава начинается с обзора типов данных, которые могут быть с пользой обработаны факторным анализом.

Пригодность данных для факторного анализа

Не все данные могут быть подвергнуты факторному анализу. Он может быть применен, если соблюдаются следующие крите­рии.

1. Все переменные в анализе являются непрерывными, т.е. из­меряются по меньшей мере по трехбалльной интервальной шкале (такой, как «да/?/нет», кодируемой как 2/1/0). Обыч­но нельзя подвергать факторному анализу категориальные данные, которые образуют шкалу наименований, перечис­ляющую, например, цвет волос (черный/каштановый/ры­жий), страну проживания, предпочтение при голосовании, профессию. Иногда можно выбрать коды для категориальных данных, которые позволят преобразовать их в некоторый род интервальной шкалы, и она уже законно может быть под­вергнута факторному анализу. Например, поддержка комму­нистической партии может кодироваться «1», социал-демок­ратической партии — «2», консервативной/республиканской партии — «3» и партии правого крыла — «4». Эти числа фор­мируют шкалу доминирования «взглядов правого крыла», которая может быть подвергнута факторному анализу на за­конных основаниях.

2. Все переменные имеют (приблизительно) нормальное распре­деление, а асимметричные величины выделены и обработаны должным образом (см. например, книгу Табачника и Файдел-ла (Tabatchnick, Fidell, 1989, ch. 4). Асимметричные данные, если необходимо, могут быть преобразованы (см., например,

книги Табачника и Файделла (Tabatchnick, Fidell, 1989) или Хауэдла (Howell, 1992)).

3. Связи между всеми парами переменных приблизительно ли­нейны или по крайней мере не имеют очевидной U-образ-ной или J-образной формы.

4. Переменные независимы. Самый простой способ проверить это — просмотреть все статистические выражения и обеспе­чить, чтобы каждая измеряемая переменная отражала дей­ствие не более чем одной оценки из числа подвергающихся факторному анализу. Если у каждого индивидуума получены оценки по четырем заданиям теста, допустимо создавать и факторизовать новые переменные, такие как

или {(оценка 1 + оценка 2 — оценка 3) и 1 — оценка 4},

но не {(оценка I + оценка 2 + оценка 3) и (оценка 1 +

+ оценка 4)}

или {(оценка 1) и (оценка 1 + оценка 2 + оценка 3 + оценка 4)},

поскольку в последних двух случаях одна из наблюдаемых тестовых оценок («оценка 1») действует на две переменные, подвергающиеся факторизации. Вот общие случаи, когда этот принцип нарушается:

(а) факторизуется набор переменных, часть из которых -произведение от других переменных, также участвую­щих в анализе. Например, факторный анализ оценок по шести заданиям теста совместно с обобщенной оценкой индивидуумов по этим шести заданиям;

(б) вопросы, заданные в такой форме: «Вопрос 1: сколько будет 2 х 3?»

«Вопрос 2: чему равен ответ на первый вопрос, возве­денный в квадратную степень?»

Таким образом, если ответ на первый вопрос дан не­правильно, ответ на второй вопрос также должен быть неправильным.

Иногда выделить такие взаимозависимости бывает бо­лее трудным делом. Например, экспериментатор может

зарегистрировать отдельные показатели биотоков из раз­ных отделов мозга наряду с мышечной активностью из двух точек и намеревается подвергнуть факторному ана­лизу, средний показатель этих реакций вместе с некото­рыми заданиями опросника. Как знают читатели, име­ющие дело с психофизиологией, маловероятно, что все эти величины будут независимыми. Мышечные движе­ния (такие, как мигание глаз и биение сердца) могут обнаруживаться во всех записях физиологических про­цессов, если не предпринять специальных мер предос­торожности. Это может привести к тому, что различные электрические сигналы будут взаимозависимы и, сле­довательно, они не подходят для факторного анализа; (в) невозможно подвергать факторному анализу все оценки любого теста, в котором испытуемый не в состоянии получить предельно высокую (или предельно низкую) оценку по всем его шкалам (так называемые «ипсатив-ные тесты»), поскольку все шкалы в этих тестах обяза­тельно связаны отрицательными корреляциями. Сторон­ники этих тестов утверждают, что можно просто уда­лить одну из шкал перед факторизацией. Однако тогда интерпретация результатов будет зависеть от того, ка­кую шкалу мы (произвольно) изъяли.

5. Корреляционная матрица обнаруживает лишь несколько корреляций выше 0,3. Если все корреляции небольшие, сле­дует серьезно задуматься над тем, можно ли будет извлечь из матрицы какие-либо факторы. Если корреляции невели­ки из-за использования тестов с низкой надежностью, мо­жет быть, подойдет процедура корректировки эффектов ненадежности, как показано, в частности, Гилфордом и Фрачтером (Guilford, Fruchter, 1978). Подобно этому, если плохая организация эксперимента привела к тому, что дан­ные были собраны в группе с ограниченной представитель­ностью (например, оценки способностей были получены в выборке студентов университета, а не в выборке, взятой из общей популяции), для коррекции корреляций может ока­заться подходящим применение перед проведением фактор­ного анализа формулы Добсона (Dobson, 1988). Однако эти­ми фрагментами психометрического колдовства следует пользоваться с осторожностью, и на самом деле они не за-

меняют тщательно и глубоко продуманный план экспе­римента.

Тест сферичности Бартлетта (Bartlett, 1954) проверяет гипо­тезу, что все корреляции, расположенные вне диагонали, равны нулю, и это обычно вычисляют с помощью пакетов программ, таких, как SPSS. Однако этот тест очень чувстви­телен к размерам выборки, а маленькие корреляции между переменными в большой выборке приведут к тому, что тест укажет на уместность применения факторного анализа. На­много безопаснее просто визуально проанализировать кор­реляционную матрицу.

6. Пропущенные данные распределены по матрице данных слу­чайным образом. Было бы не очень разумно подвергать фак­торному анализу данные, где доля пропущенных значений в выборке охватывает полные блоки заданий. Например, одни испытуемые могут пройти тесты А, В и С. Другие могут пройти только тесты А и С, а остальные могут пройти только тесты В и С. По этой причине такие данные нельзя подвергать фак­торному анализу, хотя некоторые статистические пакеты сделают это без особого труда.

7. Любые пропущенные величины либо оценены (Tabatchnick, Fidell, 1989), либо в компьютерной программе заложена ко­манда игнорировать их. При введении данных в компьютер очень легко кодировать пропущенные значения числом «99» (или каким-либо другим), а затем забыть ввести в програм­му указание о том, что величина «99» представляет пропу­щенные данные. Такая ошибка, очевидно, лишит законной силы весь анализ.

8. Большая выборка испытуемых. Эксперты дают различные рекомендации, однако не следует пытаться применять фак­торный анализ, если число испытуемых меньше 100, посколь­ку стандартные ошибки корреляции в этом случае окажутся неприемлемо велики. Это означает, что корреляционная мат­рица небольшой выборки испытуемых практически не будет похожа на «подлинную» корреляционную матрицу. Другими словами, анализ, базирующийся на маленьких выборках, вряд ли будет воспроизводимым, но он также не будет в доста­точной степени соответствовать реально существующим вза­имосвязям между переменными. Обычно считается, что не­обходимо связать размер выборки с числом переменных, под-

23 -

вергающихся анализу. Например, Нанелли (Nunnally, 1978) придерживается точки зрения, что испытуемых должно быть по крайней мере в 10 раз больше, чем переменных. Более поздние исследования, такие, как работы Барретта и Клай-на (Barrett, Kline, 1981) и Гваданоли и Велисера (Guadagnoli, Velicer, 1988), показывают, что в случае, если испытуемых больше, чем переменных, само отношение числа испытуе­мых к числу переменных не так важно, как абсолютный раз­мер выборки и величина факторных нагрузок. Следователь­но, если факторы хорошо определены (например, с нагруз­ками 0,7, а не 0,4), экспериментатору нужна меньшая выборка, чтобы выделить их. Если известно, что анализиру­емые данные отличаются высокой надежностью (например, тестовые оценки, а не ответы на отдельные задания), то эти ограничения можно в некоторой степени ослабить. Однако попытки проводить факторный анализ на небольших набо­рах данных (таких, как репертуарные решетки) обречены на провал, поскольку большая стандартная ошибка корреля­ций гарантирует, что факторное решение будет и произволь­ным, и невоспроизводимым.

Проблема возникает при дихотомических данных, т.е. в тех слу­чаях, когда оценки могут принимать только одно из двух значений. Такие данные часто встречаются при анализе ответов на задания теста (1 = «да», 0 = «нет» или 1 - «правильный ответ», 0 = «непра­вильный ответ»). Когда дихотомические задания коррелируют между собой, корреляции могут достичь 1 только в случае, если оба зада­ния теста имеют приблизительно одинаковые уровни сложности. Таким образом, небольшая корреляция может означать, что

• не существует связи между заданиями сходного уровня слож­ности,

или

• два задания имеют сильно различающиеся уровни сложности. Таким образом, факторный анализ обычных пирсоновских кор­реляций между дихотомическими заданиями обнаруживает тен­денцию порождать факторы «трудности задания», поскольку только задания, близкие по уровню сложности, могут, вероятно, корре­лировать между собой и формировать фактор. Иные задания, ко­торые измеряют тот же самый конструкт, но имеют другие уров­ни сложности, будут по этой причине обнаруживать низкие на-

грузки по результирующему фактору. Однако чрезвычайно слож­но обойти эту проблему, используя стандартный статистический пакет, который не предлагает альтернативы использованию пир­соновских корреляций. Существуют и другие типы коэффициен­тов корреляций, которые позволяют избежать этих проблем, и Чамберс (Chambers, 1982) дает полезное, хотя и излишне насы­щенное техническими деталями, краткое описание литературы. Законность факторизации таких коэффициентов все еще обсуж­дается (Vegelius, 1976), хотя большинство исследователей обычно проделывают эту процедуру. Короче говоря, жизнь станет намно­го легче, если можно будет избежать использования дихотомичес­ких данных.

Задание для самопроверки 15.1

Психолог изучает математические навыки в выборке, состоящей из 100 одиннадцатилетних детей; это является частью ее дипломной работы. Она собрала данные по 120 заданиям теста, каждое из кото­рых она оценивала как правильный или неправильный ответ. Она так­же учитывала место жительства (графство) каждого участника и на­меревалась использовать факторный анализ этих ответов, чтобы за­ново выявить основную структуру математических способностей и установить, не выше ли математические способности детей в одних графствах по сравнению с другими. Какой совет вы могли бы ей дать?

Факторный анализ

или компонентный анализ

*

Одна научная школа поддерживает точку зрения, что фактор­ный (но не компонентный) анализ никогда не должен использо­ваться из-за трудности установления общностей и чрезвычайной сложности определения факторных оценок. Другая школа придер­живается взгляда, что, поскольку факторная модель априори с гораздо большей вероятностью соответствует данным, должна при­ветствоваться любая попытка оценить общности. С этих позиций модель главных компонент просто не соответствует заданиям теста и другим данным, которые, как следует ожидать, содержат уни­кальную вариативность. Некоторые авторы, например, Кэрролл (Carroll, 1993), полагают, что бессмысленно использовать модель главных компонент, так как известно, что она не соответствует типу данных, которые обычно анализируются, хотя многие из нас утверждают, что на практике не имеет особого значения, какая

методика применяется, поскольку разные методы анализа редко дают сильно различающиеся результаты. Заинтересованные чита­тели должны посмотреть работу Велисера и Джексона (Velicer, Jackson, 1990) для более детального обсуждения этой темы.

Тесты для определения количества факторов

Разработано несколько способов, помогающих исследователям выбрать «правильное» количество факторов. Они требуют осторож­ного обращения: при принятии этого важного решения нельзя полагаться на компьютерные программы, поскольку известно, что большинство из них (в частности SPSS) используют методы, ко­торые оказываются несостоятельными и не могут включить неко­торые из наиболее полезных тестов. Определение количества выде­ляемых факторов, вероятно, — наиболее важное решение, кото­рое необходимо принять, когда проводишь факторный анализ. Ложное решение может привести к бессмысленным результатам при обработке самого четкого набора данных. Можно попытаться выполнить несколько вариантов анализа, базирующегося на раз­ном количестве факторов, и использовать несколько различных тестов, определяющих выбор факторов.

Первые руководящие указания дают теория и прошлый опыт. Иногда может возникнуть желание использовать факторный ана­лиз, чтобы убедиться, что тест работает в соответствии с ожида­ниями, будучи использован в другой культуре, группе больных или каким-либо другим способом. В этих целях может проводиться конфирматорный факторный анализ (см. ниже), но если иссле­довательский факторный анализ является более предпочтитель­ным, предыдущие результаты могут быть использованы в качестве ориентиров в определении того, сколько факторов надо выделять. Если проведенный в США факторный анализ теста (методически адекватный) выявил семь факторов, то любая попытка подверг­нуть тест факторному анализу в другой культуре должна рассмот­реть как минимум семифакторное решение.

Безусловно, и теория, и прошлый опыт имеют позитивное значение, но в большинстве случаев факторный анализ действи­тельно является, по сути, исследовательской методикой. Иссле­дователь часто не будет иметь весомых теоретических оснований для решения вопроса о том, сколько факторов следует выделить, а предшествующие исследования иногда методически настолько

несовершенны, что оказываются бесполезными. Существует ряд других приемов, которые могут быть использованы в этих обсто­ятельствах, все они направлены на определение количества фак­торов, которые следует извлекать из корреляционной матрицы. Проблема состоит в том, что некоторые из них, будучи включены в компьютерные пакеты, попадают иногда в руки неопытных пользователей, поэтому оказываются просто бесполезными. Кро­ме того, различные методики не всегда дают совпадающие ре­зультаты: один тест может указывать на шесть факторов, другой — на восемь, а предыдущее исследование — на девять! При таких обстоятельствах самое безопасное — рассматривать несколько ре­шений и проверять их на психологическую пригодность. Пользо­ватели должны установить также:

• не способствует ли увеличение количества факторов упро­щению решения (например, уменьшению доли нагрузок в диапазоне от ~0,4 до 0,4). Если увеличение количества фак­торов не влияет на простоту решения (или очень незначи­тельно его упрощает), то его применение скорее всего не имеет смысла;

• не появляются ли какие-либо большие корреляции между факторами при осуществлении облических вращений. Пос­леднее может указывать на то, что было извлечено слишком много факторов и два из них пытаются пройти через один и тот же кластер переменных. Об этом могут косвенно свиде­тельствовать корреляции между факторами, которые будут больше приблизительно 0,5;

• не разделились ли какие-либо хорошо известные факторы на две или более частей. Например, если во множестве пред­шествующих исследований было показано, что набор зада­ний формирует только один фактор (например, экстравер­сию), а в вашем анализе они все же формируют два факто­ра, это говорит о том, что было, вероятно, извлечено слишком много факторов.

Один из старейших и наиболее простых тестов для определе­ния количества факторов — это тест, описанный Кайзером (Kaiser, 1960) и Гуттманом (Guttman, 1954) и известный как «критерий Кайзера—Гуттмана». Его преимуществом является простота испол­нения. Надо просто провести анализ данных методом главных ком­понент, выделив столько факторов, сколько существует перемен-

ных, но без проведения операции, известной как «вращение» (она будет обсуждаться ниже). Собственные значения факторов вы­числяются, как обычно, сложением квадратов нагрузок по каждо­му компоненту. После этого надо просто посчитать, сколько фак­торов имеют собственные значения выше 1,0 — это и есть количе­ство факторов, которое можно использовать.

Существует немало проблем с использованием этой методики; наиболее очевидная из них связана с ее чувствительностью к ко­личеству переменных, взятых для анализа. Поскольку каждое соб­ственное значение — это просто сумма квадратов факторных на­грузок, при увеличении количества переменных должно увеличи­ваться и собственное значение. Тест на определение количества факторов должен давать один и тот же результат, независимо от того, четыре или 40 переменных представлены в каждом факторе, а критерий Кайзера—Гуттмана явно не действует таким образом. Более того, Хакстиан и Мюллер (Hakstian, Mueller, 1973) отмеча­ли, что данная процедура на предназначена для определения ко­личества факторов. Поскольку его исключительно легко проводить автоматически, большинство статистических пакетов будут выпол­нять тест Кайзера—Гуттмана как задаваемый по умолчанию. Тем не менее этот тест следует всегда отвергать.

Тест «каменистой осыпи» («scree test»), предложенный Кэт-теллом (Cattell, 1966), концептуально тоже прост. Так же как и критерий Кайзера—Гуттмана, он базируется на собственном зна­чении факторов, полученных в результате применения метода глав­ных компонент, не прошедших вращение. Однако он учитывает относительные величины собственных значений факторов, и по­этому не должен быть чувствителен к вариациям в количестве ана­лизируемых переменных. Этот тест основывается на зрительном изучении графика, представляющего последовательные собствен­ные значения факторов, так как это показано на рис. 15.1. График должен быть построен с максимально возможной аккуратностью с использованием специальной бумаги или графопостроительной программы. Точность графиков, производимых некоторыми стати­стическими пакетами, недостаточна для этой цели.

Основная идея проста. Очевидно, что точки в правой стороне рис. 15.1 образуют прямую линию, называемую «склон». Можно про­ложить через эти точки линейку и определить, сколько собственных значений факторов явно располагаются над этой линией —- это и есть количество факторов, которые должны быть извлечены.

Рис. 15.1. Тест «каменистой осыпи», демонстрирующий собственные значения факторов, полученных в результате анализа главных компонент девяти переменных до вращения матрицы. График показывает, что следует извлечь два фактора.

Рис. 15.1 представляет двухфакторное решение. Дальнейшие при­меры использования тестов такого типа были даны Кэттеллом (Cattell, 1966) в главе 5 книги Кэттелла (Cattell, 1978) и Кэттел­лом и Фогельманом (Cattell, Vogelman, 1977). Несколько широко распространенных пособий по факторному анализу описывают этот тест неправильно, утверждая, что количество факторов соответ­ствует количеству собственных значений факторов, располагаю­щихся над прямой линией, плюс еще один. Таким образом, в при­веденном выше решении они стали бы настаивать на выделении трех факторов. Не очень понятно, как возникло это недоразуме­ние, поскольку в статьях Кэттелла и в его книге, вышедшей в 1978 г., совершенно ясно говорится по этому поводу: «Последний реальный фактор — это тот фактор, который обнаруживается пе­ред тем, как график превращается в горизонтальную прямую ли­нию» (Cattell, Vogelman, 1977).

Проблема теста «каменистой осыпи» заключается в том, что он полностью основывается на субъективных суждениях и может иногда иметь несколько возможных интерпретаций, особенно когда размер выборки или «выступающие» факторные нагрузки невели­ки (Gorsuch, 1983). Иногда на графике обнаруживается более чем

один четко идентифицируемый излом прямой линии. В таких случаях необходимо просто просмотреть собственные значения факторов, которые расположены над крайним слева отрезком прямой линии. Хорошая методика для определения количества извлекаемых факторов — МАР-тест (Velicer, 1976). В вычислительном отноше­нии она слишком сложна, чтобы выполнять ее вручную, но она не включена в основные коммерческие пакеты для выполнения факторного анализа, несмотря на то что является одной из наи­более признанных точных методик (Zwick, Velicer, 1986). Суще­ствует несколько других подходящих методов, но они тоже оста­ются не введенными в главные пакеты. Компьютерные моделиру­ющие исследования показали, что в отсутствие МАР-теста тест «каменистой осыпи», вероятно, представляет наиболее точный руководящий принцип для принятия всех важных решений по поводу количества факторов, извлекаемых из корреляционной матрицы.