Актуальность технического обслуживания 16 страница
Например, предположим, мы постулируем наличие двух факторов — общего интеллекта (g) и тестовой тревоги (ТА). Предположим также, что оценки по некоему тесту (тест 1) находятся яод влиянием обоих этих факторов, но влияние общего интеллекта
больше, чем влияние тестовой тревоги. Мы можем представить это в виде простого уравнения типа:
Тест 1 - 0,8 х g + 0,1 х ТА + уникальная дисперсия.
Числа 0,8 и 0,1 показывают степень связи между переменными и каждым фактором — факторные нагрузки. Каждое из этих чисел может быть:
• определено непосредственно в виде числа (как в приведенном выше примере);
• установлено с помощью компьютерной программы;
• принято равным другим величинам, которые уже установлены. Например, можно считать, что все тесты находятся под влиянием тестовой тревоги в равной, но неизвестной степени. (Такая возможность выбора на практике может быть проблематичной.)
В конфирматорном факторном анализе обычно уравнение пишется для каждой переменной, показывая, какой фактор (или факторы) предположительно влияет на показатели по этой переменной, хотя, как правило, не устанавливается размер нагрузок. Любые факторные нагрузки, которые не определены, принимаются равными 0. Необходимо указать также на то, что дисперсия каждого фактора равна 1,0. Затем компьютерная программа устанавливает наилучшие возможные значения для каждой из нагрузок и также вычисляет статистики, показывающие, насколько полно постулируемая структура соответствует реальным данным. Обычная практика состоит в том, чтобы попытаться применить несколько различных моделей и выбрать одну, которая дает наибольшее соответствие, т.е. ту, которая лучше всего подтверждается данными.
Лоелин (Loehlin, 1987) приводит подробное обсуждение того, как интерпретировать различные показатели соответствия модели. Хотя показатели соответствия полезны для того, чтобы сделать выбор между конкурирующими моделями, они не особенно эффективны для выработки абсолютных критериев соответствия определенной модели. Это означает, что методика не способна с легкостью установить, будут ли выявлены в полученных данных какие-либо определенные паттерны факторов и факторных нагрузок, но она может быть полезна при выяснении степени конкурентоспособности этих моделей.
Обычно практикуется представлять связи между переменными, общими факторами и уникальными факторами с помощью

Рис. 15.5. Диаграмма путей, демонстрирующая, как два коррелирующих фактора (F1 и F2) влияют на значения шести наблюдаемых переменных (от VI до V6). Представлены также уникальные дисперсии переменных-(от U1 до U6).
диаграммы, называемой «диаграмма путей». Пример должен сделать это более понятным.
На рис. 15.5 представлены два фактора F1 и F2, каждый из которых, предположительно, влияет на переменные (от VI до V6), на числа пока не обращайте внимания. Вы можете заметить, что V4 находится под влиянием обоих факторов, а на другие переменные влияет только один из них. На диаграмме показаны также уникальные дисперсии каждой переменной (от U1 до U6). Каждая линия, связывающая фактор с наблюдаемой переменной, имеет стрелку на одном конце, указывающую, что по допущению фактор обусловливает определенную наблюдаемую переменную (а не наоборот). Кривая, соединяющая фактор 1 и фактор 2, представляет корреляцию, т.е. факторы 1 и 2 коррелируют между собой. Таким образом, эта диаграмма соответствует облическому факторному решению.
Числа, расположенные на каждой из линий, представляют собой числовые значения факторных нагрузок (в матрице фактор-
Таблица 15.3
Матрица факторной модели, эквивалентная диаграмме путей, помещенной на рис. 15.5
| Переменные | Фактор 1 | Фактор 2 | Аг |
| VI | 0,8 | 0,0 | 0,64 |
| V2 | 0,7 | 0,0 | 0,49 |
| V3 | 0,8 | 0,0 | 0,64 |
| V4 | 0,6 | 0,5 | 0,61 |
| V5 | 0,0 | 0,7 | 0,49 |
| V6 | 0,0 | 0,7 | 0,49 |
ных паттернов), или, если это кривая линия, такие числа обозначают корреляции между этими факторами. Однако в большинстве случаев все числа будут установлены программой. Так, диаграмма путей на рис. 15.5 соответствует матрице факторных паттернов, представленной в табл. 15.3.
Несколько других вероятных диаграмм путей может быть построено на основе теории или предшествующего исследования, и каждую можно проверить, чтобы определить, насколько полно она соответствует данным. Таким способом исследователь может осуществить выбор между различными теоретическими конкурирующими моделями. Однако здесь существует определенный риск, связанный с использованием этих методов. Слишком легко пуститься в «рискованное предприятие», модифицируя модель снова и снова, чтобы улучшить уровень ее соответствия, независимо от ее психологического правдоподобия. Действительно, компьютерные пакеты EQS и LISREL одобряют эту практику, подсказывая, какие части модели нуждаются в модификации. Однако компьютерная программа ничего не знает о психологии или теории факторного анализа и нередко будет предлагать что-то, лишенное смысла, допуская, например, чтобы уникальные вариативности различных переменных коррелировали между собой. Такая модель может исключительно хорошо соответствовать данным, полученным на определенной выборке, и тем не менее иметь мало психологического смысла (и маловероятно, что она будет воспроизведена на других выборках). Однако всегда, когда есть необходимость выбора между конкурирующими теоретическими моделями, кон-
фирматорный факторный анализ может оказаться очень полезным инструментом.
Представленное выше описание было намеренно упрощено, и читатели, которые собираются использовать этот метод, прибегая к другим источникам, должны усвоить:
• что этот анализ обычно проводится на материале ковариа-ций, а не корреляций
и
• что именно подразумевается под «идентификацией» модели.
Резюме
Факторный анализ — это исключительно полезный метод для прояснения связей между некоторым количеством переменных, измеренных в интервальноу шкале или шкале отношений. Он может быть применен к любым данным такого рода — от физических или физиологических показателей до заданий опросников. В этой главе было описано, как проводить технически обоснованный факторный анализ, и были четко обозначены некоторые общие ошибки, иногда проникающие в публикуемые статьи. Наконец, в ней был представлен конфирматорный факторный анализ как полезный метод для выбора между различными конкурирующими факторно-аналитическими моделями.
Предложения
по дополнительному чтению
Их дано достаточно много в тексте. Книги Чайдда (Child) и Клайна (Kline) наиболее просты, книги Горсача (Gorsuch) и Комрея (Comrey) также весьма приемлемы для читателей, не имеющих математической подготовки.
Ответы на задания по самопроверке
15.1. В связи с этим предложением возникают проблемы, наиболее очевидная из которых состоит в том, что «место жительства» — это переменная, которая не может быть измерена по шкале интервалов. Когда устанавливаются числовые коды, полностью произвольным является присвоение «1» Корнуоллу или Камб-
рии, поэтому коды не образуют какую-либо шкалу. Следовательно, они должны быть исключены из факторного анализа. (Чтобы выявить различия в математических способностях между учащимися графств, вы могли бы предложить коллеге вычислить факторные оценки по каждому из факторов, а затем провести анализ вариативности, используя «графство» как межиндивидуальный фактор.)
Другая проблема состоит в том, что в анализ включено больше переменных, чем имеется испытуемых в выборке. Таким образом, хотя количество испытуемых больше, чем «магическое» число 100, эти данные не годятся для факторного анализа. Вы могли бы предложить вашей коллеге собрать несколько больше данных, для того чтобы увеличить размер выборки по крайней мере до 150. Полезно было бы предупредить ее также о тех проблемах, которые связаны с факторизацией дихотомических данных, когда единственно возможным ответом является 0 или 1. Если обнаружится, что задания коренным образом отличаются по степени сложности (которая отражается в пропорции индивидуумов, правильно отвечающих на каждое задание), вы могли бы обратиться к литературе с целью поиска альтернатив корреляции Пирсона, которые подходят для факторного анализа. Наконец, вам было бы полезно проверить вместе с вашей коллегой, что детям было дано достаточно времени, чтобы попытаться решить все задания теста, и установить, кодировались ли задания, которые они не пытались решить, так же как и задания, которые решены неправильно, или этим заданиям давали особый код и рассматривали их как отсутствующие данные. Если заданиям, которые дети не пытались решить, давали такой же код, "ак и «неправильному ответу» (например, "О»), становится ясным, что могут возникнуть проблемы в том случае, если не всем детям удалось закончить тест в отведенное время. Задания, расположенные в конце теста, будут казаться более трудными, чем они есть на самом деле, просто потому, что только некоторым детям удастся дойти до них. В подобных обстоятельствах, возможно, было бы лучше просто проанализировать первые 50 заданий (или около того), в таком случае отпадает необходимость собирать дополнительные данные, поскольку выборка из 100 испытуемых была бы адекватна такому числа заданий.
15.2. Три и четыре. Вам следует, вероятно, выделить три фактора, имея в виду, как было установлено, что тест «каменистой осыпи» действует лучше, чем метод Кайзера—Гуттмана.
15.3. Простая структура — показатель того, насколько точно каждый фактор проходит через кластер переменных. Предположим, что факторы сохраняют положение под прямыми углами, представ-
ляя ортогональное вращение. Если с помощью вращения была достигнута простая структура, то каждый фактор будет иметь несколько высоких корреляций (выше 0,4 или ниже -0,4) между некоторыми переменными и корреляции, которые близки к нулю (например, плюс/минус 0,1) между всеми остальными. При этом должно быть очень немного корреляций средней величины в диапазоне плюс/минус 0,1-0,4. Если также проанализировать строки факторной матрицы, то каждая переменная должна иметь большую нагрузку только по одному или двум факторам. В значительной степени такое же положение существует для вариантов облического вращения (в котором факторы расположены не под прямым углом) за исключением того, что «матрица факторных паттернов», которая используется, чтобы определить простоту решения, не содержит корреляций между переменными и факторами, хотя интерпретируется таким же образом. Поскольку исходная позиция факторов по отношению к переменным, по сути, произвольна, то если не проводилось вращение, приводящее к простой структуре, различные исследователи будут сообщать о весьма разных результатах. Таким образом, важно обеспечить стабильную идентификацию факторов, получаемых в разных исследованиях.
- , - -• '• ....... ' ' :,:'
15.4. Факторный анализ будет показывать природу и степень перекрытия между оценками теста и, вероятно, приведет к появлению нескольких факторов, измеряющих личностные особенности и/или способности. Оценки можно вычислить для соискателя по каждому из этих факторов («факторные оценки»), и каждая из этих факторных оценок может быть валидизирована таким же способом, как валидизируются тесты и как это было показано в главе 13. Например, за соискателями могут вести тщательное наблюдение и коррелировать их факторные оценки с показателями продуктивности, или рангами, которые им выставляет инспектор за выполнение работы. Чтобы определить любые различия в факторных оценках между разными группами рабочих, например тех, кто медленнее продвигается по службе, или тех, которые уволились может быть использована ANOVA. Если некоторые из факторных оценок действительно окажутся полезными в процессе отбора, тесты, имеющие высокие нагрузки по этим факторам, с пользой могут быть сохранены. Те же, которые не будут нагружать ни один из полезных факторов, можно, вероятно, изъять из батареи оценок.
ТЕОРИЯ СЛОЖНОСТИ ЗАДАНИЙ*
Общая картина
Эта глава представляет подход, полностью отличный от оценки способностей с помощью тестовых баллов, — подход, который не требует использования норм и даже не настаивает на том, чтобы респонденты выполняли одни и те же тесты. Как следует из названия, эта методика учитывает, каким образом люди отвечают на отдельные задания в тесте, а не их общие оценки. Она естественным образом приводит к специально разработанному «пошаговому» тестированию, в котором трудность предъявляемых заданий подбирается в соответствии с уровнем способностей каждого индивидуума; это требует, естественно, предъявления заданий теста с помощью компьютера, и это — одно из наиболее впечатляющих недавних достижений психометрики. «
Главы, рекомендуемые для предварительного чтения
11 и 12.
До сих пор мы полагали, что общая оценка человека по психологическому тесту обеспечивает лучшее измерение его способностей или наличия у него какой-либо особенной личностной черты.
* В книге К. Купера эта глава называется «Item response theory» — «Теория ответов на задания», что в переводе на русский язык не имеет научного содержания. Поэтому мы сочли возможным озаглавить эту часть, исходя из смысла излагаемого в ней психодиагностического подхода. (Прим. перев, и науч. ред.)
Нам настолько привычна процедура суммирования количества заданий, на которые получены правильные ответы (или общего подсчета баллов по шкалам Ликерта), и сравнение этих оценок с нормами для интерпретации их значения, что бывает трудно увидеть ошибочность некоторых методов обработки, тестов и способы их усовершенствования.
Проблема, связанная с использованием обшей оценки в качестве показателя способностей, состоит в том, что тот, кто отвечает правильно на четыре легких задания, но оказывается не в состоянии решить все трудные, заканчивает тест с таким же результатом, как и тот, кто (преодолевая скуку?) правильно отвечает на одно легкое задание и на три трудных, что представляется неверным, поскольку общая оценка полностью игнорирует информацию (легко получаемую) о трудности каждого задания теста. Индивидуумы получат высокий балл при наличии легкого теста и низкий балл, если им дадут трудный тест, хотя они обнаруживают одни и те же способности в каждом тесте. Все это и делает необходимым использование норм.
Разумеется, существует немало альтернатив вычислению общей оценки как показателя способностей человека. Если уровни трудности («р-значения», т.е. пропорция индивидуумов, выполняющих задания) известны, можно, конечно, использовать р-значения наиболее трудного задания, на которое был получен правильный ответ (или р-значения самого легкого задания, на которое ответили неправильно), как показатель способностей. В качестве альтернативы можно вычислить среднюю трудность заданий, на которые были даны правильные ответы. Существует множество возможностей, большая часть которых остается неисследованной в литературе.
(а) Определите общий балл и другие три показателя способностей для испытуемого 2.
Задание для самопроверки 16.1
Цель этого упражнения — побудить вас задуматься над тем, каким образом статистические характеристики, иные, нежели общая оценка, могут отразить уровень способностей человека; они включают одну характеристику, базирующуюся на трудности самого сложного задания из решенных, и другую, базирующуюся на самом легком задании, которое не удалось решить. В приведенной таблице показаны ответы двух индивидуумов на девять заданий теста, которые предъявлялись большой выборке людей. Р-значения показывают долю людей, которые ответили на каждое задание правильно.
| Задание | ' 1 | 2 3 4 | 5 6 | |
| ^-значение 0,9 | 0,1 0,4 0,5 | 0,7 0,4 | 0,3 0,8 0,3 | |
| Исп. 1 | 0 1 0 | 1 0 | 0 1 0 | |
| Исп.2 | 0 0 | 0 1 0 | ||
| Общий показатель | / - мин. р-зна- 1 — макс, р-зна-чение правильных чение неправильных | / - среднее р-зна-чение правильных | ||
| решении | решении | решении | решении | |
| Исп. 1 | 4 ' | 1 - 0,4 = 0,6 | 1 -0,5 = 0,5 | 2,8 1-— = 0,30 4 |
| Исп.2 |
(б) Почему может быть нецелесообразно оценивать способности на основе критерия, ориентированного на «самое трудное решенное задание» или на «самое легкое нерешенное задание»?
Проблема заключается в том, что очень большое число показателей может быть подсчитано на основе данных, представленных в задании 16.1. Как решить, какой из показателей следует использовать? Один подход может заключаться в применении имеющейся математической модели, описывающей, что может происходить, когда испытуемый отвечает на задания теста. Для простоты мы примем пока допущение, что имеем дело с тестом свободных ответов (тогда угадывание не составляет проблемы), каждое задание которого может быть оценено как правильно или неправильно решенное.
Характеристическая
кривая задания
....
Три допущения, которые можно сделать с достаточной степенью надежности, таковы:
1) вероятность того, что кто-то справится с заданием правильно, зависит как от способностей человека, так и от трудностей тестового задания;
2) вероятность того, что кто-то справится с конкретным заданием правильно, не зависит от правильности его ответов на любые другие задания, а является функцией способностей человека (это известно как допущение «локальной независимости»);
3) все задания шкалы оценивают только один конструкт.
Допущение локальной независимости, в сущности, означает, что каждое задание должно представлять совершенно новую проблему и не должно быть переноса с одного задания на следующее — либо положительного (когда правильный ответ на один вопрос или сам по себе необходим, или дает ключ к ответу на другой), либо отрицательного (когда может быть необходимо отказаться от «приема», использованного в предыдущих вопросах, чтобы прийти к правильному ответу в следующем). Таким образом, допущение локальной независимости не будет распространяться на такие задания, как задание 1: «Сколько будет 4 + 5?» и задание 2: «Чему будет равен корень квадратный из ответа на задание 1?», поскольку, если на задание 1 ответили неправильно, ответ на задание 2 также должен быть ошибочным. Ради простоты давайте рассмотрим одиночное тестовое задание. Допущение (1), приведенное выше, говорит о том, что вероятность того, что кто-то правильно справится с заданием, зависит от его способностей и трудности этого задания. Итак, каков же наилучший способ смоделировать эту связь математически? Вы можете сначала подумать, что прямая линия, связывающая способности и успешность, обеспечит самую простую взаимосвязь. В конце концов, специалисты в области психометрики обычно допускают возможность линейных связей между переменными, когда вычисляют корреляции и т.д. Таким образом, может быть, мы могли бы описать связь между способностями и успешностью решения задания прямой линией? Один такой график представлен на рис. 16.1 (не обращайте пока внимания на буквы А, Си В).
На рис. 16.1 показано, что мы можем оценить вероятность того, что кто-то выполнит задание, используя уравнение прямой, т.е.
вероятность решения задания = а + b x способности, где а и b — константы (числа), которые могут быть установлены, например, с помощью регрессии. К сожалению, этот график, по-видимому, является в значительной степени ошибочным. Во-первых, мы знаем, что вероятность правильного решения задания
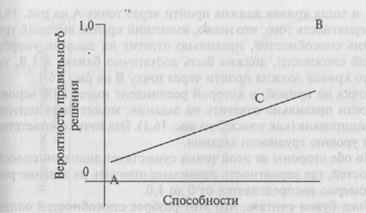
Рис. 16.1. Возможная линейная связь между способностями и успешностью выполнения задания.
может колебаться только между 1 и 0. В отличие от тех случаев, когда линия не горизонтальна (что само указывает на то, что вероятность решения заданий совершенно не связана со способностями), прямая линия обязывает предположить, что у студентов с очень низким или с очень высоким уровнем способностей вероятность решения задачи будет либо меньше нуля, либо больше единицы, и это явно абсурдно. Здесь же возникает и вторая проблема. Положение линии на рис. 16.1 определяется двумя параметрами: ее наклоном и высотой (по оси Y), и, значит, оба параметра должны быть установлены, когда оценивается взаимосвязь между способностями и успешностью решения задания. Может быть, существует лучший способ описания этой связи — способ, который не допустит, чтобы вероятность оказалась меньше 0 или больше 1 и который основывается на одном параметре. Ради упрощения предположим, что мы имеем дело с тестом свободного ответа, в котором респондентов просят дать один конкретный ответ (например: «Какой город является столицей Эквадора?») вместо нескольких альтернативных ответов, из которых нужно сделать выбор (например: «столица Эквадора — (а) Кито; (б) Богота; (в) Монтевидео»). При этом условии представляется разумным сделать следующие допущения.
• Вероятность того, что некто, имеющий крайне низкий уровень способностей, правильно ответит на тестовые задания умеренной сложности, должна быть достаточно близкой к
О, и тогда кривая должна пройти через точку А на рис. 16.1.
• Вероятность того, что некто, имеющий крайне высокий уровень способностей, правильно ответит на задания умеренной сложности, должна быть достаточно близка к 1,0, так что кривая должна пройти через точку В на рис. 16.1.
• Точка на кривой, в которой респондент имеет 50% вероятности правильно ответить на задания, может быть идентифицирована (как точка С на рис. 16.1). Эта точка соответствует уровню трудности задания.
• По обе стороны от этой точки существует диапазон способностей, где вероятность правильно ответить на задание равномерно распределяется от 0 до 1,0.
• Пока будем считать, что этот разброс способностей одинаков для каждого задания.
При наличии этих ограничений, в известной степени обусловленных здравым смыслом, я предполагаю, что форма кривой, связывающей способности с успешностью решения заданий, могла бы выглядеть приблизительно так, как это показано на рис. 16.2. Этот рисунок представляет "вероятность правильных ответов на задание для индивидуумов с различным уровнем способностей. Уровень трудности этого задания составляет 1,0, что соответствует точке на оси X, в которой индивидуум имеет 50% вероятности ответить на задание правильно. Графики такого типа известны как характеристические кривые задания (ХКЗ) (item characteristic curves (ICCs)) — это очень важный термин.
Вы могли заметить, что шкала способностей имеет как положительные, так и отрицательные значения. Не беспокойтесь об этом.
Можно видеть, что шансы правильно ответить на это задание у человека, уровень способностей которого ниже —1,5, весьма незначительны, а при уровне способностей выше 3,5 подавляющее большинство людей ответят на это задание правильно. Разные задания теста обычно будут иметь различные уровни трудности, и их можно удобно представить на одном и том же графике, как показано на рис. 16.3, который представляет три задания с уровнями трудности 0, 2, 3.
Задание для самопроверки 16.2
Представьте себе, что некто, имеющий уровень способностей, равный 1,0, ответил на три задания, характеристические кривые которых (ХКЗ) даны на рис. 16.3. Каковы приблизительно шансы, что он смо-
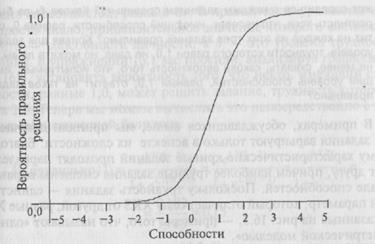
Рис. 16.2. Характеристическая кривая задания, уровень трудности которого составляет 1,0.
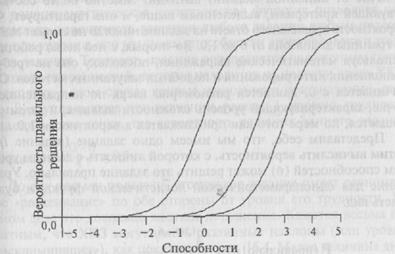
Рис. 16.3. Три характеристических кривых заданий, уровень трудности которых составляет 0, 2, 3.
жет справиться с каждым заданием правильно? Какова была бы вероятность того, что человек, имеющий способности, равные 0, ответит на каждое из этих трех заданий правильно? Кривая для задания, уровень трудности которого равен 1,0, не дана, но можете ли вы, тем не менее, сказать, какова вероятность того, что испытуемый, имеющий уровень способностей, равный 1,0, ответит на такое задание правильно?
В примерах, обсуждавшихся выше, мы приняли допущение, что задания варьируют только в аспекте их сложности. Благодаря этому характеристические кривые заданий проходят параллельно друг другу, причем наиболее трудные задания смещены вправо по шкале способностей. Поскольку трудность задания — единственный параметр, который отличает одну ХКЗ от другой, разные ХКЗ, показанные на рис. 16.3, — примеры того, что называют «однопа-раметрической моделью».
Графики, изображенные на рис. 16.2 и 16.3, могут быть описаны довольно простым математическим уравнением, известным как «логистическая функция». Существует две главные причины для работы с логистической функцией. Во-первых, форма кривой (в отличие от линейной модели) выглядит заметно более соответствующей критериям, выделенным выше, и она гарантирует, что вероятность правильного ответа на задание никогда не сможет выйти за границы диапазона от 0 до 1,0. Во-вторых, с ней легко работать, используя математические выражения, поскольку она не требует выполнения интегрирования и подобных запутанных методов. Она начинается с 0, двигается равномерно вверх по направлению к точке, характеризующей уровень сложности задания, и затем уплощается, по мере того как приближается к вероятности 1,0.
Представим себе, что мы имеем одно задание (задание /) и хотим вычислить вероятность, с которой личность с данным уровнем способностей 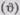 может решить это задание правильно. Уравнение для однопараметрической логистической функции будет иметь вид:
может решить это задание правильно. Уравнение для однопараметрической логистической функции будет иметь вид:
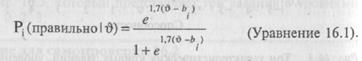
На самом деле оно не так страшно, как кажется на первый взгляд. Левая часть уравнения читается так: «вероятность того, что человек решит задание / правильно при условии, что он имеет
уровень способностей,' равный тЗ». В правой части уравнения е -это просто .число, приблизительное значение которого составляет 2,718; и — способности личности, а Ь. — это уровень трудности задания /'. В упражнении 16.1 вас просили, анализируя графики на рис. 16.3, установить вероятность того, что некто, имеющий способности, равные 1,0, может решить задание, трудность которого равна 2,0. Теперь мы можем вычислить это непосредственно с помощью логистической функции.
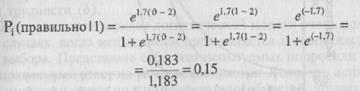
Результат согласуется с рис. 16.3. Единственное, что может создать здесь для вас некоторые проблемы, — это оценка е~''7. Это число можно вычислить с помощью калькулятора или же можно обратиться к математическим таблицам значений ех.
Важный момент, который необходимо усвоить, состоит в том, что однопараметрическая логистическая функция позволяет нам вычислить вероятность решения любого задания любым человеком при условии, что мы знаем способности этого человека и трудность задания. Трудность задания определяется положением точки на шкале способностей, которая находится на полпути вдоль ХКЗ. Поскольку в эхом случае кривые начинаются при значении, равном 0, и уплощаются при значении, равном 1, уровень трудности задания — это точка, где вероятность решения данного задания
составляет 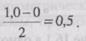
До сих пор мы полагали, что каждое задание имеет равномерное «рассеивание» по обе стороны от уровня его трудности. На самом деле это довольно жесткое допущение. Кажется весьма вероятным, что ХКЗ могут иметь различные наклоны (или уровни «дискриминации»), как показано на рис. 16.4. Малая величина дискриминации указывает на то, что индивидуумы с широким диапазоном способностей имеют обоснованные шансы ответить на задание правильно. Большая величина дискриминации говорит о том, что ХКЗ в значительно большей степени ориентирована вертикально. (Математически искушенный читатель может, вероят-
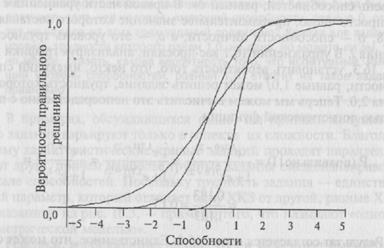
Рис. 16.4. Характеристические-кривые трех заданий.
но, рассматривать параметр дискриминации как точку перегиба на ХКЗ.)
Задание для самопроверки 16.3
Два задания на рис. 16.4 имеют уровни трудности, равные 0. Из них одно задание имеет показатель дискриминации, равный 0,5, а второе имеет показатель дискриминации, равный 1,0. Последнее задание имеет уровень трудности, равный 1,0, и показатель дискриминации, равный 2,0. Можете ли вы установить, какая из кривых связана с каждым из заданий?
Очень легко модифицировать уравнение 16.1 в однопараметри-ческое логистическое уравнение, чтобы принять в расчет второй параметр дискриминации, который обычно обозначается как а,. Модифицированная формула выглядит так:
Дата добавления: 2015-03-03; просмотров: 903;
