Эмпирические исследования инвестиционных расходов.

Рассмотренные выше теоретические модели позволили нам выделить ряд параметров, влияющих на динамику инвестиций. В частности, мы убедились в существовании отрицательной зависимости между инвестиционными расходами и ставкой процента. Однако этого недостаточно, чтобы объяснить некоторые особенности в поведении инвестиционных расходов. Теперь мы обратимся к простейшим эмпирическим моделям инвестиций, каждая из которых обладает рядом достоинства и недостатков.

Модель простого акселератора

Эмпирические исследования выявляют тесную связь между динамикой инвестиций и выпуска. Это наблюдение легло в основу модели простого акселератора. Эта модель предполагает, что оптимальный размер капитала пропорционален выпуску:

(13) K*=nY.

Подобная зависимость не следует напрямую из рассмотренной нами теоретической модели, однако можно провести аналогию между выпуском и занятостью. Напомним, что мы показали, что рост занятости приводит к увеличению оптимального размера капитала. Для некоторых производственных функций, например, для функции Кобба-Дугласа, занятость, а, следовательно, и капитал действительно пропорциональны выпуску. Следует заметить, что коэффициент пропорциональности n будет постоянен только при условии, что не изменяются издержки капитала, о которых мы говорили выше.

Записав соотношение (13) для двух разных моментов времени, находим, что чистые инвестиции пропорциональны изменению выпуска:

(14) .

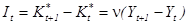Таким образом, согласно теории простого акселератора, инвестиции пропорциональны изменению выпуска.

Несмотря на то, что эта модель довольно хорошо описывает циклическое поведение инвестиций, в ней игнорируется ряд важных моментов. Во-первых, как мы уже говорили, предполагается неизменность издержек капитала, что не соответствует действительности. Во вторых, текущий уровень капитала связывается с текущим уровнем выпуска. Подобная зависимость проблематична, поскольку уровень выпуска не известен заранее. В соотношении (13) следует использовать ожидаемый выпуск, а не реальный. Модель также не принимает во внимание наличие лагов в инвестиционном процессе, связанных с производством и установкой капитальных благ.

Модель гибкого акселератора

Модель гибкого акселератора базируется на предположении о постепенной корректировке величины капитала, причем, чем больше разрыв между существующей и оптимальной величинами основного капитала, тем быстрее идет процесс инвестирования

(15) K_t = K_t-1 +l(K* - K_t-1 ), где 0< l<1

Коэффициент l показывает, какая доля разрыва между оптимальной и действительной величинами капитала будет ликвидирована в текущем периоде. Таким образом, чистые инвестиции равны:

(16) I_t=K_t- K_t-1 =l(K*-K_t-1)

Заметим, что если запас капитала равен оптимальной величине капитала

(К_t-1=К*), то чистые инвестиции равны нулю, однако это не означает, что инвестиции отсутствуют. Валовые инвестиции все равно будут положительны, поскольку нужно покрывать амортизационные расходы.

Проиллюстрируем процесс приспособления к оптимальному уровню капитала, описываемый соотношениями (15) и (16) на примере (смотри рисунок 3). Мы выбрали коэффициент приспособления l=0.5 и изобразили динамику капитала на левом рисунке и динамику чистых инвестиций – на правом рисунке.

Теория инвестиций q- Тобина

Джеймс Тобин предложил оценивать разрыв между существующей и оптимальной величинами основного капитала на основе информации, которую дает фондовый рынок. Для этого используется переменная q, которая равна отношению рыночной стоимости фирмы (согласно оценке фондового рынка) к стоимости капитала фирмы. Тобин показал, что q является хорошим индикатором функционирования фирмы и прибыльности инвестиций. Если q высок (больше единицы), то это означает, что оптимальный уровень капитала превышает существующий и, следовательно, инвестиции должны быть также велики.

Обозначим через K существующий уровень капитала фирмы, а через V – рыночную стоимость фирмы, которая равна приведенному потоку дивидендов, тогда коэффициент q можно записать, как q=V/K (будем рассматривать однопродуктовую экономику, а потому цены не фигурируют в выражении для q). Как показал Хаяши[11] (Hayashi, 1982), если производственная функция обладает постоянной отдачей от масштаба, то q также может быть подсчитано, как изменение стоимости фирмы в результате увеличения запаса капитала на единицу (то есть, среднее q равно предельному q). Учитывая это, рассмотрим предельное q, которое можно представить следующим образом.

Предположим, что запас капитала постоянен, а, значит, предельный продукт капитала также постоянен. Тогда дополнительная единица капитала увеличивает прибыль (до выплаты дивидендов) на величину, равную MPK-d, где d-норма амортизации. Приведенная стоимость потока дополнительных дивидендов равна предельному q:

.

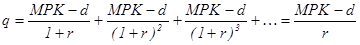Из соотношения (17) находим, что, если q больше единицы, то MPK>r+d, откуда следует, что капитал нужно увеличивать и наоборот, если q меньше единицы, то MPK<r+d, то запас капитала следует уменьшить.

Коэффициент q является индикатором прибыльности инвестиций для фирмы, но на уровне экономики в целом, как показывают эмпирические исследования, связь между q и динамикой инвестиций довольно слабая.