МОДЕЛИРОВАНИЕ НЕПРИРЫВНЫХ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЙ

1. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ

Освоение методов получения реализаций непрерывной случайной величины на ЭВМ. Имитация случайных воздействий по заданному закону на ЭВМ.

2. ОСНОВЫ ТЕОРИИ

При построении имитационных моделей часто возникает необходимость в получение реализаций разного рода случайных величин: промежутков времени между некоторыми событиями, воздействий некоторых физических величин на систему управления, размеров обрабатываемых деталей и т.п.

Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом служат обычно случайные величины, имеющие равномерное распределение в интервале [0,1].

Для получения реализаций непрерывной случайной величины X с заданной плотностью распределения вероятностей f(x) существует немало искусственных приёмов. Они достаточно полно излагаются в [2]. Из этих методов весьма распространен метод нелинейного преобразования, называемым методом обратной функции. Этот метод основан на использовании соотношения

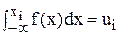, i=1,2,…

в котором u_i - i-я реализация случайной величины U, равномерно распределённой в интервале [0,1]; x_i - i-я реализация случайной величины X, описываемой плотностью вероятности f x).

При использовании интегральной функции распределения вероятностей P[x<x_i]=F(x_i) получаем уравнение

F( x_i)=u_i, i=1,2,3,...,

решение которого относительно x_i даёт явную функциональную связь между x_i и u_i: x_i=F^-1( u_i).

В некоторых случаях метод обратной функции легко алгоритмизируется и даёт явное выражение для расчёта искомой случайной величины с заданным законом распределения вероятностей.

Равномерное распределение

Для имитации равномерного распределения на интервале от a до b используют обратное преобразование соответствующей функции распределения, которое приводит к выражению

x= a + (b-a) u,

где u - случайные числа, полученные от ДСЧ.

Экспоненциальное распределение

Когда вероятность наступления события в малом интервале времени Dt очень мала и не зависит от наступления других событий, то интервалы времени между последовательными событиями распределяются по экспоненциальному закону с плотностью вероятностей

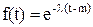, m £ t < 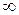, ( m=const).

Этому закону распределения подчиняются многие явления, например, длительность телефонных разговоров, срок службы многих электронных деталей, время поступления заказов на предприятие и т.д.

Для имитации экспоненциального распределения используют обратное преобразование функции плотности

T = -(l/ 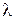) ln u + m,

где u - случайные числа, получаемые от ДСЧ.

Метод обратных функций позволяет формально записать формулы для моделирования любой случайной величины. Однако довольно часто невозможно аналитическое определение обратной функции. В подобных случаях используют специальные методы моделирования. Используют либо специальные законы теории вероятностей, либо особенности моделируемого закона распределения вероятностей. К числу подобных подходов относится и подход при моделировании нормально распределённой случайной величины.