Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

5.1 Точечные оценки

Оценка параметра называется точечной, если она выражается одним числом. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должка представлять собой случайную величину с распределением, зависящим от распределения исходной случайной величины, в том числе и от самого оцениваемого параметра, и от числа опытов n.

К точечным оценкам предъявляется ряд требований, определяющих их пригодность для описания самих параметров:

1. Оценка называется состоятельной, если при увеличении числа наблюдений она приближается (сходится по вероятности) к значению оцениваемого параметра.

2. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру.

3. Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра.

На практике не всегда удается удовлетворить одновременно все эти требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных выше точек зрения.

Получаемая в результате многократных наблюдений информация об истинном значении измеряемой величины и рассеивании результатов наблюдений состоит из ряда результатов отдельных наблюдений (ряда наблюдений) X₁; Х₂; ...; Хп, где п—число наблюдений. Их можно рассматривать как п независимых случайных величин с одним и тем же распределением, совпадающим с распределением F_х(x). Поэтому

М [Х_i] =М [X]; D [.Y_i] = D [X}; i = 1, 2, ..., п.

В этих условиях в качестве оценки истинного значения измеряемой величины естественно принять среднее арифметическое полученных результатов наблюдений:

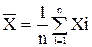
Строго говоря, среднее арифметическое представляет собой лишь оценку математического ожидания результата измерения и может стать оценкой истинного значения измеряемой величины лишь после исключения систематических погрешностей.

Будучи вычисленным на основе ограниченного числа опытов, среднее арифметическое само является случайной величиной. Математическое ожидание:

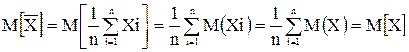
Это значит, что среднее арифметическое является несмещенной оценкой истинного значения. Однако несмещенными будут и все другие оценки вида

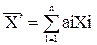
если 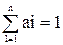. Среди всех определенных таким образом оценок среднее арифметическое имеет наименьшую дисперсию. Для этого вычислим дисперсию :

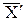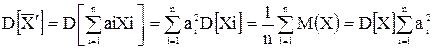
Но квадратичная форма 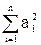,: достигает минимума, если все a_i,

одинаковы и равны 1/n. Тогда из оценки 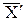мы получаем среднее арифметическое 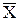, которое является поэтому эффективной оценкой с дисперсией

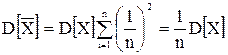
Таким образом, дисперсия среднего арифметического оказывается в п раз меньше дисперсии результатов наблюдений, или в терминах среднего квадратического отклонения:

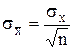
т. е. среднее квадратическое отклонение среднего арифметического в 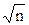раз меньше среднего квадратического отклонения результата наблюдений.

По мере увеличения числа наблюдений 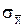стремится к нулю. Это означает, что среднее арифметическое ряда наблюдений сходится по вероятности к математическому ожиданию и является его состоятельной оценкой.

Из этого не следует, что среднее арифметическое ближе к истинному значению, чем результат каждого отдельного наблюдения. Напротив, некоторые из результатов наблюдений могут быть ближе к Q, но, к сожалению, мы не можем выбрать эти результаты из числа других результатов ряда. Именно поэтому приходится прибегать к определению среднего арифметического.

Логическим следствием оценки истинного значения измеряемой величины средним арифметическим ряда наблюдений является оценка фактических значений случайных погрешностей случайными отклонениями результатов наблюдений от среднего арифметического:

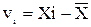
Поэтому точечную оценку дисперсии принято определять как

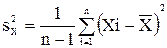
а оценку среднего квадратического отклонения результатов наблюдений как

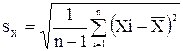
Полученные оценки позволяют записать итог измерений в виде

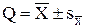
Интервал, определяемый правой частью этого равенства, с некоторой вероятностью «накрывает» истинное значение Q измеряемой величины. Однако точечные оценки ничего не говорят о значении этой вероятности.

5.2 Интервальные оценки.

Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров.

Вначале остановимся на определении доверительного интервала для среднего-арифметического значения измеряемой величины. Предположим, что распределение результатов наблюдений нормально и известна дисперсия. Тогда вероятность попадания результате наблюдений в интервал

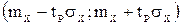
если систематические погрешности исключены (m_X =Q),

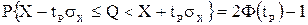
Это означает, что истинное значение Q измеряемой величины с доверительной вероятностью 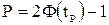находится между границами доверительного интервала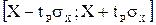

Половина длины доверительного интервала 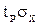называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р= 0,95 или Р = 0,995, и по формуле

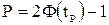
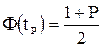
определяют соответствующее значение 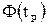интегральной функции нормированного нормального распределения. Затем по таблицам находят значение коэффициента t_p и вычисляют доверительное отклонение .

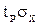Проведение многократных наблюдений позволяет значительно сократить доверительный интервал. Действительно, если результаты наблюдений X, (i = 1, 2, ..., п) распределены нормально, т.е. нормально распределены и величины—X_i, а значит и среднее арифметическое X, являющееся их суммой. Поэтому имеет место равенство

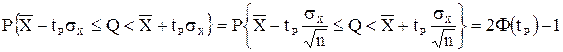
где t_p определяется по-прежнему по заданной доверительной вероятности Р.

Полученный доверительный интервал, построенный с помощью среднего арифметического результатов п независимых повторных наблюдений, в 1/n раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.

Половина длины нового доверительного интервала

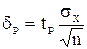
называется доверительной границей погрешности результата измерений, а итог измерений записывается в виде:

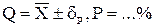
Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих условиях пользуются отношением называемым дробью Стьюдента.

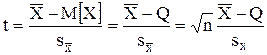
Входящие в нее величины 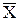и S_x вычисляют на основании опытных данных, они представляют собой точечные оценки математического ожидания и среднего квадратического отклонения результатов наблюдений.

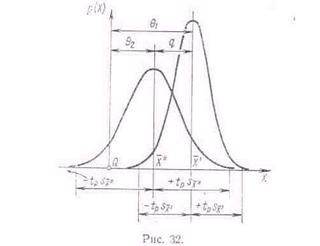
Плотность распределения этой дроби, впервые предсказанного В. С. Госсетом, писавшим под псевдонимом Стьюдент, и впоследствии доказанного Р. А. Фишером, который связал его с именем Стьюдента, выражается следующим уравнением:

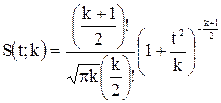
где 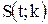— плотность распределения Стьюдента. Величина k называется числом степеней свободы и равна п— 1.

Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале 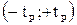вычисляется по формуле:

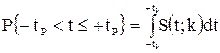
или поскольку 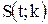является четной функцией, то:

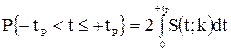
подставив в выражение вероятности значение дроби Стьюдента получим:

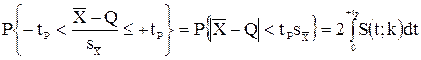
Величины t_P протабулированы для значений P=0,10…0,99 и k=1…30.

Отклонение

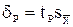
называется доверительной границей погрешности результата измерений, а итог измерений записывается в виде:

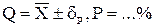
5.3Точечные оценки истинного значения измеряемой величины и среднего квадратического отклонения на основании ограниченного ряда наблюдений

Мы подошли к решению вопроса о том, как на основании полученной в эксперименте группы результатов паблюдьнкй оценить истинное значение, т. е. найти результат измерений, и как зценить его точность.

Эта задача является частным случаем статистической задачи нахождения оценок, параметров функции распределения случайной величины на основании выборки—ряда значений, принимаемых этой величиной в п независимых опытах.

Оценку а параметра а назовем точечной, если она выражается одним числом. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должка представлять собой случайную величину с распределением, зависящим от распределения исходной случайной величины, в том числе и от самого оцениваемого параметра, и от числа опытов п.

К точечным оценкам предъявляется ряд требований, определяющих их пригодность для описания самих параметров.

2. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру.

3. Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра.

Получаемая в результате многократных наблюдений информация об истинном значении измеряемой величины и рассеивании результатов наблюдений состоит из ряда результатов отдельных наблюдений (ряда наблюдений) Xi; Х^, ...; Хп, где п—число наблюдений. Их можно рассматривать как п независимых случайных величин с одним и тем же распределением, совпадающим с распределением F^(x). Поэтому

М [Х,] =М [X]; D [.Y,] = D [X}; i = 1, 2, ..., п.

Будучи вычисленным на основе ограниченного числа опытов, среднее арифметическое само является случайной величиной. .

Дисперсия среднего арифметического оказывается в п раз меньше дисперсии результатов наблюдений, или в терминах среднего квадратического отклонения:

Среднее квадратическое отклонение среднего арифметического в n раз меньше среднего квадратического отклонения результата наблюдений. Это означает, что среднее арифметическое ряда наблюдений сходится по вероятности к математическому ожиданию п является его состоятельной оценкой.

Из этого, конечно, отнюдь не следует, что среднее арифметическое ближе к истинному значению, чем результат каждого отдельного наблюдения. Напротив, некоторые из результатов наблюдений могут быть ближе к Q, но, к сожалению, мы не можем вы-боать эти результаты из числа других результатов ояда. Именно

поэтому приходится прибегать к определению среднего арифметического.

На рис. 24 представлен график, на котором точками, соединенными пунктирными линиями, обозначены результаты ряда измерений ускорения свободного падения, полученные во ВНИИМ. На том же рисунке точками, соединенными сплошной линией, изображены средние арифметические для двух, трех и так далее до пятнадцати результатов последовательных наблюдений. Среднее из пятнадцати наблюдений -9,81923 м-с-², т. е. ордината последней точки служит оценкой истинного значения ускорения свободного падения.

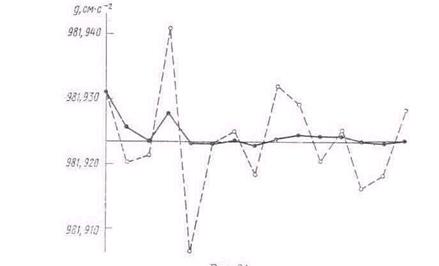
Из графика видно, что если результаты отдельных наблюдений значительно разбросаны относительно среднего арифметического, то разброс отдельных средних арифметических значительно меньше и быстро уменьшается по мере увеличения числа наблюдений. Интересно отметить, что результат шестого по счету наблюдения совпадает с окончательным средним арифметическим, но узнать об этом мы смогли только после обработки всего ряда наблюдений. Поэтому шестой результат имеет такую же познавательную ценность, как четвертый или пятый, наиболее удаленные от среднего арифметического ряда.

v,=X,-X

Но мере увеличения числа наблюдений распределение случайных отклонений результатов наблюдений асимптотически сходится : распределению случайных погрешностей.

Эта оценка характеризует сходимость результатов отдельных наблюдений, т. е. степень их концентрации относительно среднего арифметического. Последнее, являясь случайной величиной, имеет дисперсию, в п раз меньшую дисперсии случайной погрешности.

5.4 Оценка с помощью интервалов

Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями

(доверительными) находятся истинные значения оцениваемых параметров.

Вначале остановимся на определении доверительного интервала для среднего-арифметического значения измеряемой величины. Предположим, что распределение результатов наблюдений нормально и известна дисперсия ст²^ . Тогда, полагая в уравненик (VI.34) /I = —/а = tp, найдем вероятность попадания результате наблюдений в интервал (mx—tpax; m^+tpax). Согласно формулам (VI.38) и (VI.39)

Р [тх — tpax < -Y< mx + tp^x} =

= Ф (tp) - ф (- tp) == 2 Ф (tp) - 1. Но

P {mx—tpax<.X^mx -}- tpax} =

= P[X - tp^x<mx<X -i- tpax} и, если систематические погрешности исключены (тд- == Q),

. Р {Х - tpr.x < Q < К + tpax} == 2Ф (tp) - 1. (VI. 49»

Это означает, что истинное значение Q измеряемой величины с доверительной вероятностью Р= 2Ф {tp) — 1 находится между границами доверительного интервала [X— 1р<зх',Х 4- tpax\.

Половина длины доверительного интервала tpffx называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р= 0,95 или Р = 0,995, и по формуле

2Ф {tp) - 1 = Р;

Ф(^)=и^ (VI. 50;

определяют соответствующее значение Ф(^) интегральной функции нормированного нормального распределения. Затем по данны-.'-табл. 7 Приложения находят значение коэффициента tp и вычисляют доверительное отклонение tpox.

нормально распределены и величины—X,, а значит и среднее п

арифметическое X, являющееся их суммой. Поэтому имеет место равенство

P[x-tpo-^Q<^x+tp^}= =Pb-tp^_^Q<7(+ tp ^и=2Ф(^)-1, (VI. 51)

( у л v ri\

гце tp определяется по-прежнему формулой по 'заданной доверительной вероятности Р.

Полученный доверительный интервал, построенный с помощью среднего арифметического результатов п независимых повторных наблюдений, в1/га раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.

Половина длины нового доверительного интервала

8р==/р^- ' (VI. 52) Уп

называется доверительной границей погрешности результата из-мгрений, а итог измерений записывается в виде

Q=^±5p; P= ... %. (VI. 53)

Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих усло-зиях пользуются отношением

^ Х-М[Х] ^X^Q^^X^Q^ ^54) ^ ^ ^

называемым дробью Стыодента. Входящие в нее величины А' и Sx вычисляют на основании опытных данных; они представляют собой точечные оценки математического ожидания [см. формулу (VI.40)] и среднего квадратического отклонения результатов наблюдений [см. формулу (VI.46)].

Плотность распределения этой дроби, впервые предсказанного В. С. Госсетом, писавшим под псевдонимом Стьюдент, и впоследствии доказанного Р. А. Фишером, который связал его с именем Стыодента, выражается следующим уравнением:

fk—1\> _*_¹

^'^f¹^) ^s- ⁽^VL⁵⁵⁾

где 5 (i;; k) — плотность распределения Стьюдента. Величина k называется числом степеней свободы и равна п— 1.

Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале (—tp; +'tp\, согласно выражению (VI.17), вычисляется по формуле

Р \— tp < t < + tp} = J ^р S {(; k) at,

нием отклонений результатов наблюдений от среднего значения явно обнаруживается. Если бы случайные погрешности были невелики, то значения неисправленных отклонений меняли бы свой знак при некотором среднем значении измеряемой величины. Случайные погрешности несколько искажают эту картину, однако если они даже одного порядка малости с систематическими погрешностями, в последовательности знаков можно заметить некоторую неравномерность: неисправленные отклонения результатов одного знака чаще встречаются в одной половине ряда, чем в другой. В рассматриваемом случае последовательность знаков имеет- вид

В первой половине последовательности знак плюс встречается пять раз, а во второй только два раза, в то время как знак минус встречается чаще во второй половине ряда.

Если же в ряде результатов наблюдений присутствует периодическая систематическая погрешность, то группы знаков плюс и минус в последовательности неисправленных отклонений результатов наблюдений могут периодически сменять друг друга, если. конечно, случайные погрешности не особенно велики.

Обобщая два рассмотренных случая, можно сказать: если знаки неисправленных отклонений результатов наблюдений чередуются правильно, то данный ряд результатов наблюдений обнаруживает прогрессивную погрешность, если последовательность знаков плюс сменяется последовательностью знаков минус или наоборот, и периодическую погрешность, если группы знаков плюс и минус чередуются.

По этому признаку можно обнаружить ситематические погрешности, если случайные погрешности малы. Однако даже при достаточно больших случайных погрешностях анализ графиков неисправленных отклонений результатов наблюдений позволяет обнаружить весьма слабые тенденции к той или иной форме систематического изменения погрешности. Так, например, рассматривая рис. 30, легко заметить прогрессивную погрешность, составляющую приблизительно 0,8 мкм на длине 4 мм, хотя разброс случайных погрешностей значительно больше (1,5—1,6 мкм)-

5.5 Введение поправок

Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерения. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдений, которые позволяют оценить степень рассеивания ое-

^: Для исправления результатов наблюдений их складывают " с поправками, равными систематическим погрешностям по вели-^\ чине и обратными им по знаку. Поправки определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью. Для исправления результата наблюдения его складывают только со средним аоифметическим значением поправки:

X,=X\+q, (VI 1.6)

где Xi; Х'г — соответственно исправленный и неисправленный результаты наблюдений; q — среднее арифметическое значение поправки.

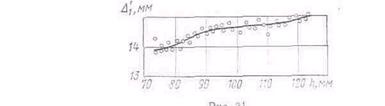
Поправки, определяемые экспериментально, задаются в виде таблицы или графика. Так, например, на рис. 31 представлена зависимость поправки на депрессию ртути в однокапиллярном образцовом компрессионном манометре ВНИИМ от высоты подъема ртути. График был получен путем многократных наблюдений при давлении ^ог^^Па путем сравнения положений мениска з капилляре и в широкой трубке, депрессия ртути в которой принималась равной нулю.

Поправка на депрессию меняется с высотой подъема ртути з пределах 13,94—14,90 мм. Среднее квадратическое отклонение результата определения поправки, вычисленное по отклонениям отдельных экспериментальных значений от плавной кривой, составляет при этом 0,16 мм.

Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая.

Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок (иногда несколько десятков). При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.

Действительно, при исправлении неисправленного результата Х'г путем введения поправок iJ^Sj, /= 1, 2,...; :;о формуле

х,-^.-^,

дисперсия s²^- становится равной

s^s² ⁺ S s², (VI 1.7) х х • ^ i

где s²^' —оценка дисперсии неисправленных результатов; s²,— оценка дисперсии ]'-и поправки.

Следовательно, где-то должна быть разумная граница тех значений поправок, которые следует вводить в результаты наблюдений для получения более достоверных сведений об истинном значении измеряемой величины.

Поправку имеет смысл вводить до тех пор, пока она уменьшает доверительные границы погрешности.

Это означает, что целесообразно вводить поправку, если она больше половины доверительной погрешности ее определения.

При исчезающе малой дисперсии поправки может показаться, что введение любой поправки повышает достоверность результата. Однако следует помнить, что погрешность результата выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц разряда, следующего за последним десятичным знаком погрешности результата, будет все равно потеряна при округлении, и вводить ее не имеет смысла.

<7 8 91011 12 13 >

Дата добавления: 2015-01-24; просмотров: 1833;