ИМИТАЦИЯ ПОТОКОВ СОБЫТИЙ

1. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ

Освоение методов моделирования потоков событий. Имитация потока входных заявок в системах массового обслуживания.

2. ОСНОВЫ ТЕОРИИ

Потоком событий называют последовательность однородных событий, появляющихся одно за другим в случайные моменты времени. Примеры: поток вызовов на телефонной станции; поток забитых шайб при игре в хоккей; поток автомобилей на АЗС; поток заявок на предприятиях бытового обслуживания и т.п. Имитацию потоков событий наиболее часто приходится проводить при исследовании систем массового обслуживания.

С потоком событий можно связывать различные случайные события, но не имеет смысла говорить о вероятностях "событий", образующих поток.

Поток событий случаен, поэтому вычислить можно только какую-то его конкретную реализацию.

Поток событий наглядно изображается рядом точек с абсциссами t₁,t₂,...,t_j,...(например, последовательностью моментов времени, в которые в систему поступают заявки). При вероятностном описании поток событий может быть представлен последовательностью случайных величин-промежутков времени между последовательными событиями:

Z₁=t₁;

Z₂=t₂-t₁;

Z₃=t₃-t₂;

...... ;

Z_j=t_j-t_j-1.

...... .

Тогда последовательность случайных величин представляется следующим образом: t₁, t₂=t₁+Z₂, t₃=t₂+Z₃ и т.д.

В общем случае для задания последовательности случайных величин Z_m (m=1,2,3,... ) требуется указать совместные функции распределения

F(x₁,x₂,...,x_m) = P[Z₁<x₁,...,Z_m<x_m].

Такое описание очень громоздко, в связи с чем на практике используются частные типы потоков событий, допускающие более простое описание.

Наиболее часто используются стационарные потоки с ограниченным последствием. Для этих потоков вероятность попадания того или другого числа событий на любой интервал времени зависит только от длины этого интервала и не зависит от расположения интервала на оси времени, а сами интервалы Z_j - независимые случайные величины с одинаковой плотностью расрпеделения f_j(x)=f(x) ( i=2,3,...).Плотность распределения f₁(x)-момента поступления t₁ первой заявки может отличается от f(x) и связана с ней формулой

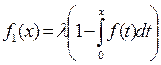
где λ - интенсивность потока событий.

Способ моделирования стационарного потока с ограниченным последствием достаточно прост. Сначала получают реализацию случайной величины с плотностью f(x) и находят момент времени появления первого события – t₁. Далее последовательно осуществляется следующая процедура. Пусть t_j-момент наступления j-го события уже вычислен. Получаем реализацию Z случайной величины с плотностью распределения вероятностей f(x) и вычисляем момент t_j+1 прихода очередного события: t_j+1=t_j+Z и т.д.

Рассмотрим конкретные, часто используемые, типы потоков и способы их имитации.