Поток Эрланга порядка k
Потоком Эрланга k-го порядка называют поток событий, получающегося "прореживанием" простейшего потока, когда сохраняется каждая k-я точка (событие) в потоке, а все промежуточные выбрасываются.
Интервал времени между двумя соседними событиями в потоке Эрланга k-го порядка представляет собой сумму k независимых случайных величин Z1,Z2,...,Zk, имеющих показательное распределение с параметром λ:
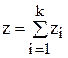

Закон распределения случайной величины Z называется законом Эрланга k-го порядка и имеет плотность
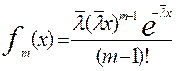 , (x > 0).
, (x > 0).
Математическое ожидание и дисперсия случайной величины Z соответственно равны:
M[Z]=k/ 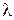 ; D[Z]=k/
; D[Z]=k/ 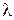 2.
2.
На основе определения потока Эрланга получается простой способ моделирования: прореживается пуассоновский поток с интенсивностью  =
= 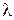 /k, т.е. в пуассоновском потоке допускаем моменты времени с номерами 1,2,...,k-1, а k-й момент оставляем, т.к. он принадлежит новому потоку и т.д. Таким образом, моменты времени потока Эрланга вычисляются по формулам:
/k, т.е. в пуассоновском потоке допускаем моменты времени с номерами 1,2,...,k-1, а k-й момент оставляем, т.к. он принадлежит новому потоку и т.д. Таким образом, моменты времени потока Эрланга вычисляются по формулам:
t1 = 0;
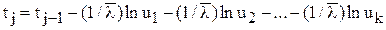 , j=1,2,3,...,
, j=1,2,3,...,
где 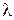 - интенсивность потока Эрланга k-го порядка, uj - случайные числа от ДСЧ.
- интенсивность потока Эрланга k-го порядка, uj - случайные числа от ДСЧ.
3. ОБЪЕКТЫ И СРЕДСТВА ИССЛЕДОВАНИЯ
Объектами исследования в лабораторной работе являются потоки событий, образованные слиянием нескольких потоков с известными характеристиками.
В процессе имитации потоков событий используются различные методы сортировки.
Одним из простых методов сортировки является метод пузырька (BUBBLE) который позволяет массив A, содержащий N элементов, расположить, например, в возрастающем порядке. Соответствующий алгоритм приведен на рис.4.1. Однако. Более эффективным методом для данного типа задач будет метод вставки.
процедура BUBBLE(A, N);
N1=N-1;
Цикл I=1,N1;
begin
K=1;
10 J=K+1;
Если A(K) £ A(J) то идти к 20;
U=A(K);
A(K)=A(J);
A(J)=U;
K=K-1;
Если (K³1), то идти к 10;
20 end;
Конец
Рис.4.1. Подпрограмма сортировки методом пузырька
В лабораторной работе могут быть использованы и другие более эффективные методы сортировки (например, адресная сортировка и т.п.).
4. ПОДГОТОВКА К РАБОТЕ
4.1. Ознакомиться с основными типами потоков событий.
4.2. Ознакомиться с методами моделирования пуассоновского, равномерного потока событий и потока Эрланга порядка k.
4.3. Ознакомиться с методами сортировки массивов чисел.
5. ПРОГРАММА РАБОТЫ
В некоторую систему массового обслуживания по различным каналам поступают заявки, образующие поток событий заданного типа. На входе системы потоки сливаются в один. Составить алгоритм и программу имитации результирующего потока, указанного в варианте.
Первые 100 моментов времени поступления заявок в результирующем потоке вывести на печать. По первым 1000 заявкам рассчитать оценку средней интенсивности потока. Найденную оценку сравнить с теоретическим значением интенсивности потока.
5.1. Поток образован слиянием трёх пуассоновских потоков событий с интенсивностями 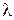 1,
1, 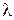 2,
2, 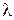 3 (1/с) ( табл.5.1. ).
3 (1/с) ( табл.5.1. ).
Таблица 5.1.
| Вариант | ||||||
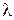 1 1
| 2,5 | 1,5 | ||||
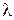 2 2
| 0,5 | |||||
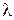 3 3
| 0,5 | 0,5 | 0,5 |
5.2. Поток образован слиянием двух равномерных потоков с параметрами a1, b1 и a2, b2 ( с ) ( табл. 5.2. ).
Таблица 5.2.
| Вариант | ||||||
| a1 | 1,5 | |||||
| b1 | 2,5 | 1,5 | ||||
| a2 | 0,5 | |||||
| b2 |
5.3. Поток образован слиянием пуассоновского потока с интенсивностью 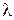 (1 /с ) и равномерного потока с параметрами a и b ( с ) ( табл.5 3. ).
(1 /с ) и равномерного потока с параметрами a и b ( с ) ( табл.5 3. ).
Таблица 5.3.
| Вариант | ||||||
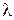
| 0,5 | 0,5 | ||||
| а | 0,5 | 0,5 | ||||
| b | 1,5 |
5.4. Результирующий поток является потоком Эрланга k-го порядка с интенсивностью 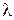 ( 1/с ) ( табл.5.4. ).
( 1/с ) ( табл.5.4. ).
Таблица 5.4.
| Вариант | ||||||
| K | ||||||
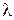
| 0,5 | 0,5 | 0,5 |
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Дать определение потока событий.
6.2. Как строится вероятностное описание потока событий.
6.3. В чём состоит способ моделирования стационарного потока с ограниченным последствием.
6.4. Охарактеризовать пуассоновский поток и способ его моделирования.
6.5. Охарактеризовать равномерный поток и способ его моделирования.
6.6. Дать характеристику потока Эрланга k-го порядка и метода его имитации.
6.7. Привести характеристики потока событий, исследованного в лабораторной работе.
Дата добавления: 2015-02-19; просмотров: 3006;
