ОБРАБОТКА РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ
1. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ
Исследование достоверности и точности имитационного моделирования. Практическое освоение методов обработки результатов машинных экспериментов с моделями систем.
2. ОСНОВЫ ТЕОРИИ
В общем случае имитационное моделирование всегда проводится с целью определения некоторых оценок показателя (или показателей) эффективности системы. Проводить имитационное моделирование целесообразно лишь в случаях, когда интересующий исследователя показатель эффективности системы невозможно или сложно определить аналитически. Процесс моделирования требует, как правило, больших затрат машинного времени или весьма быстродействующую вычислительную технику. Кроме того, имитационное моделирование-это своего рода искусственный эксперимент с цифровой моделью системы. Обработка результатов эксперимента принципиально не может дать точных значений показателя эффективности системы, в лучшем случае можно построить хорошую оценку такого показателя. При этом неизбежно возникают вопросы точности и достоверности оценки показателя эффективности. Проделав большое количество опытов (прогонов) с моделью системы, получают экспериментальный материал, который для получения искомых оценок обрабатывается далее методами математической статистики. Рассмотрим процедуры обработки для наиболее распространенных типов критерия эффективности.
Оценка неизвестной вероятности
Допустим, что цель моделирования состоит в оценки вероятности p какого-либо события A, связанного с работой системы. Событие A например, может обозначать возникновение аварийной ситуации в системе, отказ элементов системы и др.
В результате прогонов модели выясняется, произошло ли событие A или нет. Пусть за N прогонов модели событие A зафиксировано в M прогонах. Оценкой неизвестной вероятности 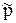 = P[A] служит в этом случае частота
= P[A] служит в этом случае частота
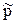 = M/N
= M/N
Эта частота и является оценкой искомого критерия эффективности 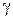 . Различают абсолютную точность ε критерия интерпретации (показателя эффективности)
. Различают абсолютную точность ε критерия интерпретации (показателя эффективности) 
Различают абсолютную точность ε критерия интерпретации (показателя эффективности) 
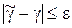 ,
,
и относительную
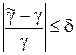 .
.
Они связаны простым соотношением: 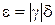
Так как левые части приведённых неравенств случайны по своей природе, то для однозначного определения качества моделирования вводится понятие достоверности. Достоверность модели 1- 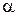 (надёжность, доверительная вероятность) есть вероятность того, что результаты моделирования удовлетворяют заданной точности:
(надёжность, доверительная вероятность) есть вероятность того, что результаты моделирования удовлетворяют заданной точности:

Обычно α - малое число: 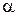 = 0,05 или
= 0,05 или 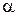 = 0,01. Это соотношение и используется для определения количества испытаний N такого чтобы оценка
= 0,01. Это соотношение и используется для определения количества испытаний N такого чтобы оценка 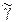 не превышала истинного значения с заданной точностью
не превышала истинного значения с заданной точностью 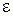 при заданной доверительной вероятности 1-
при заданной доверительной вероятности 1- 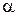 .
.
Решение задачи основывается на том факте, что оценка 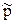 является не смещённой (M[
является не смещённой (M[ 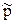 ] = p) и асимптотически нормальной, т.е. нормированная случайная величина
] = p) и асимптотически нормальной, т.е. нормированная случайная величина
( 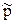 - p)/
- p)/ 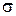 p* , (
p* , ( 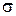 p =
p = 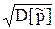 ).
).
при больших N имеет распределение, близкое к нормальному:
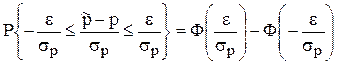
где 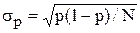 - среднеквадратическое отклонение
- среднеквадратическое отклонение 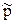 :
:
Ф(x)-интеграл вероятностей :
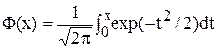
Приравнивая разность интервалов вероятностей к заданной доверительной вероятности, получим уравнение
2Ф( 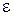 /
/ 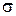 p ) = 1-
p ) = 1- 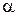 ,
,
корнем которого является число tα, называемое квантилем нормального распределения. Тогда для достижения заданной доверительной вероятности должно выполняться соотношение
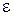 /
/ 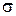 p = tα.
p = tα.
Заменяя в нём 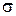 p на
p на 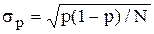 , получим формулу, определяющую требуемое число прогонов модели N:
, получим формулу, определяющую требуемое число прогонов модели N:
N = tα2[p(1-p)/ 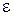 2] .
2] .
В формулу входит неизвестная вероятность p, которую определяют следующим образом.
1. Так как p(1-p)£1/4, то можно пользоваться усиленной оценкой
N³(ta2/4 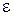 2)
2)
2. Производят некоторое количество прогонов модели N1 и по ним получают оценку 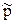 1=M1/N1, которую потом используют для оценки N:
1=M1/N1, которую потом используют для оценки N:
N ³tα2[ 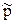 1(1-
1(1- 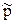 1)/
1)/ 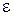 2] .
2] .
Процедуру можно повторить несколько раз. На рис. 5.1 приведена схема алгоритма соответствующих вычислений, в которой обозначено: N - номер очередного прогона; M - число появлений события A; p - оценка вероятности события A; NK - номер контрольного прогона, на котором делается проверка точности; L - число прогонов между контрольными; NN - ограничение максимального количества прогонов.
Вычисления по приведённой схеме заканчиваются либо при достижении заданной точности, либо при достижении максимального числа прогонов. В последнем случае величина 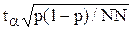 показывает отклонение случайной оценки от p.
показывает отклонение случайной оценки от p.
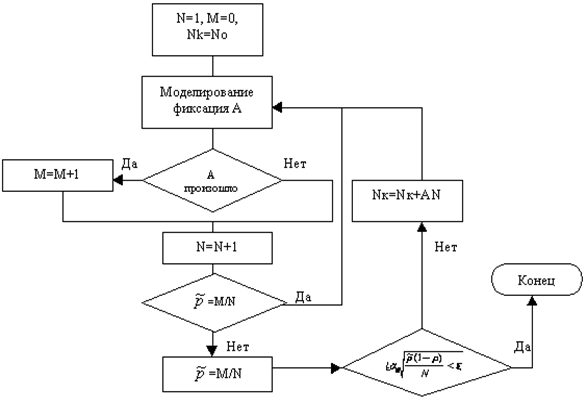
Рис. 5.1. Схема алгоритма получения оценки 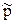 с ипользованием контрольных прогонов.
с ипользованием контрольных прогонов.
Оценка среднего значения критерия
Допустим, что показатель эффективности системы представляет собой случайную величину X, а целью моделирования является оценка M[X] - математического ожидания показателя. При каждом прогоне равенство модели фиксируется одно значение показателя эффективности; за N прогонов получается выборка X1,X2,...,XN.. В качестве оценки M[X] берут в этом случае выборочное среднее
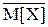 = (1/N)(X1+X2+...+XN)
= (1/N)(X1+X2+...+XN)
Оценка M[X] также асимптотически нормальная и, следовательно, неравенство
| 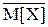 -M[X]|£
-M[X]|£ 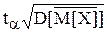
имеет место с вероятностью не меньшей, чем 1-α. Под корнем стоит дисперсия оценки 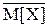 :
:
D( 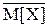 ) = D[X]/N
) = D[X]/N
Чтобы обеспечить заданную точность ε, необходимо взять N таким, чтобы имело место
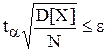
Неизвестную дисперсию D[X] в этом соотношение заменяют при вычислении её оценкой
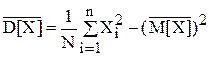
На рис. 5.2 приведена схема вычислений. В ней использован хорошо известный приём накопления суммы значений X и суммы квадратов этих значений: после каждого прогона вычисляется
S1 = S1+Xi,
S2 = S2+Xi2.
В начале S1=S2=0. Нужные нам величины просто выражаются через S1 и S2:
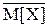 =S1/N
=S1/N
D[X]=(S2/N)-(S1/N)2.
Контроль точности ведётся через L прогонов.
Начало
1. N = 0, NK = 1;
2. S1 = 0, S2 = 0;
3. N = N+1 ;
4. Если N>NN то идти к 11
5. Прогон модели. Фиксация X;
6. S1 = S1+X, S2 = S2+X ;
7.Если N£ NK идти к 3
8. M =S1/N, D=S2/N-M2
9. 
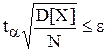
10. NK=NK+L
11. Печать M, D, N.
Конец
Рис. 5.2. Схема алгоритма оценивания среднего значения показателя эффективности системы
Оценка p - квантиля распределения
Пусть в процессе моделирования некоторой системы подсчитывается значение показателя эффективности X, который предполагается случайной величиной. Если функцию распределения обозначить F(x), то p - квантилем распределения F(x) называют число xp, являющееся решением системы
F(xp)=p,
Значение этой характеристики случайной величины состоит в том, что P[X<xp]=p, т.е. с вероятностью p значения X не превосходит p - квантиля xp.
Рассмотрим простой способ оценки квантиля.
Полученные в результате N прогонов модели значения X1,X2,...,XN упорядочиваются по возрастанию. Обозначим упорядоченные значения через Xi*. Тогда
X1* , X2* ,..., XN*.
В этой последовательности из N чисел находим число, номер которого равен: Целое (Np). Если, например, N=1000, а p=0,95, то целое (Np) = 950. Это и принимаем за оценку p - квантиля. Таким образом, Xp = X*[Np].
3. ОБЪЕКТЫ И СРЕДСТВА ИССЛЕДОВАНИЯ
Объектами исследования в данной лабораторной работе являются модели широко распространённых явлений и процессов в практике человека: отражение радиолокационных сигналов от объекта, взвешивание тел на аналитических весах, передачи сигналов по каналам с помехами.
Оценка искомых числовых характеристик, указанных в задании на лабораторную работу, производится на ЭВМ методом имитационного моделирования с использованием универсального языка программирования.
4. ПОДГОТОВКА К РАБОТЕ
4.1. Ознакомиться с основными типами распределений случайных величин и методами их моделирования на ЭВМ.
4.2. Подготовить и иметь в распоряжении датчик случайных чисел с равномерным законом распределения, написанный на выбранном языке моделирования.
4.3. Ознакомиться с методами оценивания эффективности системы.
5. ПРОГРАММА РАБОТЫ
5.1. В лабораторной работе вычисляется характеристика модели некоторого процесса, указанной вариантом задания. В соответствие с заданием составить алгоритм, программу для ЭВМ и оценить с точностью ε=0,01 и доверительной вероятностью 0,95 одну из следующих характеристик:
1. Вероятность события X>K.
2. Математическое ожидание X.
3. Математическое ожидание X2.
4. 0,95 - квантиль распределения X.
5.2. Для одной из следующих моделей вычислить указанную в п. 5.1 характеристику.
Модель 1.
Начинается строительство нового предприятия. Предварительные расчеты показали, что прибыль предприятия будет сильно зависеть от эксплуатационных расходов, емкости рынка и доли предприятия на рынке. Для оценки возможной доли предприятия с достаточной точностью можно использовать экспоненциальный закон распределения случайной величины X (доли предприятия в общей массе конкурентов):
f(x) = (1/K)exp(-x/K),
где K – средняя доля предприятия.
Модель 2.
При пуске нового предприятия истинные эксплуатационные расходы остаются пока неизвестными. Оценка возможных эксплуатационных расходов осуществлялась в предположении о нормальном законе их распределения с параметрами: математическое ожидание К и среднеквадратическим отклонением 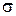 =10-1К
=10-1К
Модель 3.
Тело взвешивается на аналитических весах. Истинное, неизвестное нам значение веса тела равно К. Вследствие наличия ошибок результат каждого взвешивания X случаен и распределен по нормальному закону с параметрами К и средне квадратическим отклонением 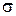 =10-2К.
=10-2К.
Модель 4.
По информационному каналу передаются сообщения. Во время их передачи в канале наблюдаются импульсивные помехи. Интервал времени между начальными моментами появления помех является случайной величиной X, распределённой по закону, описываемому гамма - распределением с параметрами 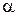 =10/К,
=10/К, 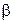 =10/К2.
=10/К2.
5.3. Конкретный вариант задания определяется номером модели и номером оцениваемой величины.
Список вариантов: 1.1, 1.2, 1.3, 1.4, 2.1, 2.2, 2.3, 2.4, 3.1, 3.2, 3.3, 3.4.
4.1, 4.2, 4.3, 4.4.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Что такое критерий эффективности системы?
6.2. Почему говорят об оценки показателя эффективности, а не о его точном значение?
6.3. Что такое точность и достоверность показателя эффективности?
6.4. Какую интерпретацию может иметь показатель эффективности?
6.5. Какие понятия математической статистики лежат в основе получения оценки показателя эффективности системы?
6.6. Каким образом определяется необходимое число машинных прогонов модели для достижения заданной точности и достоверности оценки показателя эффективности ?
6.7. Что такое квантиль распределения и как он оценивается?
6.8. Дать интерпретацию результатов имитационных экспериментов с моделями, исследуемыми в лабораторной работе.
Дата добавления: 2015-02-19; просмотров: 1732;
