Нормальное распределение

Нормальное, или гауссово распределение - один из наиболее важных и часто используемых видов распределения.

Все известные методы генерирования нормально распределенных случайных чисел основаны на преобразовании Z=(X-a)/ 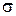, где a - математическое ожидание, 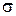-среднеквадратическое отклонение. В этом случае случайная величина Z распределена нормально с математическим ожиданием равным 0 и среднеквадратическим отклонением равным 1 (её называют стандартной случайной величиной, описываемой плотностью распределения

Переход к требуемому нормальному распределению осуществляется соотношением X=a+Z ).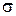

Достаточно эффективным подходом к моделированию стандартной нормально распределённой случайной величины является алгоритм Марсальи-Брея, быстро дающий точные результаты. По этому алгоритму генерируются два случайных числа u₁ и u₂. Далее полагая V₁=-1+2u₁ и V₂=-1+2u₂, вычисляют S=V₁²+V₁². При S³1 начинают цикл снова.

При S<1 вычисляются

.

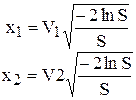Для генерирования 100 пар нормально распределённых случайных чисел понадобится в среднем 127 пар случайных чисел ( U₁ и U₂).

Алгоритм генерирования стандартных нормальных случайных величин приведен на рис.3.1. Алгоритм может быть оформлен в виде процедуры с формальными параметрами (EX, SKO, X1, X2).

процедура NORMAL (EX,SKO,X1,X2)

1 V1=2*RANDОM - 1

V2=2*RANDOM - 1

S=V1*V1+V2*V2

Если (S ³ 1.0) идти к 1

SQ=SQRT(-2*ALOG(S))/S)

R1=V1*SQ

R2=V2*SQ

X1=EX+R1*SKO

X2=EX+R2*SKO

Возврат в точку вызова

Конец

Рис.3.1. Программа генератора нормально распределённых случайных величин

Исходными данными здесь являются математическое ожидание EX и среднеквадратическое отклонение SKO. За одно обращение к программе получаются два нормально распределённых случайных числа X1 и X2.

Логарифмически-нормальное распределение

Случайная величина X имеет логарифмически-нормальное распределение, если величина Y= ln(X-A) распределена по нормальному закону. Величина A является параметром этого закона распределения вместе с параметрами a и σ нормального закона для Y. Плотность распределения случайной величины X задаётся формулой

.

Математическое ожидание и дисперсия определяются по формулам

M[X]=A+exp( 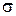²/2 + a), D[X] = (exp( 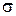²)-1) exp( 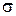²+2a).

Используя связь X и Y, получаем следующий способ имитации логарифмически - нормально распределённой случайной величины X:

1) имитируется стандартная нормальная величина Y;

2) вычисляется X=A + exp(Y).

Гамма-распределение

Гамма-распределение является одним из наиболее полезных видов непрерывных распределений в имитационном моделировании. Если величины, характеризующие какое-либо случайное явление, не могут принимать отрицательных значений, то, скорее всего, такое явление наиболее удачно может имитироваться с помощью гамма - распределения.

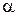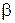Это распределение описывается двумя параметрами, и , где 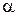характеризует форму, а 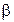-масштаб распределения ( рис.3.2).

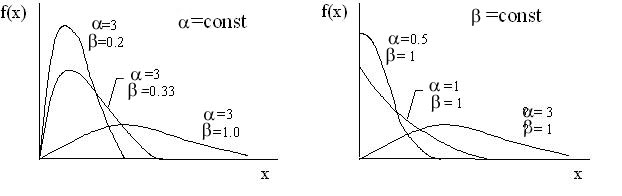
Рис. 3.2. Гамма-распределение.

При изменении этих параметров плотность гамма-распределения -

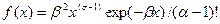
где 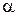>0, 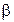=0 X>0, математическое ожидание M[X]= 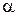/ 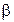дисперсия D[X]= 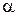/ 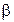², может принимать самую различную форму, что делает его одним из наиболее универсальных видов распределений для построения различных видов моделей.

На рис.3.3 показан алгоритм достаточно удобного двухпараметрического гамма - генератора Филлипса [1] GAMMA с формальными параметрами (ALPHA, BETA, START, X).

Значения ALPHA, BETA и начальное значение START (целое число менее 1,5) являются исходными данными.

Для определения значений параметров гамма - распределения можно воспользоваться уравнением

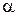=M²[X]/D[X]; 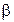=M[X]/D[X].

Гамма-распределение связано с целым рядом других полезных распределений. Например, есл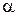и =1 и 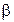=const, то генерируется экспоненциальная функция плотности. Если α принимает целочисленное значение K, то получим распределение Эрланга-К. Если 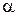=v/2 и 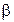=2 ( где v -число степеней свободы), получается распределение хи-квадрат. Могут быть получены и другие виды распределений.

Процедура GAMMA (ALPHA,BETA,START,X);

Если (START³1.5) идти к 60;

X3=1.0;

Если (ALPHA£1.5) идти к 1;

Если (ALPHA£19.0) идти к 2;

Идти к 3;

1 B=0.24797+(1.34735740*ALPHA)-(0.00004204*ALPHA**2)+

(0.53203176*ALPHA**3)-(0.13671536*ALPHA**4)+(0.01320864*ALPHA**3);

Идти к 4;

2 B=0.64350+(0.45839602*ALPHA)-(0.02952801*ALPHA**2)+(0.00172718

*ALPHA**3)-(0.00005810*ALPHA**4)+(0.00000082*ALPHA**5);

идти к 4;

3 B=1.33408+(0.22499991*ALPHA)-(0.00230695*ALPHA**2)+

(0.00001623*ALPHA**3)-(0.00000006*ALPHA**4);

4 Y=1.0+(1.0/B);

START=5.0;

12 Если (Y-1.0 <0) то 110;

Если (Y-1=0), то 50;

15 Y=Y-1.0;

X3=X3*Y;

Идти к 12

110 GY=1.0+Y(-0.5771017+Y*(0.985854+Y*(-0.8764218+Y*

(0.8328212+Y*(-0.5684729+Y*(0.2548205+Y*(-0.05143930)))))));

X3=X3*GY/Y;

50 A=(X3/(ALPHA*BETA))**B;

B=1.0/B;

A=1.0/A;

60 X=(-A*ALOG(URAND(IX)))**B;

Возврат в точку вызова

Конец.

Рис.3.3. Алгоритм генератора для случайных величин, подчиняющихся гамма - распределению с параметрами ALPHA и BETA ( X-случайная величина, имеющая гамма-распределение).

3. ОБЪЕКТЫ И СРЕДСТВА ИССЛЕДОВАНИЯ

Объектами исследования в лабораторной работе являются программные генераторы случайных величин, распределённых по заданному закону.

Исследование генераторов и использование их для имитации случайных воздействий проводится с помощью ПЭВМ.

Используемый язык программирования – любой универсальный.

4. ПОДГОТОВКА К РАБОТЕ

4.1. Ознакомится с методами получения реализаций случайных величин с заданным законом распределения вероятностей.

4.2. Ознакомится с генераторами случайных величин, распределённых по равномерному, экспоненциальному, нормальному, логарифмически-нормальному и гамма законам.

4.3. Повторить выбранный для работы язык программирования.

5. ПРОГРАММА РАБОТЫ

5.1. Составить схему алгоритма и программу для имитации случайной величины X, распределённой по заданному закону.

Варианты законов распределения случайной величины X:

1) равномерное распределение;

2) экспоненциальное распределение;

3) нормальное распределение;

4) логарифмически-нормальное распределение;

5) гамма-распределение.

Параметры законов распределения могут быть выбраны произвольно. Программу оформить в виде стандартной подпрограммы.

5.2. Составить схему алгоритма и написать программу вычисления вероятности события

M[X]-1/k£X£M[X]+1/k,

где k-номер студента по списку группы, X-случайная величина с заданными в п.5.1 законами распределения. При составлении программы рекомендуется использовать написанную в соответствие с п.5.1 подпрограмму для вычисления значения X. Используя 10000 реализаций X, вывести на печать 30 первых значений случайной величины, гистограмму распределения и значение частоты попадания в указанный выше интервал. Сравнить эту частоту с теоретической вероятностью.

6.КОНТРОЛЬНЫЕ ВОПРОСЫ

6.1. Какие методы используются для формирования значений случайной величины с заданным языком распределения?

6.2. В чём состоит сущность метода обратной функции?

6.3. Привести алгоритм имитации равномерного и экспоненциального распределений.

6.4. Изложить алгоритмы имитации случайной величины по нормальному и логарифмически-нормальному законам распределения.

6.5. Чем объясняется разница между теоретической вероятностью и частотой попадания исследуемой в лабораторной работе величины X в заданный интервал её значений?