Задача 2. Оптимальное распределение заказа между фирмами
Методические указания к проведению
практических занятий для студентов специальности
280103 Защита в чрезвычайных ситуациях
Составители : Шаптала Владимир Григорьевич
Шаптала Виталий Владимирович
Радоуцкий Владимир Юрьевич
Подписано в печать Формат 60х84/16. Усл. печ. Уч.-изд. л. 6,5
Тираж 57 экз. Заказ Цена
Отпечатано в Белгородском государственном технологическом университете
им. В.Г. Шухова
308012, г. Белгород, ул. Костюкова, 46.
Задача 1. Графическое решение матричных игр.
1. Найдем оптимальные стратегии игроков в игре, заданной платежной матрицей
.
Сначала проверим, есть ли в данной игре седловая точка.
Нижняя цена игры равна 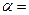 max {4, 3} = 4.
max {4, 3} = 4.
Верхняя цена этой игры равна 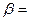 min {7, 9, 9, 9} = 7.
min {7, 9, 9, 9} = 7.
Поскольку 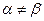 , то седловой точки у данной игры нет, и решение нужно искать в смешанных стратегиях.
, то седловой точки у данной игры нет, и решение нужно искать в смешанных стратегиях.
Графически решаются те матричные игры, в которых хотя бы у одного из игроков есть лишь две чистые стратегии. Задача именно этого игрока и решается графически. В задаче 1 у первого игрока две чистых стратегии, а у второго − четыре, поэтому будем решать графически задачу первого игрока.
Смешанная стратегия первого игрока задается вектором 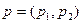 . Построения осуществляются следующим образом. На горизонтальной прямой откладывается отрезок единичной длины, характеризующий вероятность применения чистых стратегий первым игроком. Каждой точке этого отрезка сопоставляется смешанная стратегия первого игрока по следующему правилу: расстояние от точки до правого конца отрезка задает величину
. Построения осуществляются следующим образом. На горизонтальной прямой откладывается отрезок единичной длины, характеризующий вероятность применения чистых стратегий первым игроком. Каждой точке этого отрезка сопоставляется смешанная стратегия первого игрока по следующему правилу: расстояние от точки до правого конца отрезка задает величину 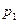 , а расстояние до левого его конца − величину
, а расстояние до левого его конца − величину 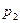 (см. рисунок 1.1). Для определенных таким образом величин
(см. рисунок 1.1). Для определенных таким образом величин 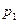 и
и 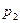 выполняются соотношения
выполняются соотношения 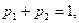
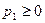 ,
, 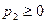 , поэтому, согласно (5), вектор
, поэтому, согласно (5), вектор 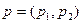 задает смешанные стратегии первого игрока.
задает смешанные стратегии первого игрока.
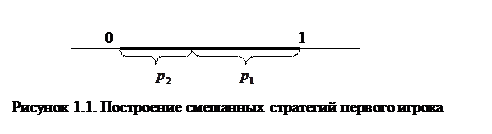
Тогда точка 0 задает вектор (1, 0), т. е. первую чистую стратегию первого игрока, а точка 1 задает вектор (0, 1), т. е. вторую чистую стратегию первого игрока. Далее через концы единичного отрезка проводятся вертикальные линии. На этих линиях откладываются выигрыши первого игрока при применении вторым игроком его различных чистых стратегий. При этом выигрыши в случае применения первым игроком его первой чистой стратегии располагаются на левой вертикальной линии, а соответствующие второй чистой стратегии первого игрока − на правой вертикали. Точки левой и правой вертикали, соответствующие одной и той же чистой стратегии второго игрока, соединяются отрезками.

На рисунке 1.2 изображены выигрыши первого игрока при применении вторым игроком первой чистой стратегии. Римскими цифрами указано, что второй игрок применяет именно первую чистую стратегию.
Любая точка K этого отрезка с координатами 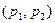 и
и 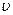 показывает, что если первый игрок будет применять свою смешанную стратегию
показывает, что если первый игрок будет применять свою смешанную стратегию 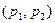 , а второй игрок − свою первую чистую стратегию, то средний выигрыш первого игрока будет равен
, а второй игрок − свою первую чистую стратегию, то средний выигрыш первого игрока будет равен 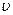 .
.
Аналогичные построения выполняются для остальных чистых стратегий второго игрока (рисунок 1.3). Римские цифры указывают на номер его чистой стратегии.

Жирным шрифтом выделена ломаная, соответствующая нижней границе выигрыша первого игрока, т.е. дающая его средний гарантированный выигрыш. В точке М находится наибольший гарантированный выигрыш первого игрока (так как М − наивысшая точка ломаной). Эта точка является пересечением отрезков, соответствующих первой и второй чистым стратегиям второго игрока. Эти стратегии называются активными. Второй игрок будет использовать их в своей оптимальной смешанной стратегии с ненулевой вероятностью. Отрезки, соответствующие третьей и четвертой чистым стратегиям второго игрока, не проходят через точку М, поэтому эти стратегии в оптимальную смешанную стратегию второго игрока войдут с нулевыми вероятностями, так как их реализация приведет к большему проигрышу второго игрока. Такие стратегии называют пассивными.
При определении оптимальной смешанной стратегии первого игрока и цены игры используется следующее утверждение:
Утверждение 1.Если один из игроков применяет свою оптимальную смешанную стратегию, то его выигрыш будет равен цене игры, независимо от того, с какими вероятностями применяет другой игрок свои активные стратегии.
Выпишем соотношения для нахождения оптимальной смешанной стратегии первого игрока, основываясь на утверждении 1. В нашем примере платежная функция, согласно (7), имеет вид:
Пусть оптимальная смешанная стратегия первого игрока равна 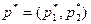 . По утверждению 1 он получит выигрыш, равный цене игры
. По утверждению 1 он получит выигрыш, равный цене игры 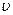 , с какими бы вероятностями не применял второй игрок свои активные стратегии. Мы рассмотрим случаи, когда второй игрок применяет свои активные чистые стратегии, т.е. либо первую, либо вторую.
, с какими бы вероятностями не применял второй игрок свои активные стратегии. Мы рассмотрим случаи, когда второй игрок применяет свои активные чистые стратегии, т.е. либо первую, либо вторую.
Итак, пусть 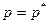 ,
, 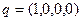 . Тогда
. Тогда 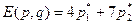 .
.
Пусть 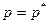 ,
, 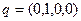 . Тогда
. Тогда 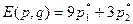 . Приравняем эти значения к цене игры
. Приравняем эти значения к цене игры 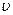 и добавим уравнение
и добавим уравнение 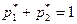 , получим систему уравнений:
, получим систему уравнений:
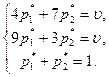 (9)
(9)
Решив эту систему, получаем 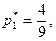
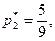
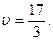
Теперь найдем оптимальную смешанную стратегию второго игрока. Пусть она задается вектором 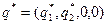 . Здесь мы учли тот факт, что третья и четвертая чистые стратегии второго игрока являются пассивными. Выпишем величину проигрыша второго игрока, если он применяет свою оптимальную смешанную стратегию, а первый игрок − свои чистые стратегии.
. Здесь мы учли тот факт, что третья и четвертая чистые стратегии второго игрока являются пассивными. Выпишем величину проигрыша второго игрока, если он применяет свою оптимальную смешанную стратегию, а первый игрок − свои чистые стратегии.
Пусть 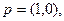
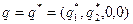 . Тогда
. Тогда 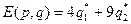 .
.
Пусть 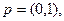
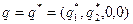 . Тогда
. Тогда 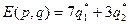 .
.
Применяем утверждение 1, учитывая, что цена игры найдена и равна 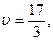 получим систему уравнений:
получим систему уравнений:
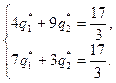
Решив эту систему, получаем 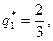
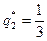 . Итак, оптимальная смешанная стратегия второго игрока задается вектором
. Итак, оптимальная смешанная стратегия второго игрока задается вектором 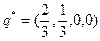 .
.
Ответ к данной задаче запишем в виде:
|
2. Рассмотрим теперь матричную игру, платежная матрица которой является транспонированной к матрице задачи 1, т.е. игра задается матрицей
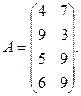
В новой игре первый игрок имеет четыре чистые стратегии, а второй − две. Нижняя цена игры 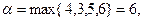 а верхняя цена игры
а верхняя цена игры 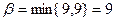 .
.
Так как 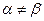 , то у этой игры нет седловой точки, поэтому нужно искать ее решение в смешанных стратегиях. Пусть
, то у этой игры нет седловой точки, поэтому нужно искать ее решение в смешанных стратегиях. Пусть 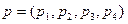 − вектор смешанных стратегий первого игрока, а
− вектор смешанных стратегий первого игрока, а 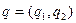 − вектор смешанных стратегий второго игрока. Платежная функция данной игры равна:
− вектор смешанных стратегий второго игрока. Платежная функция данной игры равна:
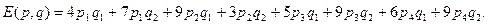
Второй игрок имеет две чистые стратегии, поэтому графически будет решаться задача второго игрока. Построения выполняются аналогично п.1, если поменять местами первого и второго игроков (см. рисунок 1.4). Цель второго игрока, согласно его осторожному поведению, состоит в минимизации его возможного риска. Риск второго игрока (т.е. максимально возможный проигрыш второго игрока при применении им той или иной смешанной стратегии) на рисунке 1.4 показан жирной линией. Точка M обозначает минимальный риск второго игрока. Она лежит на пересечении отрезков, соответствующих второй и четвертой чистым стратегиям первого игрока.

Обозначим оптимальную смешанную стратегию второго игрока 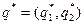 . Для нахождения значений
. Для нахождения значений 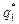 и
и 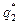 воспользуемся утверждением 3. Активными стратегиями первого игрока являются вторая и четвертая. Тогда
воспользуемся утверждением 3. Активными стратегиями первого игрока являются вторая и четвертая. Тогда
1) 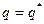 ,
,  =>
=> 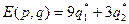 .
.
2) 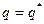 ,
, 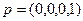 =>
=> 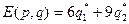 .
.
Приравняем эти значения к цене игры 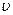 и добавим уравнение
и добавим уравнение 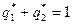 , получим систему уравнений:
, получим систему уравнений:
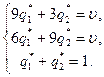
Решив эту систему, получаем 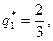
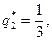
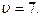
Теперь найдем оптимальную смешанную стратегию первого игрока, 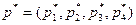 . Так как его активные стратегии − вторая и четвертая, а первая и третья пассивные, то
. Так как его активные стратегии − вторая и четвертая, а первая и третья пассивные, то 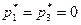 . Следовательно,
. Следовательно, 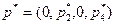 . Применяя утверждение 1 и учитывая, что цена игры уже найдена, получим систему уравнений:
. Применяя утверждение 1 и учитывая, что цена игры уже найдена, получим систему уравнений:
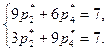
Решая эту систему, получаем 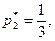
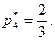
Итак, решение матричной игры задается векторами 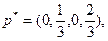
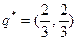 и ценой игры
и ценой игры 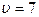 :
:
|
Задача 2. Оптимальное распределение заказа между фирмами
Предприниматель должен принять решение о приобретении d единиц продук-ции, которую выпускают две фирмы. Известно, что если он закажет первой фирме х изделий, то ему придется заплатить ей
f1(x) = a0 + a1x + a2x2 (руб.),
а при выполнении этого заказа второй фирмой его затраты составят
f2(x) = b0 + b1x + b2x2 (руб.).
Нужно найти оптимальное распределение заказа между фирмами, при котором общие затраты будут минимальными, а также определить максимальный уровень затрат, соответствующий самому неудачному решению предпринимателя.
Исходные значения параметров представлены в таблице:
| d | a0 | a1 | a2 | b0 | b1 | b2 |
| 0.2 | 0.3 |
Требуется:
1) составить математическую модель оптимального распределения заказа между фирмами;
2) найти графическим методом распределения заказа с минимальными и макси-мальными затратами;
3) определить оптимальное распределение заказа методом множителей Лагранжа; дать экономическую интерпретацию множителю Лагранжа.
Дата добавления: 2015-02-05; просмотров: 1777;

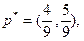

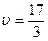 .
.
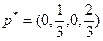 ,
, 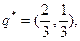
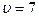 .
.