СЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ЧИСЕЛ

2. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ

Изучение функционирования программных датчиков псевдослучайных чисел. Практическая проверка качества генераторов случайных чисел.

2. ОСНОВЫ ТЕОРИИ.

При построении стохастических имитационных моделей необходимо обеспечить возможность генерирования случайных величин. Для этой цели используются случайные числа, равномерно распределённые в интервале [0,1]. Естественно, что, если имитационная модель просчитывается на ЭВМ, необходимо:

1) получить равномерно распределённые случайные числа;

2) использовать эти случайные числа для генерации случайных величин с требуемыми характеристиками.

Следует заметить, что получить на ЭВМ случайное число, равномерно распределённые в интервале [0,1], строго говоря, в принципе невозможно из-за конечной разрядности любой ЭВМ. Однако отличие получаемых реализаций случайной величины от реализации величины равномерно распределённой оказывается незначительным для ЭВМ с высокой разрядностью.

Методы получения на ЭВМ значений случайной величины, равномерно распределённой в интервале [0,1], можно разделить на три большие группы:

1. Использование физических датчиков (генераторов) случайных чисел.

2. Использование таблиц случайных чисел.

3. Получение псевдослучайных чисел.

Первая группа методов основана на использовании специальных устройств, сопрягаемых с ЭВМ и являющихся источником собственно случайности. В качестве таких устройств могут использоваться генераторы шума, источники радиоактивного излучения и т.д. С помощью подобных устройств разрядная сетка машин заполняется набором независимых значений случайных двоичных чисел.

Вторая группа методов получения случайных чисел на ЭВМ связана с использованием таблиц случайных чисел. Подобные таблицы составляются с помощью специальных технических устройств - "электронных рулеток" и могут иметь очень большой объём.

Основной недостаток использования таблиц случайных чисел при статическом моделировании на ЭВМ - большая загрузка памяти вычислительной машины. В оперативной памяти такие таблицы обычно не располагаются ввиду их слишком большого объёма, а размещение их на внешних накопителях существенно снижает быстродействие ЭВМ. Поэтому таблицы случайных чисел очень редко используются при моделировании на ЭВМ.

Третья группа методов получения псевдослучайных чисел основана на использовании специальных алгоритмов генерации псевдослучайных последовательностей чисел. Подобные алгоритмы имеют рекуррентную структуру и жёстко детерминированы. Задав начальные значения последовательности, мы однозначно определим все её элементы. Однако полученный на выходе генератора массив чисел можно в принципе рассматривать как совокупность реализаций случайной величены. Именно поэтому последовательности, полученные с помощью таких алгоритмов, называют псевдослучайными и обращаются с ними как с массивами реализаций случайной величены, используя для их анализа все методы математической статистики.

Объём массива чисел псевдослучайной последовательности всегда ограничен. В любой ЭВМ с конечной разрядностью N число возможных значений величины, лежащей в интервале [0,1], составляет 2^N-1 (один разряд знаковый). Следовательно, в последовательности чисел R_n рано или поздно появится такое число R_L (L £ 2^N-1), которое уже там было. Начиная с этого числа, все предыдущие числа последовательности начнут повторяться.

Таким образом, массив получаемых чисел псевдослучайной последовательности ограничен величиной L - отрезком апериодичности. Длина отрезка апериодичности зависит от метода генерации чисел и от типа ЭВМ, на которой этот генератор реализуется.

К настоящему времени разработано довольно много генераторов псевдослучайных чисел. Рассмотрим некоторые наиболее известные из них.

Мультипликативный конгруэнтный метод. Метод представляет собой арифметическую процедуру для генерирования конечной последовательности равномерно распределённых чисел. Основная формула метода имеет вид:

X_i+1=aX_i(mod m),

где a и m - неотрицательные целые числа. Согласно этому выражению, мы должны взять последнее случайное число X_i, умножить его на постоянный коэффициэнт a и взять модуль полученного числа по m ( т.е. разделить на aX_i и остаток считать как X_i+1 ). Поэтому для генерирования последовательности чисел X_i необходимы начальное значение X₀, множитель a и модуль m. Эти параметры выбирают так, чтобы обеспечить максимальный период и минимальную корреляцию между генерируемыми числами.

Правильный выбор модуля не зависит от системы счисления, используемой в данной ЭВМ. Для ЭВМ, где применяется двоичная система счисления, m=2^N ( N-число двоичных цифр в машинном слове ). Тогда максимальный период (который получается при правильном выборе a и X₀ )

L=2^N-2=m/4, (N>2) .

Выбор a и X₀ зависит также от типа ЭВМ. Для двоичной машины

a=8T±3;

где T может быть любым целым положительным числом, а X₀-любым положительным, но нечётным числом. Следует заметить, что указанный выбор констант упрощает и ускоряет вычисления, но не обеспечивает получения периода максимальной длины. Больший период можно получить, если взять m, равное наибольшему простому числу, которое меньше чем 2^N, и a, равное корню из m. Максимальная длина последовательности будет увеличена от m/4 до m-1 ( метод Хатчинсона). Изложенный алгоритм, записанный на псевдокоде, представлен в приложении. Имя подпрограммы-RANDU.

Подпрограмма RANDU (RANDOM) имеется в математическом обеспечении многих ЭВМ (в том числе и РС). При этом константы, используемые в подпрограмме, для 32-разрядного машинного слова имеют значения a=5¹³=1220703125, i/m=0,4656613E-9.

Смешанные конгруэнтные методы. На основе конгруэнтной формулы были созданы и испытаны десятки генераторов псевдослучайных чисел. Работа этих генераторов основана на использовании формулы

X_i+1=aX_i+C(mod m),

где a, c, m- константы, обычно автоматически вычисляемые в подпрограмме. На основе этого алгоритма разработана процедура URAND, которая приведена в приложении 1.1. Грин, Смит и Клем предложили аддитивный конгруэнтный метод. н основан на использовании рекуррентной формулы

X_i+1=(X_i+X_i-1)(mod m).

При X₀=0 и X₁=1 этот приводит к особому случаю, называемому последовательностью Фибоначчи.

Другие алгоритмы основаны на комбинации двух генераторов с перемешиванием получаемых последовательностей.

Поскольку при использовании детерминированных алгоритмов получаемая последовательность чисел является псевдослучайной, возникает вопрос: насколько они близки по своему поведению случайным? Для ответа на него предложено великое множество самых разнообразных методов статических испытаний. Среди наиболее часто используемых тестов можно указать следующие:

1. Частотные тесты. Используют либо критерий хи-квадрат, либо критерий Колмогорова-Смирнова для сравнения близости распределения полученного набора чисел к равномерному распределению.

2. Сериальный тест. Фиксирует частоты появления всех возможных комбинаций чисел 2,3,4,...и проводит оценку полученных данных по критерию хи-квадрат.

3. Интервальный тест. Проводит подсчёт знаков, появляющихся между повторами каких-либо цифр и сравнивает с ожидаемым по критерию хи-квадрат.

4. Спектральный тест. На основе применения анализа Фурье изменяет статистическую независимость соседних групп чисел. Характеризуется как наиболее чувствительный тест.

Следует заметить, что при любом конечном наборе критериев последовательность, которая пройдёт все статистические испытания, может оказаться всё же совершенно неприемлемой для некоторых приложений. Поэтому на практике лучше подбирать генератор, пользуясь простыми тестами (типа первых трёх). Использование критерия хи-квадрат для оценки близости полученного с помощью генератора распределения чисел к равномерному сводиться к следующим действиям.

Весь диапазон чисел [0,1] разбивается на k интервалов. Статистика 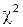определяется выражением

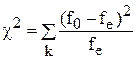
где f₀-наблюдаемая частота для каждого интервала; f_e-ожидаемая частота для каждого интервала ( f_e=p*N, N-число опытов ).

Если 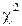=0, то наблюдаемые и теоретически предсказанные значения частот точно совпадают. Если 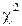>0, то расчётные значения сравниваются с табличными значениями 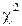_T. Значения 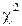_T табулированы для различных чисел степеней свободы v=r-1-m, где r-число интервалов, m-число параметров распределения, определяемых из опыта, и уровней доверительной вероятности 1-a. Если расчётная величина 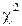оказывается больше табличной, то между наблюдаемым и теоретическим распределением имеется значительное расхождение.

3. ОБЪЕКТЫ И СРЕДСТВА ИССЛЕДОВАНИЯ

Объектами исследования в лабораторной работе являются два генератора случайных чисел (термин "псевдослучайность" редко используется при практическом моделировании). Алгоритмы реализации генераторов приведены в приложении. В дальнейшем будем называть их датчиками случайных чисел.

Первый датчик, построенный на основе смешанного конгруэнтного метода, реализован как подпрограмма (функция) URAND (см. рис. П1). Для получения случайных чисел следует использовать обращение URAND(IX), где IX-любое целое число (при первом обращении к подпрограмме можно положить IX=0); URAND-равномерно распределённое на интервале [0,1] число.

Второй датчик, построенный на основе мультипликативного конгруэнтного метода, реализован в виде алгоритма RANDU (см. рис. П2). Для получения случайных чисел следует использовать обращение RANDU(IX,IY,U), где IX, IY-текушие случайные целые числа; U-случайное число с плавающей точкой. Перед первым обращением к подпрограмме обычно ставится оператор IX=748965373. При использовании встроенной в математическое обеспечение ЭВМ функции RANDOM отсутствие параметров обеспечивает генерацию действительных случайных чисел в диапазоне [0..1], а при заданных параметрах в диапазоне [а..в]. Все вычисления проводятся на ЭВМ с 32-разрядным словом с использованием универсального языка программирования (Фортран, Паскаль, Си и т.п.) ( Типичные средства – ПЭВМ с 32 разрядной FAT).

4. ПОДГОТОВКА К РАБОТЕ

4.1. Ознакомится с методами генерации псевдослучайных чисел.

4.2. Ознакомится с методами проверки качества датчиков случайных чисел. Обратить внимание на использование критерия хи - квадрат.

4.3. Изучить работу программных датчиков случайных чисел, приведённых в приложении.

4.4. Повторить основные конструкции и операторы используемого языка программирования и методы работы в среде автоматизации программирования.

5. ПРОГРАММА РАБОТЫ

В работе используются два рассмотренных в разделе 3 датчика случайных чисел, равномерно распределённых на интервале [(0,1]. (Возможно использование одного датчика). Генерируется N случайных чисел для последующего анализа каждого датчика. При этом весь интервал [0,1] разбивается на К меньших интервалов одинаковой длины. Найти, как случайные числа, полученные от каждого датчика, распределяются по этим К интервалам, используя при этом вывод результатов на печать в виде гистограммы распределения. Оценить близость полученных распределений к равномерному в интервале [0,1] с использованием критерия хи-квадрат.

Задание выполняется поэтапно.

5.1. Нарисовать схему алгоритма вычисления распределения случайных чисел по К интервалам.

Замечание. Самый быстрый метод, чтобы определить к какому классу относится число х, заключается в вычислении целой переменной J, соответствующей номеру класса, в который попадает данное число. Например, для интервала [(0,1], разделённого на 20 классов длиной 0.05, можно получить значение J следующим образом:

J=целое(20*x)+1.

Таким образом, чтобы подсчитать число элементов в каждом классе, можно действовать следующим образом:

1) получить от датчика случайное число x;

2) вычислить J, например, с помощью инструкции J=INT(20*x)+1;

3) установить T(J)=T(J)+1, где T-массив из К элементов и каждый элемент T(J) служит счётчиком для класса J (1≤J≤K, K=20). В начале T(J)=0.

5.2. Используя предыдущую схему, нарисовать полную схему алгоритма проверки качества датчиков случайных чисел. Включить в неё операции автоматической оценки близости полученного распределения к равномерному с использованием критерия хи-квадрат, а также операции вывода на печать номера К и соответствующего ему элемента T(J) и гистограммы распределения.

Замечание. При выборе масштаба L можно поступить следующим образом. Если одна позиция в строке соответствует L числам, то T(j) числам в классе J соответствует длина М, которая вычисляется по следующей инструкции:

М=INT(T(J)/RL+0,5),

где RL=FLOAT(L)-вычисляется только один раз перед входом в цикл, а константа 0,5 используется для округления.

5.3. Написать полную программу проверки качества датчиков случайных чисел на алгоритмическом языке и выполнить её на ЭВМ.

В качестве исходных данных принять: N=10000 чисел для каждого датчика случайных чисел, К-20.

5.4. На основе результатов расчётов сделать заключение о близости полученных распределений от двух датчиков случайных чисел к равномерному и выбрать датчик для дальнейшего использования.

6. КОНТРОЛЬНЫЕ ВОПРОСЫ.

6.1. Какие существуют способы получения случайных чисел?

6.2. Что такое псевдослучайные числа?

6.3. В чём заключается сущность мультипликативного конгруэнтного метода формирования последовательности равномерно распределённых случайных чисел?

6.4. В чём состоят особенности смешанных конгруэнтных методов генерации псевдослучайных чисел?

6.5. Какие тесты используются для проверки генераторов случайных чисел? Объяснить метод, основанный на использовании критерия хи-квадрат?

6.6. Сравнить между содой два изученных датчика случайных чисел. Отметить преимущества и недостатки каждого из них.