СТОИМОСТЬ ДЕНЕГ ВО ВРЕМЕНИ.СЛОЖНЫЙ ПРОЦЕНТ И ДИСКОНТИРОВАНИЕ

Осуществление любых инвестиционных проектов предполагает разрыв во времени между затратами и доходами. В этом случае возникает необходи­мость расчета стоимости денег во времени. Расчет стоимости денег во времени — это принцип, согласно которому до тех пор, пока существуют альтернативные возможности получения дохода, их стоимость во времени зависит от стоимости в тот момент, когда ожидается их получение. Финан­совая теория утверждает, что будущие деньги всегда дешевле сегодняш­них, и не только из-за инфляции. Деньги, которыми мы располагаем сего­дня, могут быть вложены в дело и принести доход, и, если мы получаем их через год, мы упускаем эту возможность.

Сравним сегодняшние 10 тыс. грн. с 10 тыс. грн., которые будут по­лучены через год. Если ставка банковского процента составляет 10% го­довых, то сегодняшние 10 тыс. грн. вырастут до 11 тыс. грн. через год. Следовательно, будущая стоимость сегодняшних 10 тыс. грн. составит 11 тыс. грн.:

Х = 10 тыс. грн. + 0,1 х 10 тыс.грн.

Х=11тыс.грн.

Теперь поставим вопрос несколько иначе: сколько стоят 10 тыс. грн., которые будут получены через год, при условии, что ставка банковского процента равна 10% годовых? (Такие вопросы представляют интерес для всех инвесторов.) Очевидно, их сегодняшняя, т. е. текущая, стоимость рав­на той сумме, которую следовало бы в настоящее время положить в банк, с тем чтобы она через год выросла до 10 тыс. грн. Предположим, что это какая-нибудь сумма Х. Следовательно:

X+0,1*X=10 тыс. грн.

1,1Х=10тыс. грн.

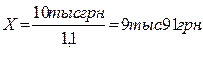
Таким образом, текущая стоимость 10 тыс. грн., которые будут полу­чены через год, составляет 9 тыс. 91 грн. Текущую стоимость называют еще приведенной стоимостью, которая, как мы видим, не измеряет стои­мость текущей суммы в какой-то момент в будущем, а позволяет опреде­лить, сколько будущая сумма стоит сегодня. Используя технику расчета приведенной стоимости, можно подсчитать сегодняшнюю стоимость той суммы, которая будет получена в будущем. Так изменяется стоимость денег во времени. •

Теперь рассмотрим концепцию будущейстоимостидля более общего случая.

Какова будущая стоимость сегодняшних инвестиций К через п лет, если годовая ставка банковского процента составляет г% ?

Через 1 год: К1=К0+К0*r =К0(\+r).

Через 2 года: К2 = К1 + К1*r= К1 (1+r) = К0(1 + r)² .

Через З года: К3=K2 +2*r=K(1+r)=K0(1+r)³. И т. д.

Чтобы определить будущую стоимость инвестиций в объеме К0 кконцу года, рассмотренную процедуру необходимо повторить п раз. Сле­довательно, будущая стоимость Kn сегодняшних капиталовложений К0 составит:

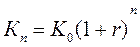
Общепринятой в финансовом анализе базовой формулой будущей стоимости является следующая:

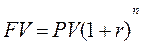
где FV — будущая стоимость;

РV — текущая стоимость;

п — число лет;

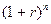— коэффициент будущей стоимости.

Из рассмотренного примера видно, что при расчете будущей стоимости определенной суммы денег используется сложный процент. Сложный про­цент — это начисление "процентов на проценты". Проценты, начисленные по истечении определенного периода (например, года), добавляются к ос­новной сумме и включаются в ту сумму, на которую в следующий период будут начисляться проценты.

Очевидно, что, чем выше ставкапроцента и чем больше срок начисле­ния процентов, тем выше будущая стоимость (FV).

Дж. М. Кейнс называл сложные проценты магией. А один из Ротшиль­дов провозгласил их восьмым чудом света. Такое отношение к сложному проценту не случайно. В начале прошлого века английский астроном Фрэнсис Бэйли подсчитал, что британский пенс, инвестированный под 5% годовых при условии начисления сложных процентов в год рождения Хри­ста, принес бы к 1810 г, столько дохода, что его хватило бы для заполнения 357 млн. земных шаров. Бенджамин Франклин был более практичным.

После своей смерти в 1790 г. он оставил по 1000 фунтов двум городам — Бостону и Филадельфии с условием, что они не будут тратить эти деньги в течение 100 лет. Наследство Бостона, эквивалентное примерно 4600 долл., к 1890 г. увеличилось до 332 000 долл.

Поскольку процесс начисления сложного процента можетбыть доста­точно утомительным, существуют таблицы факторов наращения. Полный комплект этих таблиц имеется во всех учебниках по финансовому анализу и инвестиционному проектированию. Мы приведем здесь лишь фрагмент такой таблицы. Факторы наращения в таблице показывают сумму, до кото­рой возрос бы первоначальный вклад при различных комбинациях перио­дов и процентных ставок. Например, определенная сумма, положенная на депозит, по которому выплачиваются 8%, и оставленная на нем на 2 года, возросла бы в 1,166 раза. Это значит, что если сумма депозита составляет 1000 грн., то ее стоимость через 2 года будет равна 1166 грн.

Таблица 1