Концепція та методичний інструментарій оцінки вартості грошей в часі.

Ключову роль в розрахунках, пов'язаних з потоками грошових кошті» в різні періоди, відіграє оцінка вартості грошей в часі. Концепція такої оцінки ґрунтується на тому, що вартість грошей з часом змінюється з урахуванням норми прибутку на грошовому ринку, в якості якої виступає норма позичкового процента (або процента). В даному випадку під процентом мають на увазі суми доходів під використання коштів па грошовому ринку.

Враховуючи, що інвестування є, як правило, довготривалим процесом, в інвестиційній практиці часто доводиться порівнювати вартість грошей на початку їх інвестування з їх вартістю під час повернення у вигляді майбутнього прибутку, амортизаційних відрахувань тощо.

Для цього порівняння використовують два поняття — майбутня вартість грошей та їх теперішня вартість.

Майбутня вартість грошей — це сума, в яку перетворяться інвестовані в певний момент кошти через визначений період з урахуванням визначеної ставки процента. Встановлення майбутньої вартості грошей пов'язане з її зростанням — поетапним збільшенням суми вкладу. Вона розраховується за так званою процентною ставкою, яка є одночасно вимірювачем ступеня прибутковості інвестиційних операцій.

Теперішня вартість грошей — це сума майбутніх грошових надходжень, наведених з урахуванням визначеної ставки процента (так званої «дисконтної ставки») дотеперішнього періоду. Визначення теперішньої вартості грошей пов'язане з дисконтуванням цієї вартості, що є операцією, зворотною зростанню, якщо обумовлений остаточний розмір грошових коштів. В цьому випадку сума процента (дисконту) віднімається під остаточної суми (майбутньої вартості) коштів. Така ситуацій виникає, якщо необхідно визначити, скільки коштів треба інвестувати сьогодні для того, щоб через визначений період одержати заздалегідь встановлену суму.

Виконуючи фінансово-економічні розрахунки, пов'язані з інвестуванням коштів, зростання і дисконтування вартості можуть відбуватися як за простими, так і за складними процентами. Перші, як правило, застосовуються в короткотерміновому інвестуванні, другі — в довгостроковому.

Простим процентом називається сума, яка нараховується за первісною (теперішньою) вартістю вкладу в кінці одною періоду платежу, тривалість якого обумовлена умовами інвестування коштів (місяць, квартал і т.н.).

Для розрахунку суми простого процента в процесі зростання вкладу використовується така формула:

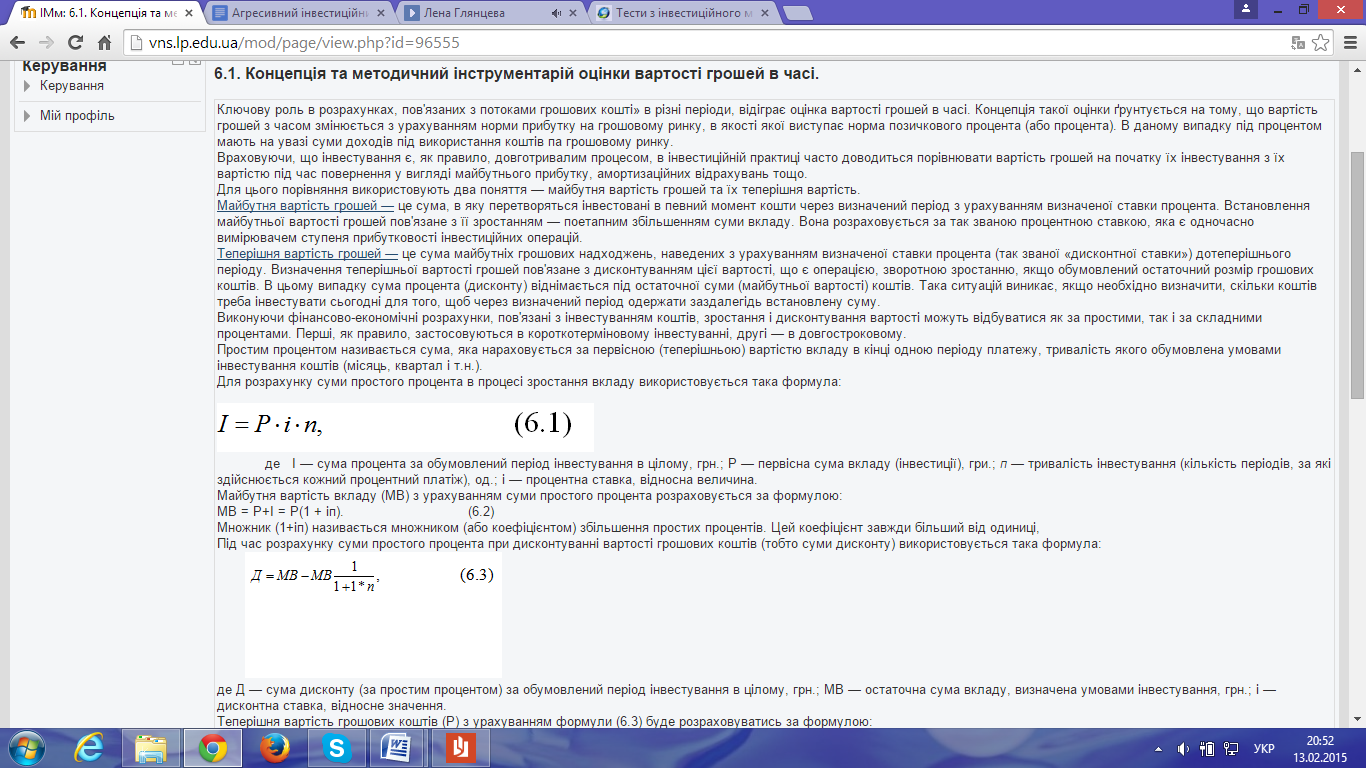
де І — сума процента за обумовлений період інвестування в цілому, грн.; Р — первісна сума вкладу (інвестиції), гри.; п — тривалість інвестування (кількість періодів, за які здійснюється кожний процентний платіж), од.; і — процентна ставка, відносна величина.
Майбутня вартість вкладу (МВ) з урахуванням суми простого процента розраховується за формулою:
МВ = Р+І = Р(1 + іп). (6.2)
Множник (1+іп) називається множником (або коефіцієнтом) збільшення простих процентів. Цей коефіцієнт завжди більший від одиниці,
Під час розрахунку суми простого процента при дисконтуванні вартості грошових коштів (тобто суми дисконту) використовується така формула:

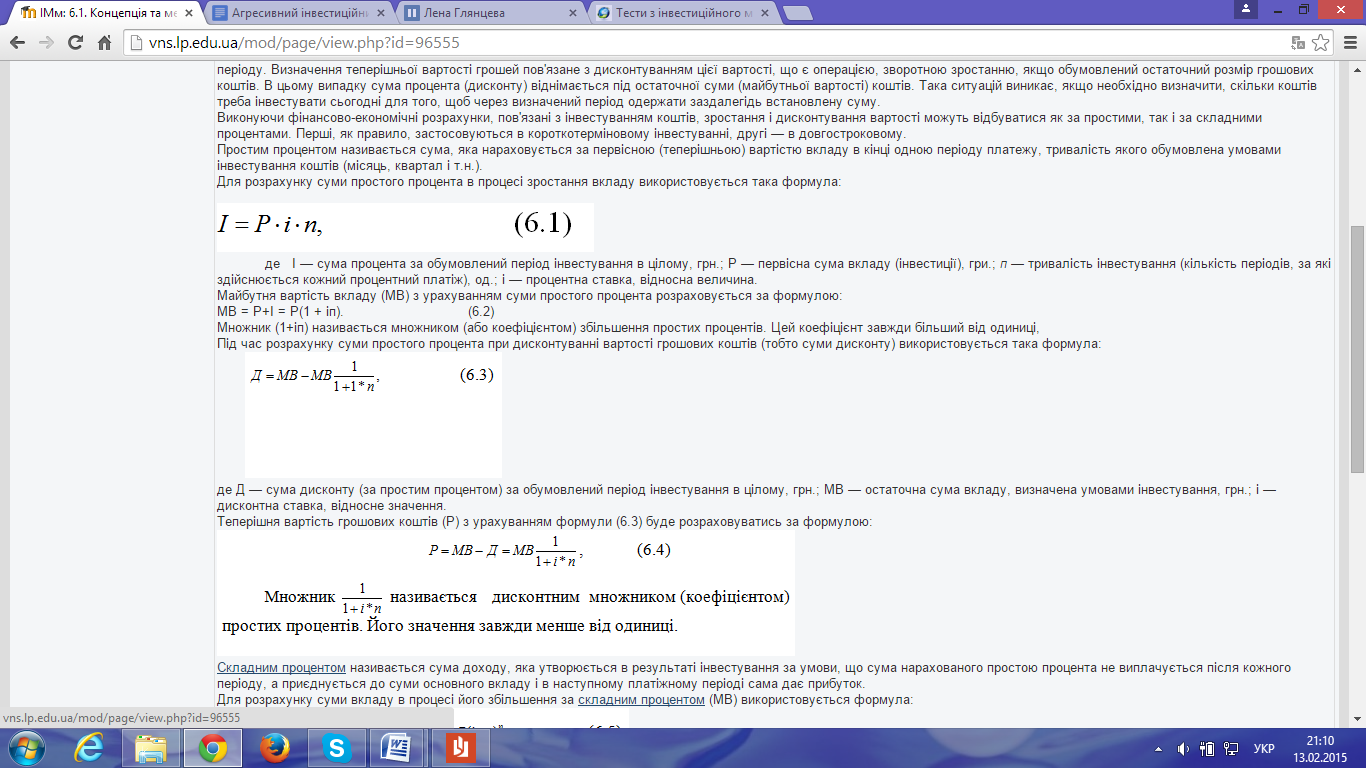
де Д — сума дисконту (за простим процентом) за обумовлений період інвестування в цілому, грн.; МВ — остаточна сума вкладу, визначена умовами інвестування, грн.; і — дисконтна ставка, відносне значення.
Теперішня вартість грошових коштів (Р) з урахуванням формули (6.3) буде розраховуватись за формулою:

Складним процентом називається сума доходу, яка утворюється в результаті інвестування за умови, що сума нарахованого простою процента не виплачується після кожного періоду, а приєднується до суми основного вкладу і в наступному платіжному періоді сама дає прибуток.
Для розрахунку суми вкладу в процесі його збільшення за складним процентом (МВ) використовується формула:

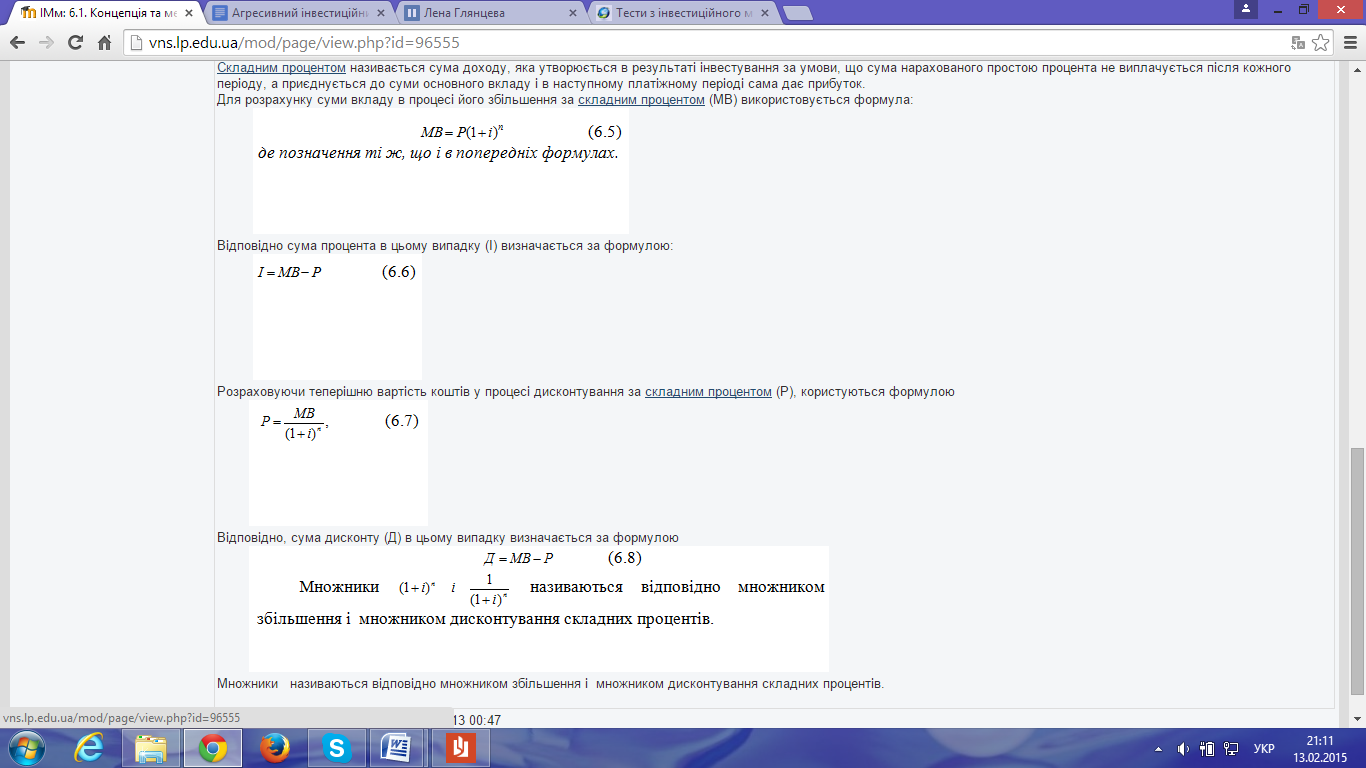
Відповідно сума процента в цьому випадку (І) визначається за формулою:

Розраховуючи теперішню вартість коштів у процесі дисконтування за складним процентом (Р), користуються формулою

Відповідно, сума дисконту (Д) в цьому випадку визначається за формулою

Множники називаються відповідно множником збільшення і множником дисконтування складних процентів.