Дифференциальных уравнений высоких порядков
Преобразуем дифференциальное уравнение (7.1) n-го порядка к системе n дифференциальных уравнений 1-го порядка
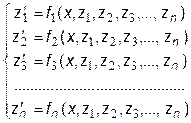
| (7.16) |
Запись уравнения (7.1) в виде системы (7.16) называется формой Коши. Начальные условия (7.1') при таком преобразовании выглядят так:
| z1(x0)=z1,0 ; z2(x0)=z2,0 ; z3(x0)=z3,0 ; . . . ; zn(x0)=zn,0 ; | (7.16’) |
Для примера преобразуем к форме Коши уравнение Бесселя :
.
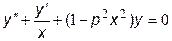Обозначим искомую функцию y(x) через z1(x), а ее первую производную - z2(x). Тогда получим систему уравнений первого порядка, эквивалентную исходному уравнению:
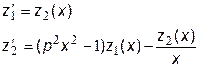
Вычислительный алгоритм "усовершенствованного" метода Эйлера для задачи Коши (7.16,7.16') выглядит аналогично (7.8):
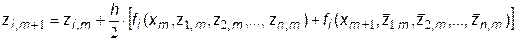
| (7.17) |
где i=1,2,...,n ;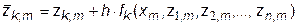 
; k=1,2,...,n .
Вычислительный алгоритм "модифицированного" метода Эйлера для задачи Коши (7.16,7.16') выглядит аналогично (7.12):
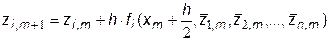
| (7.18) |
где i=1,2,...,n ;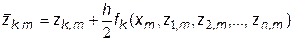 
; k=1,2,...,n .
Вычислительная схема метода Рунге-Кутта четвертого порядка для задачи Коши (7.16,7.16') имеет вид:
 ,
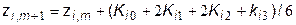| (7.19) |
| где | K i,0 = h fi(xm, z 1,m, z 2,m,..., z n,m), |
| K i,1 = h fi(xm+0.5h, z 1,m+0.5K1,0, z 2,m+0.5K2,0,..., z n,m+0.5Kn,0), | |
| K i,2 = h fi(xm+0.5h, z 1,m+0.5K1,1, z 2,m+0.5K2,1,..., z n,m+0.5Kn,1), | |
| K i,3 = h fi(xm+h, z 1,m+K1,2, z 2,m+K2,2,..., z n,m+Kn,2); | |
| i=1,2,...,n. |
Аналогичным образом обобщается на случай системы уравнений и схема (7.14) Кутта-Мерсона.
Дата добавления: 2015-02-16; просмотров: 1344;