ГОСЯ НА ВСТРЕЧНОМ ВОЛНЕНИИ. РЕШЕНИЕ УРАВНЕНИЙ

Левые части уравнений качки корабля, движущегося со скоростью 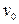, на тихой воде были получены в п. 4.2. Поскольку на волнении корабль качается с кажущейся частотой 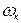(см. п. 3.5), в левых частях уравнений качки будут стоять те же выражения для сил и моментов, но зависящие от 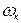, а в правых частях – выражения, полученные в п. 4.3. Коэффициенты правых частей не зависят от кажущейся частоты, так как они связаны с амплитудами волн, которые не должны меняться от присутствия волн. Тригонометрические функции будут зависеть от :

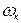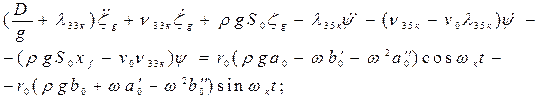(4.18)

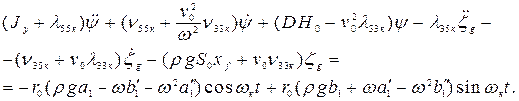(4.19)

Уравнения (4.18) и (4.19) являются обыкновенными линейными дифферен-циальными уравнениями 2-го порядка, неоднородными. Решения их ищутся в виде суммы 2-х решений: решения однородного уравнения (в правой части уравнения стоит 0) и решения неоднородного уравнения в форме правой части. Решения однородного уравнения быстро затухают, как мы это видели на примере бортовой качки на тихой воде, и остаются только решения в форме правых частей.

Правые части уравнений (4.18) и (4.19) можно представить в виде 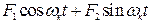, поэтому решения их ищем в виде:

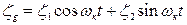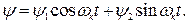и (4.20)

После определения производных

; ;

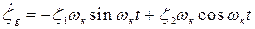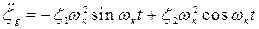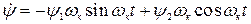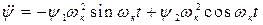; , (4.21) подстановки их в уравнения качки и уравнивания коэффициентов отдельно 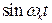при и при 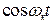в левой и правой частях получится система четырех алгебраических уравнений для определения четырех неизвестных величин 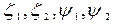. Они будут иметь вид:

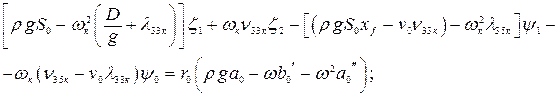
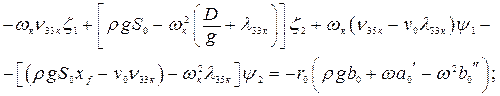
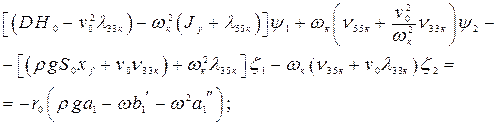
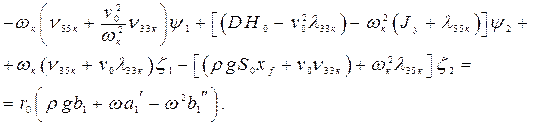(4.22)

Эта система уравнений решается каким-либо способом, например, с помощью определителей и т.д.

После нахождения 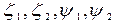можно построить положения корабля на волнении для ряда моментов времени, и таким образом, увидеть как у корабля заливается палуба или оголяется днище (на рис. 4.4 затопленные участки палубы заштрихованы). При этом можно решить, как расставить надстройки и фальшборт, чтобы исключить заливание палубы, а также решить другие вопросы обитаемости. При оголении днища можно рекомендовать снизить скорость хода корабля.

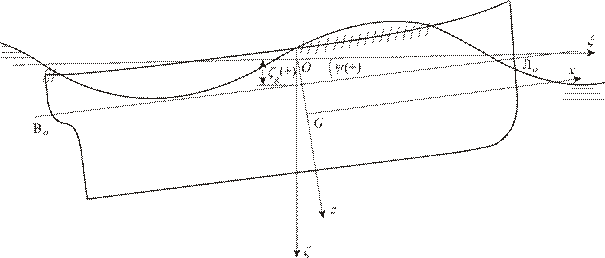
Рис. 4.4. К определению положения корабля на волнении