Критерий согласия Пирсона
Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H 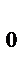 : генеральная совокупность распределена по определенному закону распределения, надо
: генеральная совокупность распределена по определенному закону распределения, надо
1) вычислить теоретические частоты,
2) найти наблюдаемое значение критерия по формуле 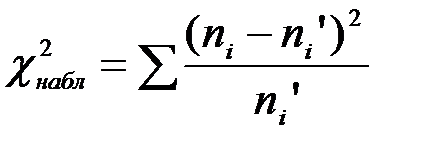 ,
,
где 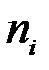 - фактические частоты,
- фактические частоты, 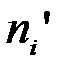 - теоретические частоты,
- теоретические частоты,
3) по таблице критических точек распределения 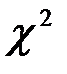 , по заданному уровню значимости
, по заданному уровню значимости  и числу степеней свободы k найти критическую точку
и числу степеней свободы k найти критическую точку 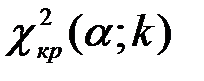 .
.
4) Если  - нет оснований отвергнуть нулевую гипотезу. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).
- нет оснований отвергнуть нулевую гипотезу. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).
Если 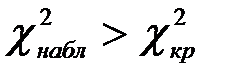 - нулевую гипотезу отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.
- нулевую гипотезу отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.
Замечание 1. Объем выборки должен быть достаточно велик, не менее 50. Интервалы, содержащие малочисленные эмпирические частоты ( 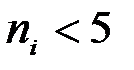 ), следует объединить, а частоты этих интервалов сложить.
), следует объединить, а частоты этих интервалов сложить.
Замечание 2. Число степеней свободы k определим по формуле k=l-r-1, где l – число частичных интервалов выборки; r – число параметров предполагаемого распределения, которые оценены по данным выборки. В частности, если предполагаемое распределение равномерное, то его можно задать двумя параметрами (например, число элементов и вероятность попадания в каждый из частичных интервалов), значит k=l-3. Если предполагаемое распределение нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому k=l-3. При проверке гипотезы о показательном распределении оценивают один параметр 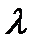 , значит k=l-2.
, значит k=l-2.
Дата добавления: 2015-02-13; просмотров: 1020;
