Корреляционный метод анализа связей

Корреляционный метод имеет две основные задачи:

1) обнаружить зависимость между факторным и результативным признаками и описать её форму с помощью уравнения регрессии;

2) установить меру тесноты связи между признаками (в какой мере вариация х обуславливает вариацию у).

Приступая к изучению корреляционной зависимости,следует помнить о том что, прежде всего, необходимо провести предварительный теоретический анализ. Он должен ответить на вопрос о том, существует ли такая связь вообще. Из истории статистики известно, что несоблюдение этого правила не раз приводило исследователей к курьезным результатам.

Предварительный теоретический анализ позволяет во многих случаях подсказать и форму связи (прямолинейная или более сложная), установить, является ли связь прямой пли обратной.

Сказанное выше означает, что каждый, кто прибегает к использованию метода корреляции, должен хорошо владеть не только данным методом, но и знанием предмета своего исследования.

Корреляционную связь, в которой есть только один признак-фактор и один признак-результат, именуют парной. Уравнение, выражающее такую связь, представляют какой-либо математической формулой прямой или кривых линий (гипербола, парабола и др.).

Для нахождения формы связи и описания ее в виде уравнения линии используют:

— группировку статистических данных;

— построение графика эмпирической линии.

Если точек очень много, то рассматривают не линию, а облако точек на графике корреляционного поля. В реальной практике не всегда удается достаточно уверенно по эмпирической линии установить форму линии связи. В этих случаях принимают несколько вариантов формы связи, по каждому из них делают расчеты и в конце дают оценку вариантов с помощью показателя тесноты связи. Вариант, в котором теснота связи оказалась наиболее высокой, принимается за наиболее верный.

Если форма связи выражается прямой линией, то уравнение регрессии имеет вид:

,

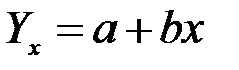где 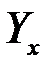- теоретическое значение,

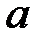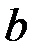и - параметры уравнения.

Параметр 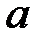экономической интерпретации не имеет. Параметр 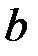называется коэффициентом регрессии, который показывает насколько изменится

результативный признак ( 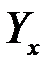) при изменении признака-фактора (x) на одну единицу.

Параметры уравнения 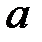и 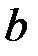находят из решения системы двух нормальных уравнений:

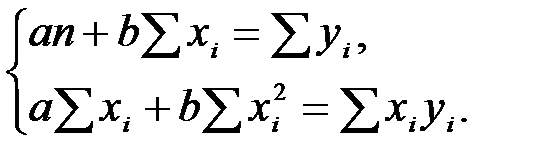
Решая эту систему относительно параметров a и b, получим:

,

.

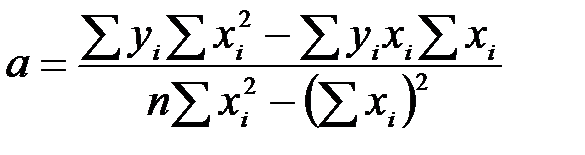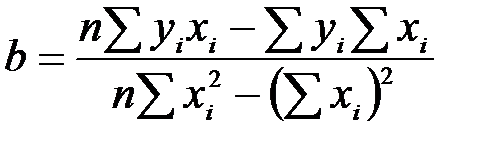Уравнение регрессии можно использовать для прогнозирования, если связь между факторным и результативным признаками достаточно тесная.

В случае прямолинейной формы связи теснота может быть измерена линейным коэффициентом корреляции по формуле:

.

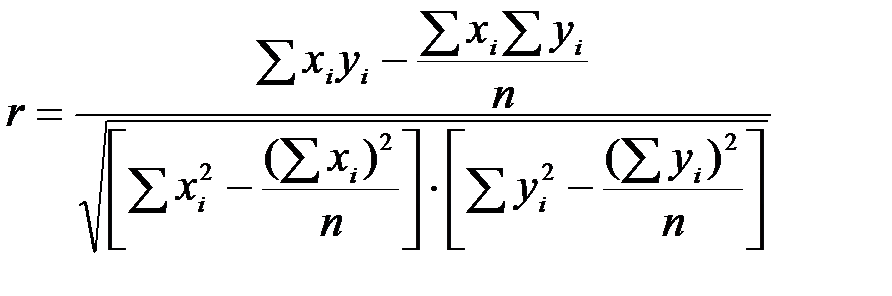Коэффициент корреляции может находится в пределах от 0 (связь отсутствует) до 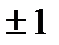(связь полная). Знак «+» указывает на прямую, а знак «–» на обратную связь.

Существуют способы оценки тесноты связи. В частности, по таблице Чэддока тесноту связи определяют следующим образом (см. табл. 5.1):

Таблица 5.1

В упрощенном виде считают, что если коэффициент (по модулю) составляет от 0,1 до 0,3 – связь слабая, от 0,3 до 0,7 – средняя, от 0,7 и выше – тесная.