ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА

Статистической гипотезойназывается предположение о свойстве генеральной совокупности, которое можно проверить, опираясь на данные выборки.

Гипотезы о параметрах генеральной совокупности называют параметрическими, о распределениях – непараметрическими.

Гипотеза о том, что две величины или что две совокупности, сравниваемые по одному или нескольким признаком, не отличаются, называют нулевой (основной) гипотезой. Она обозначается H 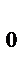. При этом предполагается, что действительное различие сравниваемых величин равно нулю, а выявленное по данным отличие от нуля носит случайный характер.

Конкурирующей (альтернативной) называют гипотезу H 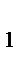, которая противоречит нулевой.

Статистическим критерием называют определенное правило, устанавливающее условия при которых проверяемую нулевую гипотезу следует либо отклонить, либо не отклонить.

Проверка статистических гипотез складывается из следующих этапов:

1. Формулируется в виде статистической гипотезы задача исследования.

2. Выбирается статистическая характеристика гипотезы.

3. Выбираются нулевая и конкурирующая гипотезы на основе анализа возможных ошибочных решений и их последствий.

4. Определяются область допустимых значений, критическая область, а так же критическое значение статистического критерия по соответствующей таблице.

5. Вычисляется фактическое значение статистического критерия.

6. Проверяется испытуемая гипотеза на основе сравнения фактического и критического значения критерия и в зависимости от результатов проверки гипотеза либо отклоняется, либо не отклоняется.

При проверки гипотез по одному из критериев возможны два ошибочных решения:

1) неправильное отклонение нулевой гипотезы: ошибка 1-го рода;

2) неправильное принятие нулевой гипотезы: ошибка 2-го рода.

Правильное решение может быть принято также в двух случаях:

1) гипотеза принимается, причем и в действительности она правильная;

2) гипотеза отвергается, причем и в действительности она неверна.

Вероятность совершить ошибку первого рода принято обозначать через 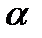, ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01.

Критической областью называется область, попадание значения статистического критерия в которую приводит к отклонению H 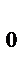. Вероятность попадания значения критерия в эту область равна принятому уровню значимости.

Область допустимых значений дополняет критическую область. Если значение критерия попадает в область допустимых значений, это свидетельствует о том, что выдвинутая гипотеза H 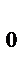не противоречит фактическим данным (H 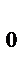не отклоняется).

Точки, разделяющие критическую область и область допустимых значений, называются критическими точками или границами критической области. В зависимости от формулировки альтернативной гипотезы критическая область может быть двухсторонняя или односторонняя (левосторонняя либо правосторонняя).

Критические точки находятся по таблицам приложений в соответствии с используемым критерием согласия (Пирсона, Стьюдента, Фишера и т.д.).

Наблюдаемое значение критерия вычисляется по статистическим данным. Если оно попадает в критическую область, то нулевая гипотеза отклоняется. Если наблюдаемое значение критерия попадает в область допустимых значений, то нет оснований отклонить нулевую гипотезу.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Гипотезы о распределениях заключаются в том, что выдвигается предположение о том, что распределение в генеральной совокупности подчиняется какому-то определенному закону. Проверка гипотезы состоит в том, чтобы на основании сравнения фактических (эмпирических) частот с предполагаемыми (теоретическими) частотами сделать вывод о соответствии фактического распределения гипотетическому распределению.